Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Pittel, B
1987.
Linear probing: The probable largest search time grows logarithmically with the number of records.
Journal of Algorithms,
Vol. 8,
Issue. 2,
p.
236.
Pittel, B.
1988.
A random graph with a subcritical number of edges.
Transactions of the American Mathematical Society,
Vol. 309,
Issue. 1,
p.
51.
Regnier, M.
1988.
Trie hashing analysis.
p.
377.
Aldous, David
and
Shields, Paul
1988.
A diffusion limit for a class of randomly-growing binary trees.
Probability Theory and Related Fields,
Vol. 79,
Issue. 4,
p.
509.
Szpankowski, Wojciech
1988.
Some results on V-ary asymmetric tries.
Journal of Algorithms,
Vol. 9,
Issue. 2,
p.
224.
Szpankowski, Wojciech
1989.
Algorithms and Data Structures.
Vol. 382,
Issue. ,
p.
206.
Regnier, M.
and
Jacquet, P.
1989.
New results on the size of tries.
IEEE Transactions on Information Theory,
Vol. 35,
Issue. 1,
p.
203.
Pittel, B
and
Rubin, H
1990.
How many random questions are necessary to identify n distinct objects?.
Journal of Combinatorial Theory, Series A,
Vol. 55,
Issue. 2,
p.
292.
VITTER, Jeffrey Scott
and
FLAJOLET, Philippe
1990.
Algorithms and Complexity.
p.
431.
Aoe, Jun-ichi
1990.
A compendium of key search references.
ACM SIGIR Forum,
Vol. 24,
Issue. 3,
p.
26.
Gupta, Vijay K.
Mesa, Oscar J.
and
Waymire, E.
1990.
Tree-dependent extreme values: the exponential case.
Journal of Applied Probability,
Vol. 27,
Issue. 01,
p.
124.
Szpankowski, W.
1991.
A typical behavior of some data compression schemes.
p.
247.
Szpankowski, Wojciech
1991.
On the height of digital trees and related problems.
Algorithmica,
Vol. 6,
Issue. 1-6,
p.
256.
Jacquet, Philippe
and
Szpankowski, Wojciech
1991.
Algorithms and Data Structures.
Vol. 519,
Issue. ,
p.
228.
Jacquet, P.
and
Szpankowski, W.
1991.
Analysis of digital tries with Markovian dependency.
IEEE Transactions on Information Theory,
Vol. 37,
Issue. 5,
p.
1470.
Szpankowski, Wojciech
1991.
A characterization of digital search trees from the successful search viewpoint.
Theoretical Computer Science,
Vol. 85,
Issue. 1,
p.
117.
Devroye, Luc
1992.
A note on the probabilistic analysis of patricia trees.
Random Structures & Algorithms,
Vol. 3,
Issue. 2,
p.
203.
Devroye, Luc
Szpankowski, Wojciech
and
Rais, Bonita
1992.
A Note on the Height of Suffix Trees.
SIAM Journal on Computing,
Vol. 21,
Issue. 1,
p.
48.
Louchard, G.
1993.
TAPSOFT'93: Theory and Practice of Software Development.
Vol. 668,
Issue. ,
p.
717.
Rais, Bonita
Jacquet, Philippe
and
Szpankowski, Wojciech
1993.
Limiting Distribution for the Depth in PATRICIA Tries.
SIAM Journal on Discrete Mathematics,
Vol. 6,
Issue. 2,
p.
197.
 of paths in T. The tree tn is obtained by cutting each
of paths in T. The tree tn is obtained by cutting each 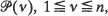 , at the first node such that at most σ paths out of
, at the first node such that at most σ paths out of 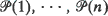 , pass through it. Denote by Hn the length of the longest path, hn the length of the shortest path, and Ln the length of the randomly chosen path in tn. It is shown that, in probability, Hn – logan = O(1), hn – logb (n/log n) = 0(1), (or hn – logb (n/log log n) = O(1)), and that
, pass through it. Denote by Hn the length of the longest path, hn the length of the shortest path, and Ln the length of the randomly chosen path in tn. It is shown that, in probability, Hn – logan = O(1), hn – logb (n/log n) = 0(1), (or hn – logb (n/log log n) = O(1)), and that  is asymptotically normal. The parameters a, b, c depend on the distribution of ω and, in case of a, also on σ. These estimates describe respectively the worst, the best and the typical case behavior of a ‘trie’ search algorithm for a dictionary-type information retrieval system, with σ being the capacity of a page.
is asymptotically normal. The parameters a, b, c depend on the distribution of ω and, in case of a, also on σ. These estimates describe respectively the worst, the best and the typical case behavior of a ‘trie’ search algorithm for a dictionary-type information retrieval system, with σ being the capacity of a page.
