Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T05:11:52.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Perturbation theory for Markov reward processes with applications to queueing systems

Published online by Cambridge University Press:  01 July 2016

Nico M. Van Dijk  and
Martin L. Puterman
Nico M. Van Dijk*
Affiliation:
Free University, Amsterdam
Martin L. Puterman*
Affiliation:
University of British Columbia
*
∗Postal address: Faculty of Economical Sciences and Econometrics, Free University, P.O-Box 7161, 1007 MC Amsterdam, The Netherlands.
∗∗Postal address: Faculty of Commerce and Business Administration, The University of British Columbia, 2053 Main Mall, Vancouver, B.C. Canada V6T 1Y8.
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the effect of perturbations in the data of a discrete-time Markov reward process on the finite-horizon total expected reward, the infinite-horizon expected discounted and average reward and the total expected reward up to a first-passage time. Bounds for the absolute errors of these reward functions are obtained. The results are illustrated for a finite as well as infinite queueing systems (M/M/1/S and ). 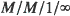Extensions to Markov decision processes and other settings are discussed.

Keywords

PERTURBATIONSREWARD FUNCTIONSMEAN FIRST-PASSAGE TIMESM/M/1/S QUEUESMARKOV DECISION PROCESSES
Type
Research Article
Information
Advances in Applied Probability , Volume 20 , Issue 1 , March 1988 , pp. 79 - 98
Copyright
Copyright © Applied Probability Trust 1988 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was supported in part by the National Sciences and Engineering Research Council of Canada Grant A-5527.

References

[1] Çinlar, E. (1975) Introduction to Stochastic Processes. Prentice-Hall, Englewood Cliffs, NJ.Google Scholar
[2] Hinderer, K. (1978) On approximate solutions of finite-stage dynamic programs. Dynamic Programming and its Application, ed Puterman, M., Academic Press, New York, 289–318.CrossRefGoogle Scholar
[3] Horduk, A. (1974) Dynamic Programming and Markov Potential Theory. Mathematical Centre Tract 51, Amsterdam.Google Scholar
[4] Jensen, A. (1953) Markov chains as an aid in the study of Markov processes. Skand. Aktuartidskr. 36, 87–91.Google Scholar
[5] Kemeny, J. G. and Snell, J. L. (1960) Finite Markov Chains. Van Nostrand, Princeton, NJ.Google Scholar
[6] Kemeny, J. G., Snell, J. L. and Knapp, A. W. (1966) Denumerable Markov Chains. Van Nostrand, Princeton, NJ.Google Scholar
[7] Meyer, C. D. Jr (1980) The condition of a finite Markov chain and perturbation bounds for the limiting probabilities. SIAM J. Alg. Discrete Methods 1, 273–283.CrossRefGoogle Scholar
[8] Ralston, A. (1965) A First Course in Numerical Analysis. McGraw-Hill, New York.Google Scholar
[9] Ross, S. M. (1970) Applied Probability Models with Optimization Application. Holden Day, San Francisco.Google Scholar
[10] Schweitzer, P. J. (1968) Perturbation theory and finite Markov chains. J. Appl. Prob. 5, 401–413.Google Scholar
[11] Van Dijk, N. M. (1984) Controlled Markov Process: Time Discretization. CWI Tract 11, Amsterdam.Google Scholar
[12] Whitt, W. (1978) Approximations of dynamic programs, I. Math. Operat. Res. 3, 231–243.CrossRefGoogle Scholar
[13] White, C. C. Iii and El Dieb, H. K. (1986) Parameter imprecisions in finite state, finite action dynamic programs. Operat. Res. 34, 120–129.CrossRefGoogle Scholar
[14] Widder, D. V. (1946) The Laplace Transform. Princeton University Press. Princeton, NJ.Google Scholar