Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T03:42:34.262Z Has data issue: false hasContentIssue false
  • English
  • Français

Poisson and extreme value limit theorems for Markov random fields

Published online by Cambridge University Press:  01 July 2016

Simeon M. Berman
Simeon M. Berman*
Affiliation:
Courant Institute of Mathematical Sciences
*
∗Postal address: Courant Institute of Mathematical Sciences, New York University, 251 Mercer Street, New York, NY 10012, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Xt, 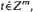be a Markov random field assuming values in RM. Let In be a rectangular box in Zm with its center at 0 and corner points with coordinates ±n. Let (An) be a sequence of measurable subsets of RM such that 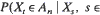neighborhood of t) → 0, for n → ∞; and let fn(x) be the indicator of An. Under appropriate conditions on the nearest-neighbor distributions of (Xt), the conditional distribution of 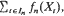given the values of Xs, for s on the boundary of In, converges to the Poisson distribution. An immediate application is an extreme value limit theorem for a real-valued Markov random field.

Keywords

STATIONARITYMIXINGEXTREME VALUESPOISSON LIMIT
Type
Research Article
Information
Advances in Applied Probability , Volume 19 , Issue 1 , March 1987 , pp. 106 - 122
Copyright
Copyright © Applied Probability Trust 1987 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This paper represents results obtained at the Courant Institute of Mathematical Sciences, New York University, under the sponsorship of the U.S. Army Research Office, Grant number DAAG-29-85-K-0146, and the National Science Foundation, Grant DMS 85 01512.

References

1. Bartlett, M. S. (1975) The Statistical Analysis of Spatial Pattern. Chapman and Hall, London.Google Scholar
2. Berman, S. M. (1964) Limit theorems for the maximum term in stationary sequences. Ann. Math. Statist. 35, 502–516.CrossRefGoogle Scholar
3. Berman, S. M. (1984) Limiting distribution of sums of non-negative stationary random variables. Ann. Inst. Statist. Math. 36, 301–321.Google Scholar
4. Besag, J. (1974) Spatial interaction and the statistical analysis of lattice systems. J. R. Statist. Soc. B36, 192–236.Google Scholar
5. Chay, S. C. (1972) On quasi-Markov random fields. J. Multivariate Anal. 2, 14–76.CrossRefGoogle Scholar
6. Dobrushin, R. L. (1968) The description of a random field by means of conditional probabilities and conditions of its regularity. Theory Prob. Appl. 13, 197–224.CrossRefGoogle Scholar
7. Dobrushin, R. L. (1970) Prescribing a system of random variables by conditional distributions. Theory Prob. Appl. 15, 458–486.CrossRefGoogle Scholar
8. Dobrushin, R. L. and Sinai, Ya. G., (Ed) (1980) Multicomponent Random Systems. Marcel Dekker, New York.Google Scholar
9. Galambos, J. (1978) The Asymptotic Theory of Extreme Order Statistics. Wiley, New York.Google Scholar
10. Gnedenko, B. V. (1943) Sur la distribution limite du terme maximum d&une série aléatoire. Ann. Math. 44, 423–453.CrossRefGoogle Scholar
11. Grimmett, G. R. (1973) A theorem about random fields. Bull. London Math. Soc. 5, 81–84.Google Scholar
12. De Haan, L. (1970) On Regular Variation and its Application to the Weak Convergence of Sample Extremes. Mathematical Centre Tracts 32, Amsterdam.Google Scholar
13. Kindermann, R. and Snell, J. L. (1980) Markov Random Fields and their Applications. Vol. 1 of Contemporary Mathematics, American Math. Soc., Providence 1980.CrossRefGoogle Scholar
14. Leadbetter, M. R., Lindgren, G., and Rootzen, H. (1983) Extremes and Related Properties of Random Sequences and Processes. Springer-Verlag, New York.CrossRefGoogle Scholar
15. Loève, M. (1978) Probability Theory, Fourth Edition Vol. II, Springer-Verlag, New York.Google Scholar
16. Nahapetian, B. S. (1980) The central limit theorem for random fields with mixing property, In Multicomponent Random Systems, Ed. Dobrushin, R. L. and Sinai, YA. G. Marcel Dekker, New York. 531–547.Google Scholar
17. Rosenfeld, A., (Ed) (1981) Image Modeling. Academic Press, New York.Google Scholar
18. Rozanov, Yu. A. (1967) On Gaussian fields with given conditional distributions. Theory Prob. Appl. 12, 381–391.Google Scholar
19. Scheffé, H. (1947) A useful convergence theorem for probability distributions. Ann. Math. Statist. 18, 434–438.CrossRefGoogle Scholar