Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sumita, Ushio
and
Shanthikumar, J. George
1985.
A class of correlated cumulative shock models.
Advances in Applied Probability,
Vol. 17,
Issue. 02,
p.
347.
Shanthikumar, J.George
1986.
First failure time of dependent parallel systems with safety periods.
Microelectronics Reliability,
Vol. 26,
Issue. 5,
p.
955.
Karasu, Izi
and
Özekici, Süleyman
1989.
NBUE and NWUE properties of increasing Markov processes.
Journal of Applied Probability,
Vol. 26,
Issue. 04,
p.
827.
Özekici, S.
and
Günlük, N. O.
1992.
Maintenance of a device with age-dependent exponential failures.
Naval Research Logistics,
Vol. 39,
Issue. 5,
p.
699.
Lam, C. Y. Teresa
1992.
New better than used in expectation processes.
Journal of Applied Probability,
Vol. 29,
Issue. 01,
p.
116.
Pellerey, Franco
and
Shaked, Moshe
1993.
Stochastic Comparison of Some Wear Processes.
Probability in the Engineering and Informational Sciences,
Vol. 7,
Issue. 3,
p.
421.
Shaked, Moshe
Shanthikumar, J. George
and
Zhu, Haolong
1993.
Discrete repairable reliability systems.
Naval Research Logistics,
Vol. 40,
Issue. 6,
p.
769.
Li, Haijun
and
Shaked, Moshe
1995.
On the first passage times for Markov processes with monotone convex transition kernels.
Stochastic Processes and their Applications,
Vol. 58,
Issue. 2,
p.
205.
Pellerey, Franco
and
Shaked, Moshe
1996.
Stochastic comparison of processes generated by random interruptions of monotone functions and related results.
Lifetime Data Analysis,
Vol. 2,
Issue. 1,
p.
91.
Berenhaut, Kenneth S.
and
Lund, Robert
2001.
Geometric renewal convergence rates from hazard rates.
Journal of Applied Probability,
Vol. 38,
Issue. 1,
p.
180.
Berenhaut, Kenneth S.
and
Lund, Robert
2001.
Geometric renewal convergence rates from hazard rates.
Journal of Applied Probability,
Vol. 38,
Issue. 01,
p.
180.
Kijima, Masaaki
Li, Haijun
and
Shaked, Moshe
2001.
Stochastic Processes: Theory and Methods.
Vol. 19,
Issue. ,
p.
471.
Belzunce, Félix
Ortega, Eva-María
and
Ruiz, José M.
2002.
On ageing properties of first-passage times of increasing Markov processes.
Advances in Applied Probability,
Vol. 34,
Issue. 01,
p.
241.
Shaked, M.
and
Li, H.
2004.
Encyclopedia of Statistical Sciences.
Griffith, William S.
2004.
Encyclopedia of Statistical Sciences.
Shaked, M.
and
Li, H.
2005.
Encyclopedia of Statistical Sciences.
Griffith, William S.
2005.
Encyclopedia of Statistical Sciences.
Griffith, William S.
2014.
Wiley StatsRef: Statistics Reference Online.
Shaked, M.
and
Li, H.
2014.
Wiley StatsRef: Statistics Reference Online.
Griffith, William S.
2015.
Wiley StatsRef: Statistics Reference Online.
p.
1.

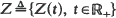 with
with 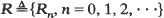 with
with  . In this paper we present sufficient conditions under which (
. In this paper we present sufficient conditions under which (