Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Molchanov, Ilya
2017.
Theory of Random Sets.
Vol. 87,
Issue. ,
p.
1.
Molchanov, Ilya
2017.
Theory of Random Sets.
Vol. 87,
Issue. ,
p.
225.
Bianchi, Gabriele
Gardner, Richard J.
and
Gronchi, Paolo
2017.
Symmetrization in geometry.
Advances in Mathematics,
Vol. 306,
Issue. ,
p.
51.
Bianchi, Gabriele
and
Gronchi, Paolo
2023.
Convex Geometry.
Vol. 2332,
Issue. ,
p.
233.
Ulivelli, Jacopo
2023.
Convergence properties of symmetrization processes.
Advances in Applied Mathematics,
Vol. 146,
Issue. ,
p.
102484.
Ulivelli, Jacopo
2023.
Generalization of Klain’s theorem to Minkowski symmetrization of compact sets and related topics.
Canadian Mathematical Bulletin,
Vol. 66,
Issue. 1,
p.
124.

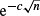 with
with 