Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T06:36:47.039Z Has data issue: false hasContentIssue false
  • English
  • Français

Random transceiver networks

Part of: Special processes Equilibrium statistical mechanics

Published online by Cambridge University Press:  01 July 2016

Paul Balister ,
Béla Bollobás  and
Mark Walters
Paul Balister*
Affiliation:
University of Memphis
Béla Bollobás*
Affiliation:
University of Memphis
Mark Walters*
Affiliation:
University of Cambridge
*
∗ Postal address: University of Memphis, Department of Mathematics, Dunn Hall, 3725 Noriswood, Memphis, TN 38152, USA.
∗∗ Current address: Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, Cambridge, CB3 0WB, UK.
∗∗∗ Current address: School of Mathematical Sciences, Queen Mary, University of London, Mile End Road, London E1 4NS, UK. Email address: m.walters@qmul.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider randomly scattered radio transceivers in ℝd, each of which can transmit signals to all transceivers in a given randomly chosen region about itself. If a signal is retransmitted by every transceiver that receives it, under what circumstances will a signal propagate to a large distance from its starting point? Put more formally, place points {xi} in ℝd according to a Poisson process with intensity 1. Then, independently for each xi, choose a bounded region Axi from some fixed distribution and let 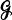be the random directed graph with vertex set 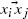whenever xj ∈ xi + Axi. We show that, for any 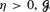will almost surely have an infinite directed path, provided the expected number of transceivers that can receive a signal directly from xi is at least 1 + η, and the regions xi + Axi do not overlap too much (in a sense that we shall make precise). One example where these conditions hold, and so gives rise to percolation, is in ℝd, with each Axi a ball of volume 1 + η centred at xi, where η → 0 as d → ∞. Another example is in two dimensions, where the Axi are sectors of angle ε γ and area 1 + η, uniformly randomly oriented within a fixed angle (1 + ε)θ. In this case we can let η → 0 as ε → 0 and still obtain percolation. The result is already known for the annulus, i.e. that the critical area tends to 1 as the ratio of the radii tends to 1, while it is known to be false for the square (l∞) annulus. Our results show that it does however hold for the randomly oriented square annulus.

Keywords

Random networkrandom geometric graphpercolation

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 82B43: Percolation
Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 41 , Issue 2 , June 2009 , pp. 323 - 343
Copyright
Copyright © Applied Probability Trust 2009 

Footnotes

Research supported by NSF grant EIA-0130352.

Research supported in part by NSF grants DMS-0505550, CNS-0721983, CCF-0728928, and EIA-0130352, and an ARO grant W911NF-06-1-0076.

References

Athreya, K. and Ney, P. (1972). Branching Processes. Springer, New York.CrossRefGoogle Scholar
Balister, P., Bollobás, B. and Stacey, A. (1994). Improved upper bounds for the critical probability of oriented percolation in two dimensions. Random Structures Algorithms 5, 573–589.CrossRefGoogle Scholar
Balister, P., Bollobás, B. and Walters, M. (2004). Continuum percolation with steps in an annulus. Ann. Appl. Prob. 14, 1869–1879.CrossRefGoogle Scholar
Balister, P., Bollobás, B. and Walters, M. (2005). Continuum percolation with steps in the square and the disc. Random Structures Algorithms 26, 392–403.CrossRefGoogle Scholar
Bollobás, B. (2001). Random Graphs (Camb. Stud. Adv. Math. 73), 2nd edn. Cambridge University Press.CrossRefGoogle Scholar
Flaxman, A., Frieze, A. and Upfal, E. (2004). Efficient communication in an ad-hoc network. J. Algorithms 52, 1–7.CrossRefGoogle Scholar
Franceschetti, M. et al. (2005). Continuum percolation with unreliable and spread-out connections. J. Statist. Phys. 118, 721–734.CrossRefGoogle Scholar
Grimmett, G. (1999). Percolation (Fundamental Principles Math. Sci. 321), 2nd edn. Springer, Berlin.CrossRefGoogle Scholar
Meester, R. and Roy, R. (1996). Continuum Percolation (Camb. Tracts Math. 119). Cambridge University Press.CrossRefGoogle Scholar
Quintanilla, J., Torquato, S. and Ziff, R. M. (2000). Efficient measurement of the percolation threshold for fully penetrable discs. J. Phys. A 33, L399–L407.CrossRefGoogle Scholar