Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T00:47:27.682Z Has data issue: false hasContentIssue false
  • English
  • Français

Rates of convergence for random approximations of convex sets

Part of: General convexity

Published online by Cambridge University Press:  01 July 2016

Lutz Dümbgen  and
Günther Walther
Lutz Dümbgen*
Affiliation:
Universität Heidelberg
Günther Walther*
Affiliation:
Stanford University
*
∗ Postal address: Institut für Angewandte Mathematik, Universität Heidelberg, Im Neuenheimer Feld 294, D-69120 Heidelberg, Germany. E-mail: lutz@statlab.uni-heidelberg.de
∗∗ Postal address: Department of Statistics, Stanford University, Stanford CA 94305, USA. e-mail: walther@playfair.stanford.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

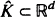The Hausdorff distance between a compact convex set K ⊂ ℝd and random sets is studied. Basic inequalities are derived for the case of 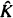being a convex subset of 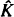K. If applied to special sequences of such random sets, these inequalities yield rates of almost sure convergence. With the help of duality considerations these results are extended to the case of being the intersection of a random family of halfspaces containing K.

Keywords

CONVEX SETDUALITYPACKING NUMBERSPOLAR SETPROBABILITY INEQUALITYRATE OF CONVERGENCE

MSC classification

Secondary: 52A22: Random convex sets and integral geometry
Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 28 , Issue 2 , June 1996 , pp. 384 - 393
Copyright
Copyright © Applied Probability Trust 1996 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barany, I. (1989) Intrinsic volumes and f-vectors of random polytopes. Math. Ann. 285, 671–699.CrossRefGoogle Scholar
Burago, Y. D. and Zalgaller, V. A. (1988) Geometric Inequalities. Springer, New York.Google Scholar
Federer, H. (1969) Geometric Measure Theory. Springer, Berlin.Google Scholar
Pollard, D. (1990) Empirical Processes: Theory and Applications. (NSF-CBMS Regional Conf. Series Prob. Statist. 2) IMS, Hayward, CA.Google Scholar
Schneider, R. (1988) Random approximation of convex sets. J. Microsc. 151, 211–227.Google Scholar
Schneider, R. (1993) Convex Bodies: The Brunn-Minkowski Theory. Cambridge University Press, Cambridge.Google Scholar
Small, C. G. (1991) Reconstructing convex bodies from random projected images. Canadian J. Statist. 19, 341–347.Google Scholar
Weil, W. and Wieacker, J. A. (1993) Stochastic Geometry. In Handbook of Convex Geometry, Vol. B. ed. Gruber, P. M. and Wills, J. M., pp. 1391–1438. Elsevier, Amsterdam.Google Scholar