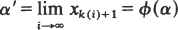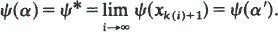Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Seneta, E.
1982.
Entropy and martingales in Markov chain models.
Journal of Applied Probability,
Vol. 19,
Issue. A,
p.
367.
Seneta, E.
1986.
An inequality from genetics.
Advances in Applied Probability,
Vol. 18,
Issue. 03,
p.
860.

 where
where  say). Let Φ (mapping
say). Let Φ (mapping