Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T19:47:17.802Z Has data issue: false hasContentIssue false
  • English
  • Français

Selecting the last consecutive record in a record process

Part of: Stochastic processes Special processes Sequential methods

Published online by Cambridge University Press:  01 July 2016

Shoou-Ren Hsiau
Shoou-Ren Hsiau*
Affiliation:
National Changhua University of Education
*
∗ Postal address: Department of Mathematics, National Changhua University of Education, No. 1, Jin-De Road, Changhua 500, Taiwan, R.O.C. Email address: srhsiau@cc.ncue.edu.tw
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that I1, I2,… is a sequence of independent Bernoulli random variables with E(In) = λ/(λ + n − 1), n = 1, 2,…. If λ is a positive integer k, {In}n≥1 can be interpreted as a k-record process of a sequence of independent and identically distributed random variables with a common continuous distribution. When In−1In = 1, we say that a consecutive k-record occurs at time n. It is known that the total number of consecutive k-records is Poisson distributed with mean k. In fact, for general 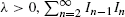is Poisson distributed with mean λ. In this paper, we want to find an optimal stopping time τλ which maximizes the probability of stopping at the last n such that In−1In = 1. We prove that τλ is of threshold type, i.e. there exists a tλ ∈ ℕ such that τλ = min{n | n ≥ tλ, In−1In = 1}. We show that tλ is increasing in λ and derive an explicit expression for tλ. We also compute the maximum probability Qλ of stopping at the last consecutive record and study the asymptotic behavior of Qλ as λ → ∞.

Keywords

Optimal stoppingthreshold typeconsecutive recordmonotone stopping rulerecord process

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory
Secondary: 62L15: Optimal stopping 60K99: None of the above, but in this section
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 42 , Issue 3 , September 2010 , pp. 739 - 760
Copyright
Copyright © Applied Probability Trust 2010 

References

Arratia, R., Barbour, A. D. and Tavaré, S. (1992). Poisson process approximations for the Ewens sampling formula. Ann. Appl. Prob. 2, 519–535.Google Scholar
Bruss, F. T. (2000). Sum the odds to one and stop. Ann. Prob. 28, 1384–1391.Google Scholar
Bruss, F. T. and Louchard, G. (2003). Optimal stopping on patterns in strings generated by independent random variables. J. Appl. Prob. 40, 49–72.CrossRefGoogle Scholar
Bruss, F. T. and Paindaveine, D. (2000). Selecting a sequence of last successes in independent trials. J. Appl. Prob. 37, 389–399.Google Scholar
Chern, H.-H., Hwang, H.-K. and Yeh, Y.-N. (2000). Distribution of the number of consecutive records. Random Structures Algorithms 17, 169–196.Google Scholar
Chow, Y. S. and Robbins, H. (1961). A martingale system theorem and applications. In Proc. 4th Berkeley Symp. Math. Statist. Prob., Vol. 1, University of California Press, Berkeley, CA, pp. 93–104.Google Scholar
Chow, Y.-S., Robbins, H. and Siegmund, D. (1971). Great Expectations: the Theory of Optimal Stopping. Houghton Mifflin, Boston, MA.Google Scholar
Csörgö, S. and Wu, W. B. (2000). On sums of overlapping products of independent Bernoulli random variables. Ukraï n. Mat. Zh. 52, 1304–1309. English translation: Ukrainian Math. J. 52, 1496–1503.Google Scholar
Dynkin, E. B. (1963). Optimal choice of the stopping moment of a Markov process. Dokl. Akad. Nauk SSSR 150, 238–240 (in Russian).Google Scholar
Hahlin, L. O. (1995). Double records. Res. Rep. 1995: 12, Department of Mathematics, Uppsala University.Google Scholar
Holst, L. (2007). Counts of failure strings in certain Bernoulli sequences. J. Appl. Prob. 44, 824–830.Google Scholar
Hsiau, S.-R. (2007). Stopping at the last renewal up to a terminal time. Statist. Sinica 17, 725–733.Google Scholar
Hsiau, S.-R. and Yang, J.-R. (2002). Selecting the last success in Markov-dependent trials. J. Appl. Prob. 39, 271–281.Google Scholar
Joffe, A., Marchand, É., Perron, F. and Popadiuk, P. (2004). On sums of products of Bernoulli variables and random permutations. J. Theoret. Prob. 17, 285–292.Google Scholar
Mori, T. F. (2001). On the distribution of sums of overlapping products. Acta Sci. Math. 67, 833–841.Google Scholar
Sethuraman, J. and Sethuraman, S. (2004). On counts of Bernoulli strings and connections to rank orders and random permutations. In A festschrift for Herman Rubin (IMS Lecture Notes Monogr. Ser. 45), Institute of Mathematical Statistics, Beachwood, OH, pp. 140–152.Google Scholar