Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T17:47:05.831Z Has data issue: false hasContentIssue false
  • English
  • Français

Short-length routes in low-cost networks via Poisson line patterns

Part of: Geometric probability and stochastic geometry Operations research and management science

Published online by Cambridge University Press:  01 July 2016

David J. Aldous  and
Wilfrid S. Kendall
David J. Aldous*
Affiliation:
University of California, Berkeley
Wilfrid S. Kendall*
Affiliation:
The University of Warwick
*
∗ Postal address: Department of Statistics, 367 Evans Hall # 3860, University of California, Berkeley, CA 94720, USA. Email address: aldous@stat.berkeley.edu
∗∗ Postal address: Department of Statistics, The University of Warwick, Coventry CV4 7AL, UK. Email address: w.s.kendall@warwick.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In designing a network to link n points in a square of area n, we might be guided by the following two desiderata. First, the total network length should not be much greater than the length of the shortest network connecting all points. Second, the average route length (taken over source-destination pairs) should not be much greater than the average straight-line distance. How small can we make these two excesses? Speaking loosely, for a nondegenerate configuration, the total network length must be at least of order n and the average straight-line distance must be at least of order n1/2, so it seems implausible that a single network might exist in which the excess over the first minimum is o(n) and the excess over the second minimum is o(n1/2). But in fact we can do better: for an arbitrary configuration, we can construct a network where the first excess is o(n) and the second excess is almost as small as O(log n). The construction is conceptually simple and uses stochastic methods: over the minimum-length connected network (Steiner tree) superimpose a sparse stationary and isotropic Poisson line process. Together with a few additions (required for technical reasons), the mean values of the excess for the resulting random network satisfy the above asymptotics; hence, a standard application of the probabilistic method guarantees the existence of deterministic networks as required (speaking constructively, such networks can be constructed using simple rejection sampling). The key ingredient is a new result about the Poisson line process. Consider two points a distance r apart, and delete from the line process all lines which separate these two points. The resulting pattern of lines partitions the plane into cells; the cell containing the two points has mean boundary length approximately equal to 2r + constant(log r). Turning to lower bounds, consider a sequence of networks in 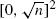satisfying a weak equidistribution assumption. We show that if the first excess is O(n) then the second excess cannot be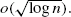

Keywords

Buffon argumentexcess statisticmark distributionspatial networkPoisson line processprobabilistic methodratio statisticSlivynak theoremSteiner treeVasershtein couplingtotal variation distance

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Secondary: 90B15: Network models, stochastic
Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 40 , Issue 1 , March 2008 , pp. 1 - 21
Copyright
Copyright © Applied Probability Trust 2008 

References

Gastner, M. T. and Newman, M. E. J. (2006). Shape and efficiency in spatial distribution networks. J. Statist. Mech. Theory Experiment 2006, P01015.CrossRefGoogle Scholar
Hug, D., Reitzner, M. and Schneider, R. (2004). The limit shape of the zero cell in a stationary Poisson hyperplane tessellation. Ann. Prob. 32, 1140–1167.CrossRefGoogle Scholar
Kovalenko, I. N. (1997). A proof of a conjecture of David Kendall on the shape of random polygons of large area. Kibernet. Sistem. Anal. 1997, 187 (in Russian). English translation: Cybernet. Systems Anal. 33, 461-467.Google Scholar
Kovalenko, I. N. (1999). A simplified proof of a conjecture of D. G. Kendall concerning shapes of random polygons. J. Appl. Math. Stoch. Anal. 12, 301–310.CrossRefGoogle Scholar
Lawler, G. F., Schramm, O. and Werner, W. (2004). Conformal invariance of planar loop-erased random walks and uniform spanning trees. Ann. Prob. 32, 939–995.CrossRefGoogle Scholar
Miles, R. E. (1995). A heuristic proof of a long-standing conjecture of D. G. Kendall concerning the shapes of certain large random polygons. Adv. Appl. Prob. 27, 397–417.CrossRefGoogle Scholar
Read, N. (2005). Minimum spanning trees and random resistor networks in d dimensions. Phys. Rev. E 72, 036114.CrossRefGoogle ScholarPubMed
Schweitzer, F., Ebeling, W., Rose, H. and Weiss, O. (1998). Optimization of road networks using evolutionary strategies. Evolutionary Comput. 5, 419–438.CrossRefGoogle Scholar
Steele, J. M. (1997). Probability Theory and Combinatorial Optimization (CBMS-NSF Regional Conf. Ser. Appl. Math. 69). Society for Industrial and Applied Mathematics, Philadelphia, PA.CrossRefGoogle Scholar
Stoyan, D., Kendall, W. S. and Mecke, J. (1995). Stochastic Geometry and Its Applications, 2nd edn. John Wiley, Chichester.Google Scholar
Yukich, J. E. (1998). Probability Theory of Classical Euclidean Optimization Problems (Lecture Notes Math. 1675). Springer, Berlin.CrossRefGoogle Scholar