Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T15:09:40.736Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral alignment of correlated Gaussian matrices

Part of: Algorithms - Computer Science Probability theory on algebraic and topological structures

Published online by Cambridge University Press:  28 January 2022

Luca Ganassali ,
Marc Lelarge  and
Laurent Massoulié
Luca Ganassali*
Affiliation:
Inria, DI/ENS, PSL Research University
Marc Lelarge*
Affiliation:
Inria, DI/ENS, PSL Research University
Laurent Massoulié*
Affiliation:
MSR–Inria Joint Center and Inria, DI/ENS, PSL Research University
*
*Postal address: Inria, 2 rue Simone Iff, 75012 Paris, France.
*Postal address: Inria, 2 rue Simone Iff, 75012 Paris, France.
*Postal address: Inria, 2 rue Simone Iff, 75012 Paris, France.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we analyze a simple spectral method (EIG1) for the problem of matrix alignment, consisting in aligning their leading eigenvectors: given two matrices A and B, we compute two corresponding leading eigenvectors $v_1$ and 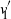$v'_{\!\!1}$ . The algorithm returns the permutation 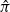$\hat{\pi}$ such that the rank of coordinate 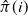$\hat{\pi}(i)$ in 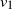$v_1$ and that of coordinate i in 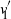$v'_{\!\!1}$ (up to the sign of 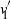$v'_{\!\!1}$ ) are the same.

We consider a model of weighted graphs where the adjacency matrix A belongs to the Gaussian orthogonal ensemble of size 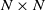$N \times N$ , and B is a noisy version of A where all nodes have been relabeled according to some planted permutation 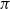$\pi$ ; that is, 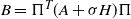$B= \Pi^T (A+\sigma H) \Pi $ , where 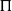$\Pi$ is the permutation matrix associated with 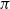$\pi$ and H is an independent copy of A. We show the following zero–one law: with high probability, under the condition 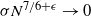$\sigma N^{7/6+\epsilon} \to 0$ for some 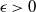$\epsilon>0$ , EIG1 recovers all but a vanishing part of the underlying permutation 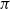$\pi$ , whereas if 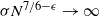$\sigma N^{7/6-\epsilon} \to \infty$ , this method cannot recover more than o(N) correct matches.

This result gives an understanding of the simplest and fastest spectral method for matrix alignment (or complete weighted graph alignment), and involves proof methods and techniques which could be of independent interest.

Keywords

Graph alignmentrandom matricesspectral theory

MSC classification

Primary: 68W40: Analysis of algorithms
Secondary: 60B20: Random matrices (probabilistic aspects; for algebraic aspects see )
Type
Original Article
Information
Advances in Applied Probability , Volume 54 , Issue 1 , March 2022 , pp. 279 - 310
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allez, R. and Bouchaud, J.-P. (2014). Eigenvector dynamics under free addition. Random Matrices Theory Appl. 3, 1450010.10.1142/S2010326314500105CrossRefGoogle Scholar
Allez, R., Bun, J. and Bouchaud, J.-P. (2014). The eigenvectors of Gaussian matrices with an external source. Preprint. Available at https://arxiv.org/abs/1412.7108.Google Scholar
Anderson, G. W., Guionnet, A. and Zeitouni, O. (2009). An Introduction to Random Matrices. Cambridge University Press.10.1017/CBO9780511801334CrossRefGoogle Scholar
Bollobás, B. (2001). Random Graphs, 2nd edn. Cambridge University Press.10.1017/CBO9780511814068CrossRefGoogle Scholar
Chatterjee, S. (2014). Superconcentration and Related Topics. Springer, Cham.10.1007/978-3-319-03886-5CrossRefGoogle Scholar
Conte, D., Foggia, P., Vento, M. and Sansone, C. (2004). Thirty years of graph matching in pattern recognition. Internat. J. Pattern Recogn. Artif. Intellig. 18, 265–298.10.1142/S0218001404003228CrossRefGoogle Scholar
Ding, J., Ma, Z., Wu, Y. and Xu, J. (2018). Efficient random graph matching via degree profiles. Preprint. Available at https://arxiv.org/abs/1811.07821.Google Scholar
Erdös, L., Yau, H.-T. and Yin, J. (2010). Rigidity of eigenvalues of generalized Wigner matrices. Preprint. Available at https://arxiv.org/abs/1007.4652.Google Scholar
Fan, Z., Mao, C., Wu, Y. and Xu, J. (2019). Spectral graph matching and regularized quadratic relaxations I: the Gaussian model. Preprint. Available at https://arxiv.org/abs/1907.08880.Google Scholar
Fan, Z., Mao, C., Wu, Y. and Xu, J. (2019). Spectral graph matching and regularized quadratic relaxations II: Erdös–Rényi graphs and universality. Preprint. Available at https://arxiv.org/abs/1907.08883.Google Scholar
Feizi, S. et al. (2017). Spectral alignment of graphs. Preprint. Available at https://arxiv.org/abs/1602.04181.Google Scholar
Forrester, P. (1993). The spectrum edge of random matrix ensembles. Nuclear Phys. B 402, 709–728.10.1016/0550-3213(93)90126-ACrossRefGoogle Scholar
Haghighi, A. D., Ng, A. Y. and Manning, C. D. (2005). Robust textual inference via graph matching. In Proc. Conference on Human Language Technology and Empirical Methods in Natural Language Processing (HLT ’05), Association for Computational Linguistics, Stroudsburg, PA, pp. 387–394.10.3115/1220575.1220624CrossRefGoogle Scholar
Makarychev, K., Manokaran, R. and Sviridenko, M. (2014). Maximum quadratic assignment problem: reduction from maximum label cover and LP-based approximation algorithm. Preprint. Available at https://arxiv.org/abs/1403.7721.10.1145/2629672CrossRefGoogle Scholar
Narayanan, A. and Shmatikov, V. (2008). Robust de-anonymization of large sparse datasets. In 2008 IEEE Symposium on Security and Privacy, Institute of Electrical and Electronics Engineers, New York, pp. 111–125.10.1109/SP.2008.33CrossRefGoogle Scholar
Narayanan, A. and Shmatikov, V. (2009). De-anonymizing social networks. In 2009 IEEE Symposium on Security and Privacy, Institute of Electrical and Electronics Engineers, New York, pp. 173–187.10.1109/SP.2009.22CrossRefGoogle Scholar
O’Rourke, S. (2010). Gaussian fluctuations of eigenvalues in Wigner random matrices. J. Statist. Phys. 138, 1045–1066.10.1007/s10955-009-9906-yCrossRefGoogle Scholar
O’Rourke, S., Vu, V. and Wang, K. (2016). Eigenvectors of random matrices: a survey. Preprint. Available at https://arxiv.org/abs/1601.03678.Google Scholar
Pardalos, P., Rendl, F. and Wolkowicz, H. (1994). The quadratic assignment problem: a survey and recent developments. In Quadratic Assignment and Related Problems, eds Pardalos, P. and Wolkowicz, H., American Mathematical Society, Providence, RI, pp. 1–42.10.1090/dimacs/016/01CrossRefGoogle Scholar
Singh, R., Xu, J. and Berger, B. (2008). Global alignment of multiple protein interaction networks with application to functional orthology detection. Proc. Nat. Acad. Sci. USA 105, 12763–12768.10.1073/pnas.0806627105CrossRefGoogle Scholar
Tracy, C. A. and Widom, H. (1998). Correlation functions, cluster functions, and spacing distributions for random matrices. J. Statist. Phys. 92, 809–835.10.1023/A:1023084324803CrossRefGoogle Scholar