Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T11:28:22.805Z Has data issue: false hasContentIssue false
  • English
  • Français

State space expansions and the limiting behavior of quasi-birth-and-death processes

Published online by Cambridge University Press:  01 July 2016

Steven L. Beuerman  and
Edward J. Coyle
Get access Rights & Permissions [Opens in a new window]

Abstract

The notion of complete level crossing information, or LCI-completeness, is introduced for quasi-birth-death (QBD) processes. It is shown that state space expansions allow any QBD-process to be modified so that it is LCI-complete.

For any LCI-complete, QBD-process, there exists a matrix W such that 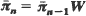, where 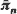is the vector of limiting probabilities for all states on level n of the process. When W cannot be found in closed form, it can be found via an algorithm requiring fewer than m steps, where m is the number of states on each level of the process. The result of this algorithm is always a linear matrix equation for which W is the solution.

In essentially all cases considered in this paper, the matrix W is a solution of the matrix quadratic

X2A2 + XA1 + A0 = 0.

Despite this fact, W is never equal to Neuts' rate matrix R, although the non-zero eigenvalues and the corresponding left eigenvectors of R are a subset of the eigenvalues and left eigenvectors of W. This fact leads to two methods for determining R from W.

If the transition rates of the QBD-process are level-dependent, then it is also shown that matrices W(n) exist such that .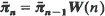

Keywords

RATE MATRIXMATRIX-GEOMETRIC SOLUTIONCOMPLETE LEVEL CROSSING INFORMATIONLCI-COMPLETENESS
Type
Research Article
Information
Advances in Applied Probability , Volume 21 , Issue 2 , June 1989 , pp. 284 - 314
Copyright
Copyright © Applied Probability Trust 1989 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was supported by a grant from AT&T, by Purdue's Engineering Research Center for Intelligent Manufacturing Systems, and by a David Ross Fellowship.

References

[1] Beuerman, S. L. and Coyle, E. J. (1986) Quasi-birth-death processes and their use in the modelling and analysis of computer networks. TR-EE 86–20, Dept. of Electrical Engineering, Purdue University.Google Scholar
[2] Coyle, E. J. and Liu, B. (1983) A matrix representation of CSMA/CD networks. ICC '83, Boston, MA, 745–748.Google Scholar
[3] Coyle, E. J. and Liu, B. (1985) A matrix representation of CSMA/CD networks. IEEE Trans. Comm. 33, 53–64.Google Scholar
[4] Evans, R. V. (1967) Geometric distribution in some two-dimensional queueing systems. Operat. Res. 15, 830–846.Google Scholar
[5] Neuts, M. F. (1981) Matrix-Geometric Solutions in Stochastic Models. Johns Hopkins University Press, Baltimore, MD.Google Scholar
[6] Wallace, V. (1969) The Solution of Quasi Birth and Death Processes Arising from Multiple Access Computer Systems. Ph.D. Dissertation, Systems Engineering Laboratory, University of Michigan.Google Scholar
[7] Zhang, J. and Coyle, E. J. (1988) Matrix recursive solutions in quasi-birth-death models of random access networks. IEEE Internat. Symp. Information Theory, Kobe, Japan.Google Scholar
[8] Zhang, J. and Coyle, E. J. (1988) Matrix recursive solutions for the transient behaviour of quasi-birth-death processes and its application to random access networks. 22nd Conference on Information Science and Systems, Princeton University, Princeton, NJ.Google Scholar