Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T11:12:18.235Z Has data issue: false hasContentIssue false
  • English
  • Français

Statistical inference for Markov processes when the model is incorrect

Published online by Cambridge University Press:  01 July 2016

Robert V. Foutz  and
R. C. Srivastava
Robert V. Foutz*
Affiliation:
Virginia Polytechnic Institute and State University
R. C. Srivastava*
Affiliation:
The Ohio State University
*
∗Postal address: Department of Statistics and Statistical Laboratory, Virginia Polytechnic Institute and State University, Blacksburg VA24061, U.S.A.
∗∗Postal address: Department of Statistics, The Ohio State University, Cockins Hall, 1958 Neil Avenue, OH 43210, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

Statistical inference for Markov processes is commonly based on the maximum likelihood method of estimation and the likelihood ratio criterion for testing hypotheses. Construction of estimators and test statistics by these methods require that a model be chosen in the form of a family of transition density functions. In this paper, asymptotic properties of the maximum likelihood estimator 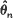and of the likelihood ratio statistic λn are examined when the model chosen for their construction is incorrect—that is, when no density in the model is a density for the transition probability distribution of the Markov process. It is shown that if 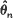and λn are constructed from a ‘regular’ incorrect model, then 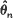is consistent and asymptotically normally distributed and the asymptotic null distribution of −2 log λn is that of a linear combination of independent chi-squared random variables. These results are applied to propose measures of the performance of the test based on λn when the statistic is constructed from an incorrect model.

Keywords

MARKOV PROCESSESINCORRECT MODELMAXIMUM LIKELIHOOD ESTIMATORLIKELIHOOD RATIO TESTBAHADUR EFFICIENCY
Type
Research Article
Information
Advances in Applied Probability , Volume 11 , Issue 4 , December 1979 , pp. 737 - 749
Copyright
Copyright © Applied Probability Trust 1979 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bahadur, R. R. (1960) Stochastic comparison of tests. Ann. Math. Statist. 31, 276–295.Google Scholar
Bahadur, R. R. (1967) Rates of convergence of estimates and test statistics. Ann. Math. Statist. 38, 303–324.CrossRefGoogle Scholar
Billingsley, P. (1961) Statistical Inference for Markov Processes. The University of Chicago Press, Chicago.Google Scholar
Cramér, H. and Leadbetter, M. R. (1967) Stationary and Related Stochastic Processes. Wiley, New York.Google Scholar
Cramér, H. and Wold, H. (1936) Some theorems on distribution functions. J. London Math. Soc. 11, 290–295.Google Scholar
Doob, J. L. (1953) Stochastic Processes. Wiley, New York.Google Scholar
Foutz, R. V. (1977) On the unique consistent solution to the likelihood equations. J. Amer. Statist. Assoc. 72, 147–148.CrossRefGoogle Scholar
Foutz, R. V. and Srivastava, R. C. (1977) The performance of the likelihood ratio test when the model is incorrect. Ann. Statist. 5, 1183–1194.Google Scholar
Foutz, R. V. and Srivastava, R. C. (1978) The asymptotic distribution of the likelihood ratio when the model is incorrect.Google Scholar
Kullback, S. (1959) Information Theory and Statistics. Wiley, New York.Google Scholar
Wald, A. (1949) Note on the consistency of the maximum likelihood estimate. Ann. Math. Statist. 20, 595–601.CrossRefGoogle Scholar