Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T16:02:25.425Z Has data issue: false hasContentIssue false
  • English
  • Français

Subexponential potential asymptotics with applications

Part of: Special processes Mathematical economics

Published online by Cambridge University Press:  13 June 2022

Victoria Knopova  and
Zbigniew Palmowski Open the ORCID record for Zbigniew Palmowski [Opens in a new window]
Victoria Knopova*
Affiliation:
Kyiv National Taras Shevchenko University
Zbigniew Palmowski*
Affiliation:
Wrocław University of Science and Technology
*
*Postal address: Kyiv National Taras Shevchenko University, 4E Glushkov Ave, 03127, Kyiv, Ukraine. Email address: vicknopova@gmail.com
**Postal address: Faculty of Pure and Applied Mathematics, Wrocław University of Science and Technology, Wyb. Wyspiańskiego 27, 50-370 Wrocław, Poland. Email address: zbigniew.palmowski@pwr.edu.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 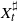$X_t^\sharp$ be a multivariate process of the form 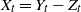$X_t =Y_t - Z_t$ 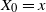, $X_0=x$ , killed at some terminal time T, where 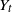$Y_t$ is a Markov process having only jumps of length smaller than 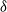$\delta$ , and 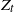$Z_t$ is a compound Poisson process with jumps of length bigger than 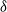$\delta$ , for some fixed 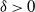$\delta>0$ . Under the assumptions that the summands in 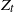$Z_t$ are subexponential, we investigate the asymptotic behaviour of the potential function 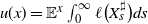$u(x)= \mathbb{E}^x \int_0^\infty \ell\big(X_s^\sharp\big)ds$ . The case of heavy-tailed entries in 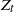$Z_t$ corresponds to the case of ‘big claims’ in insurance models and is of practical interest. The main approach is based on the fact that u(x) satisfies a certain renewal equation.

Keywords

Potentialrenewal equationsubexponential distributionapplicationsLévy processes

MSC classification

Primary: 60K20: Applications of Markov renewal processes (reliability, queueing networks, etc.)
Secondary: 60K05: Renewal theory 91B30: Risk theory, insurance
Type
Original Article
Information
Advances in Applied Probability , Volume 54 , Issue 3 , September 2022 , pp. 783 - 807
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asmussen, S. (2003). Applied Probability and Queues, 2nd edn. Springer, New York.Google Scholar
Asmussen, S. and Albrecher, H. (2010). Ruin Probabilities. World Scientific, Singapore.10.1142/7431CrossRefGoogle Scholar
Basrak, B., Davis, R. A. and Mikosch, T. (2002). A characterization of multivariate regular variation. Ann. Appl. Prob. 12, 908–920.10.1214/aoap/1031863174CrossRefGoogle Scholar
Bass, R. F. (2011). Stochastic Processes. Cambridge University Press.10.1017/CBO9780511997044CrossRefGoogle Scholar
Cadenillas, A. (2000). Consumption–investment problems with transaction costs: survey and open problems. Math. Meth. Operat. Res. 51, 43–68.10.1007/s001860050002CrossRefGoogle Scholar
Carlsson, H. and Wainger, S. (1982). An asymptotic series expansion of the multidimensional renewal measure. Compositio Math. 47, 355–364.Google Scholar
Carlsson, H. and Wainger, S. (1984). On the multidimensional renewal theorem. J. Math. Anal. Appl. 100, 316–322.10.1016/0022-247X(84)90083-0CrossRefGoogle Scholar
Chover, J., Ney, P. and Wainger, S. (1973). Degeneracy properties of subcritical branching processes. Ann. Prob. 1, 663–673.10.1214/aop/1176996893CrossRefGoogle Scholar
Chover, J., Ney, P. and Wainger, S. (1973). Functions of probability measures. J. Anal. Math. 26, 255–302.10.1007/BF02790433CrossRefGoogle Scholar
Chung, K. L. (1952). On the renewal theorem in higher dimensions. Skand. Aktuarietidskr. 35, 188–194.Google Scholar
Chung, K. L. (1982). Lectures from Markov Processes to Brownian Motion. Springer, Berlin.10.1007/978-1-4757-1776-1CrossRefGoogle Scholar
Çinlar, E. (1969). Markov renewal theory. Adv. Appl. Prob. 1, 123–187.10.2307/1426216CrossRefGoogle Scholar
Cline, D. H. (1986). Convolution tails, product tails and domains of attraction. Prob. Theory Relat. Fields 72, 529–557.10.1007/BF00344720CrossRefGoogle Scholar
Cline, D. H. (1987). Convolutions of distributions with exponential and subexponential tails. J. Austral. Math. Soc. A. 43, 347–365.10.1017/S1446788700029633CrossRefGoogle Scholar
Cline, D. H. and Resnick, S. I. (1992). Multivariate subexponential distributions. Stoch. Process. Appl. 42, 49–72.10.1016/0304-4149(92)90026-MCrossRefGoogle Scholar
Doney, R. (1966). An analogue of the renewal theorem in higher dimensions. Proc. London Math. Soc. s3-16, 669–684.10.1112/plms/s3-16.1.669CrossRefGoogle Scholar
Embrechts, P., Goldie, C. M. and Veraverbeke, N. (1979). Subexponentiality and infinite divisibility. Z. Wahrscheinlichkeitsth. 49, 335–347.10.1007/BF00535504CrossRefGoogle Scholar
Embrechts, P., Klüppelberg, C. and Mikosch, T. (1997). Modelling Extremal Events for Insurance and Finance. Springer, Berlin.10.1007/978-3-642-33483-2CrossRefGoogle Scholar
Embrechts, P. and Goldie, C. M. (1980). On closure and factorization properties of subexponential and related distributions. J. Austral. Math. Soc. A 29, 243–256.10.1017/S1446788700021224CrossRefGoogle Scholar
Embrechts, P. and Goldie, C. M. (1982). On convolution tails. Stoch. Process. Appl. 13, 263–278.10.1016/0304-4149(82)90013-8CrossRefGoogle Scholar
Feller, W. (1971). An Introduction to Probability Theory and Its Applications, Vol. II, 2nd edn. John Wiley, New York.Google Scholar
Feng, R. and Shimizu, Y. (2014). Potential measure of spectrally negative Markov additive process with applications in ruin theory. Insurance Math. Econom. 59, 11–26.10.1016/j.insmatheco.2014.08.001CrossRefGoogle Scholar
Foss, S., Korshunov, D. and Zachary, S. (2013). An Introduction to Heavy-Tailed and Subexponential Distributions, 2nd edn. Springer, New York.10.1007/978-1-4614-7101-1CrossRefGoogle Scholar
Foss, S., Korshunov, D., Palmowski, Z. and Rolski, T. (2017). Two-dimensional ruin probability for subexponential claim size. Prob. Math. Statist. 37, 319–335.Google Scholar
Höglund, T. (1988). A multidimensional renewal theorem. Bull. Sci. Math. 112, 111–138.Google Scholar
Knopova, V. (2011). Asymptotic behaviour of the distribution density of some Lévy functionals in $\mathbb{R}^n$ . Theory Stoch. Process. 17, 35–54.Google Scholar
Knopova, V. and Kulik, A. (2011). Exact asymptotic for distribution densities of Lévy functionals. Electron. J. Prob. 16, 1394–1433.10.1214/EJP.v16-909CrossRefGoogle Scholar
Knopova, V. and Schilling, R. (2012). Transition density estimates for a class of Lévy and Lévy-type processes. J. Theoret. Prob. 25, 144–170.CrossRefGoogle Scholar
Kyprianou, A. (2013). Gerber–Shiu Risk Theory. Springer, Cham.Google Scholar
Merton, R. C. (1969). Lifetime portfolio selection under uncertainty: the continuous-time case. Rev. Econom. Statist. 51, 247–257.10.2307/1926560CrossRefGoogle Scholar
Mikosch, T. (1997). Heavy-tailed modelling in insurance. Commun. Statist. Stoch. Models 13, 799–815.10.1080/15326349708807452CrossRefGoogle Scholar
Nagaev, A. V. (1979). Renewal theorems in ${\unicode{x211D}^d}$ . Teor. Veroyat. Primen. 24, 565–573.Google Scholar
Omey, E. (2006). Subexponential distribution functions in ${\unicode{x211D}^d}$ . J. Math. Sci. 138, 5434–5449.10.1007/s10958-006-0310-8CrossRefGoogle Scholar
Omey, E., Mallor, F. and Santos, J. (2006). Multivariate subexponential distributions and random sums of random vectors. Adv. Appl. Prob. 38, 1028–1046.CrossRefGoogle Scholar
Resnick, S. (2008). Multivariate regular variation on cones: application to extreme values, hidden regular variation and conditioned limit laws. (English summary.) Stochastics 80, 269–298.CrossRefGoogle Scholar
Rolski, T., Schmidli, H., Schmidt, H. and Teugels, J. (2009). Stochastic Processes for Insurance and Finance. John Wiley, New York.Google Scholar
Schilling, R. (2017). Measures, Integrals and Martingales, 2nd edn. Cambridge University Press.Google Scholar
Sharpe, M. (1988). General Theory of Markov Processes. Academic Press, London.Google Scholar
Stone, C. (1965). On characteristic functions and renewal theory. Trans. Amer. Math. Soc. 120, 327–342.CrossRefGoogle Scholar
Willmot, G. E., Cai, J. and Lin, X. S. (2001). Lundberg inequalities for renewal equations. Adv. Appl. Prob. 33, 674–689.CrossRefGoogle Scholar
Yin, C. and Zhao, J. (2006). Nonexponential asymptotic for the solutions of renewal equations, with applications. J. Appl. Prob. 43, 815–824.10.1239/jap/1158784948CrossRefGoogle Scholar