Hostname: page-component-7dd5485656-g8tfn Total loading time: 0 Render date: 2025-10-29T12:23:41.183Z Has data issue: false hasContentIssue false
  • English
  • Français

The surface pair correlation function for stationary Boolean models

Part of: Stochastic processes Geometric probability and stochastic geometry

Published online by Cambridge University Press:  01 July 2016

Felix Ballani
Felix Ballani*
Affiliation:
Freie Universität Berlin
*
∗ Postal address: AG Mathematical Geometry Processing, Freie Universität Berlin, Arnimallee 3, D-14195 Berlin, Germany. Email address: ballani@mi.fu-berlin.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

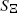The random surface measure of a stationary Boolean model 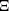with grains from the convex ring is considered. A sufficient condition and a necessary condition for the existence of the density of the second-order moment measure of 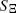are given and a representation of this density is derived. As applications, the surface pair correlation functions of a Boolean model with spheres and a Boolean model with randomly oriented right circular cylinders in ℝ3 are determined.

Keywords

Random setBoolean modelsurface measuresecond-order moment measureproduct densitypair correlation function

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry 60G57: Random measures

Information

Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 39 , Issue 1 , March 2007 , pp. 1 - 15
Copyright
Copyright © Applied Probability Trust 2007 

References

Arns, C. H., Mecke, J., Mecke, K. R. and Stoyan, D. (2005). Second-order analysis by variograms for curvature measures of two-phase structures. Europ. Phys. J. B 47, 397–409.CrossRefGoogle Scholar
Ballani, F. (2006). Beiträge zur Theorie und Anwendung von Keim-Korn-Modellen mit konvexen Körnern. , Technische Universität Bergakademie Freiberg.Google Scholar
Böhm, S. and Schmidt, V. (2003). Palm representation and approximation of the covariance of random closed sets. Adv. Appl. Prob. 35, 295–302.CrossRefGoogle Scholar
Daley, D. J. and Vere-Jones, D. (2003). An Introduction to the Theory of Point Processes, Vol. I, Elementary Theory and Methods, 2nd edn. Springer, New York.Google Scholar
Doi, M. (1976). A new variational approach to the diffusion and the flow problems in porous media. J. Phys. Soc. Japan 40, 567–572.CrossRefGoogle Scholar
Gille, W. (1987). The chord length distribution of the right circular cylinder. Exp. Tech. Phys. 35, 93–98.Google Scholar
Heinrich, L. and Molchanov, I. S. (1999). Central limit theorem for a class of random measures associated with germ-grain models. Adv. Appl. Prob. 31, 283–314.CrossRefGoogle Scholar
Hug, D. and Last, G. (2000). On support measures in Minkowski spaces and contact distributions in stochastic geometry. Ann. Prob. 28, 796–850.CrossRefGoogle Scholar
Mecke, J. (1967). Stationäre zufällige Masse auf lokalkompakten Abelschen Gruppen. Z. Wahrscheinlichkeitsth. 9, 36–58.CrossRefGoogle Scholar
Mecke, K. R. (2001). Exact moments of curvature measures in the Boolean model. J. Statist. Phys. 102, 1343–1381.CrossRefGoogle Scholar
Molchanov, I. S. (1995). Statistics of the Boolean model: from the estimation of means to the estimation of distributions. Adv. Appl. Prob. 27, 63–86.CrossRefGoogle Scholar
Schneider, R. (1993). Convex Bodies: the Brunn–Minkowski Theory. Cambridge University Press.CrossRefGoogle Scholar
Schneider, R. and Weil, W. (2000). Stochastische Geometrie. Teubner, Stuttgart.CrossRefGoogle Scholar
Stoyan, D. and Stoyan, H. (1994). Fractals, Random Shapes and Point Fields. John Wiley, Chichester.Google Scholar
Stoyan, D., Kendall, W. S. and Mecke, J. (1995). Stochastic Geometry and Its Applications. John Wiley, Chichester.Google Scholar
Stoyan, D., Mecke, J. and Pohlmann, S. (1980). Formulas for stationary planar fibre processes. II. Partially oriented fibre systems. Math. Operat. Statist. Ser. Statist. 11, 281–286.Google Scholar
Torquato, S. (1986). Interfacial surface statistics arising in diffusion and flow problems in porous media. J. Chem. Phys. 85, 4622–4628.CrossRefGoogle Scholar
Torquato, S. (2002). Random Heterogeneous Materials. Microstructure and Macroscopic Properties. Springer, New York.CrossRefGoogle Scholar