Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T10:40:09.734Z Has data issue: false hasContentIssue false
  • English
  • Français

Yaglom limit for stochastic fluid models

Part of: Discrete mathematics in relation to computer science Theory of computing

Published online by Cambridge University Press:  08 October 2021

Nigel G. Bean ,
Małgorzata M. O’Reilly Open the ORCID record for Małgorzata M. O’Reilly [Opens in a new window]  and
Zbigniew Palmowski Open the ORCID record for Zbigniew Palmowski [Opens in a new window]
Nigel G. Bean*
Affiliation:
University of Adelaide
Małgorzata M. O’Reilly*
Affiliation:
University of Tasmania
Zbigniew Palmowski*
Affiliation:
Wrocław University of Science and Technology
*
*Postal address: Australian Research Council Centre of Excellence for Mathematical and Statistical Frontiers. School of Mathematical Sciences, University of Adelaide, SA 5005 Australia. Email: nigel.bean@adelaide.edu.au
**Postal address: Australian Research Council Centre of Excellence for Mathematical and Statistical Frontiers. Discipline of Mathematics, University of Tasmania, Hobart TAS 7001, Australia. Email: malgorzata.oreilly@utas.edu.au
***Postal address: Faculty of Pure and Applied Mathematics, Wrocław University of Science and Technology, ul. Wybrzeże Wyspiańskiego 27, 50-370 Wrocław, Poland. Email: zbigniew.palmowski@pwr.edu.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we analyse the limiting conditional distribution (Yaglom limit) for stochastic fluid models (SFMs), a key class of models in the theory of matrix-analytic methods. So far, only transient and stationary analyses of SFMs have been considered in the literature. The limiting conditional distribution gives useful insights into what happens when the process has been evolving for a long time, given that its busy period has not ended yet. We derive expressions for the Yaglom limit in terms of the singularity˜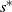$s^*$ such that the key matrix of the SFM, 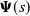${\boldsymbol{\Psi}}(s)$, is finite (exists) for all 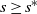$s\geq s^*$ and infinite for 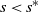$s<s^*$. We show the uniqueness of the Yaglom limit and illustrate the application of the theory with simple examples.

Keywords

Stochastic fluid modelMarkov chainLaplace–Stieltjes transformYaglom limitlimiting conditional distribution

MSC classification

Primary: 68Q25: Analysis of algorithms and problem complexity 68R10: Graph theory (including graph drawing)
Secondary: 68U05: Computer graphics; computational geometry
Type
Original Article
Information
Advances in Applied Probability , Volume 53 , Issue 3 , September 2021 , pp. 649 - 686
Check for updates
Copyright
© The Author(s) 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abate, J. and Whitt, W. (1997). Asymptotics for M/G/1 low-priority waiting-time tail probabilities. Queueing Systems 25, 173–233.CrossRefGoogle Scholar
Ahn, S. and Ramaswami, V. (2003). Fluid flow models and queues—a connection by stochastic coupling. Stoch. Models 19, 325–348.CrossRefGoogle Scholar
Ahn, S. and Ramaswami, V. (2004). Transient analysis of fluid flow models via stochastic coupling to a queue. Stoch. Models 20, 71–101.CrossRefGoogle Scholar
Ahn, S. and Ramaswami, V. (2005). Efficient algorithms for transient analysis of stochastic fluid flow models. J. Appl. Prob. 42, 531–549.CrossRefGoogle Scholar
Ahn, S. and Ramaswami, V. (2006). Transient analysis of fluid models via elementary level-crossing arguments. Stoch. Models 22, 129–147.10.1080/15326340500481788CrossRefGoogle Scholar
Anick, D., Mitra, D. and Sondhi, M. (1982). Stochastic theory of a data handling system with multiple sources. Bell System Tech. J. 61, 1871–1894.CrossRefGoogle Scholar
Asmussen, S. (1995). Stationary distributions for fluid flow models with or without Brownian noise. Stoch. Models 11, 21–49.CrossRefGoogle Scholar
Asmussen, S. (2003). Applied Probability and Queues. Springer, New York.Google Scholar
Asselah, A., Ferrari, P. A., Groisman, P. and Jonckheere, M. (2016). Fleming–Viot selects the minimal quasi-stationary distribution: the Galton–Watson case. Ann. Inst. H. Poincaré Prob. Statist. 52, 647–668.CrossRefGoogle Scholar
Bean, N. et al. (1997). The quasi-stationary behavior of quasi-birth-and-death processes. Ann. Appl. Prob. 7, 134–155.CrossRefGoogle Scholar
Bean, N., Pollett, P. and Taylor, P. (1998). Quasistationary distributions for level-independent quasi-birth-and-death processes. Commun. Statist. Stoch. Models 14, 389–406.CrossRefGoogle Scholar
Bean, N., Pollett, P. and Taylor, P. (2000). Quasistationary distributions for level-dependent quasi-birth-and-death processes. Commun. Statist. Stoch. Models 16, 511–541.CrossRefGoogle Scholar
Bean, N. G. and O’Reilly, M. M. (2013). Spatially-coherent uniformization of a stochastic fluid model to a quasi-birth-and-death process. Performance Evaluation 70, 578–592.CrossRefGoogle Scholar
Bean, N. G. and O’Reilly, M. M. (2014). The stochastic fluid–fluid model: a stochastic fluid model driven by an uncountable-state process, which is a stochastic fluid model itself. Stoch. Process. Appl. 124, 1741–1772.10.1016/j.spa.2013.12.006CrossRefGoogle Scholar
Bean, N. G., O’Reilly, M. M. and Taylor, P. G. (2005). Algorithms for return probabilities for stochastic fluid flows. Stoch. Models 21, 149–184.10.1081/STM-200046511CrossRefGoogle Scholar
Bean, N. G., O’Reilly, M. M. and Taylor, P. G. (2005). Hitting probabilities and hitting times for stochastic fluid flows. Stoch. Process. Appl. 115, 1530–1556.10.1016/j.spa.2005.04.002CrossRefGoogle Scholar
Bean, N. G., O’Reilly, M. M. and Taylor, P. G. (2008). Algorithms for the Laplace–Stieltjes transforms of first return times for stochastic fluid flows. Methodology Comput. Appl. Prob. 10, 381–408.CrossRefGoogle Scholar
Bhatia, R. and Rosenthal, P. (1997). How and why to solve the operator equation $AX-XB=Y$. Bull. London Math. Soc. 29, 1–21.CrossRefGoogle Scholar
Bogdan, K., Palmowski, Z. and Wang, L. (2018). Yaglom limit for stable processes in cones. Electron. J. Prob. 23, 1–19.CrossRefGoogle Scholar
Collet, P., Martnez, S. and San Martn, J. (2013). Quasi-Stationary Distributions. Springer, Berlin, Heidelberg.CrossRefGoogle Scholar
Darroch, J. and Seneta, E. (1965). On quasi-stationary distributions in absorbing discrete-time Markov chains. J. Appl. Prob. 2, 88–100.CrossRefGoogle Scholar
Doetsch, G. (1974). Introduction to the Theory and Application of the Laplace Transformation. Springer, Berlin.10.1007/978-3-642-65690-3CrossRefGoogle Scholar
Ferrari, P. A., Kesten, H., Martínez, S. and Picco, P. (1995). Existence of quasi-stationary distributions. A renewal dynamical approach. Ann. Prob. 23, 501–521.CrossRefGoogle Scholar
Ferrari, P. A. and Marić, N. (2007). Quasi stationary distributions and Fleming–Viot processes in countable spaces. Electron. J. Prob. 12, 684–702.10.1214/EJP.v12-415CrossRefGoogle Scholar
Flaspohler, D. C. and Holmes, P. T. (1972). Additional quasi-stationary distributions for semi-Markov processes. J. Appl. Prob. 9, 671–676.CrossRefGoogle Scholar
Foley, R. and McDonald, D. (2017). Yaglom limits can depend on the starting state. Preprint. Available at https://arxiv.org/abs/1709.07578.Google Scholar
Guo, C. (2002). Nonsymmetric algebraic Riccati equations and Wiener–Hopf factorization for M-matrices. SIAM J. Matrix Anal. Appl. 23, 225–242.CrossRefGoogle Scholar
Haas, B. and Rivero, V. (2012). Quasi-stationary distributions and Yaglom limits of self-similar Markov processes. Stoch. Process. Appl. 122, 4054–4095.CrossRefGoogle Scholar
He, Q. (2013). Fundamentals of Matrix-Analytic Methods. Springer, New York.Google Scholar
Henrici, P. (1977). Applied and Computational Complex Analysis, Vol. 2. John Wiley, New York.Google Scholar
Iglehart, D. L. (1974). Random walks with negative drift conditioned to stay positive. J. Appl. Prob. 11, 742–751.CrossRefGoogle Scholar
Jacka, S. D. and Roberts, G. O. (1995). Weak convergence of conditioned processes on a countable state space. J. Appl. Prob. 32, 902–916.CrossRefGoogle Scholar
Kyprianou, A. E. and Palmowski, Z. (2006). Quasi-stationary distributions for Lévy processes. Bernoulli 12, 571–581.CrossRefGoogle Scholar
Kyprianou, E. K. (1971). On the quasi-stationary distribution of the virtual waiting time in queues with Poisson arrivals. J. Appl. Prob. 8, 494–507.CrossRefGoogle Scholar
Lambert, A. (2007). Quasi-stationary distributions and the continuous-state branching process conditioned to be never extinct. Electron. J. Prob. 12, 420–446.CrossRefGoogle Scholar
Latouche, G. and Ramaswami, V. (1999). Introduction to Matrix Analytic Methods in Stochastic Modeling. Society for Industrial and Applied Mathematics, Philadelphia.CrossRefGoogle Scholar
Latouche, G. et al. (2013). Matrix-Analytic Methods in Stochastic Models. Springer, New York.CrossRefGoogle Scholar
Laub, A. (2005). Matrix Analysis for Scientists and Engineers. Society for Industrial and Applied Mathematics, Philadelphia.CrossRefGoogle Scholar
Mandjes, M., Palmowski, Z. and Rolski, T. (2012). Quasi-stationary workload in a Lévy-driven storage system. Stoch. Models 28, 413–432.CrossRefGoogle Scholar
Martnez, S. and San Martn, J. (1994). Quasi-stationary distributions for a Brownian motion with drift and associated limit laws. J. Appl. Prob. 31, 911–920.CrossRefGoogle Scholar
Miyazawa, M. and Rolski, T. (2009). Exact asymptotics for a Lévy-driven tandem queue with an intermediate input. Queueing Systems 63, 323–353.CrossRefGoogle Scholar
Pollett, P. (2015). Quasi-stationary distributions: a bibliography. Available at www.maths.uq.edu.au/pkp/papers/qsds/qsds.pdf.Google Scholar
Ramaswami, V. (1996). Matrix analytic methods: a tutorial overview with some extensions and new results. In Matrix-Analytic Methods in Stochastic Models (Lecture Notes Pure Appl. Math. 183), Dekker, New York, pp. 261–296.CrossRefGoogle Scholar
Ramaswami, V. (1999). Matrix analytic methods for stochastic fluid flows. In Teletraffic Engineering in a Competitive World—Proc. 16th International Teletraffic Congress, Elsevier, Amsterdam, pp. 1019–1030.Google Scholar
Seneta, E. and Vere-Jones, D. (1966). On quasi-stationary distributions in discrete-time Markov chains with a denumerable infinity of states. J. Appl. Prob. 3, 403–434.CrossRefGoogle Scholar
Tweedie, R. L. (1974). Quasi-stationary distributions for Markov chains on a general state space. J. Appl. Prob. 11, 726–741.CrossRefGoogle Scholar
Van Doorn, E. A. (1991). Quasi-stationary distributions and convergence to quasi-stationarity of birth–death processes. Adv. Appl. Prob. 23, 683–700.CrossRefGoogle Scholar
Yaglom, A. M. (1947). Certain limit theorems of the theory of branching random processes. Dokl. Akad. Nauk. SSSR (N.S.) 56, 795–798.Google Scholar
Zhang, J., Li, S. and Song, R. (2014). Quasi-stationarity and quasi-ergodicity of general Markov processes. Sci. China Math. 57, 2013–2024.CrossRefGoogle Scholar