Article contents
Profile Fitting by the Interference Function
Published online by Cambridge University Press: 06 March 2019
Abstract
On the basis of the “column-like” powder model of Warren and Averbach, a profile fitting procedure was devised to obtain microstructural disorder parameters. The interference function
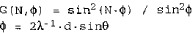
where d is the interplanar distance, λ the wavelength, θ the diffraction angle and N the number of cells within a column, was used to model experimental profiles taking into account the column-like crystallite size and r.m.s. strain distributions. The procedure can be applied both to single peak and to two or more peaks of multiple order of reflection. The method was tested on several samples, also having a bimodal size distribution, and the results compared with those obtained by the well-established Warren-Averbach analysis.
Information
- Type
- VIII. XRD Profile Fitting, Crystallite Size and Strain Determination
- Information
- Copyright
- Copyright © International Centre for Diffraction Data 1991
References
- 1
- Cited by

