Article contents
Quantitative flow diagnostics of shock trains by rainbow schlieren deflectometry
Published online by Cambridge University Press: 18 July 2022
Abstract
A new measurement technique to reconstruct the density field of the shock-wave/boundary-layer interaction (SWBLI) in a confined duct is proposed. With this technique, it is possible to quantitatively capture in detail the structures of the density field both in the regions of the shock-systems in the central core and boundary-layer flows near the duct wall concurrently. The novel feature of the proposed technique is to make use of the schlieren images with the rainbow filters of the vertical and horizontal cutoff settings and then to reconstruct the two-dimensional density field integrated over the line-of-sight direction using the corresponding filter calibration curves. The proposed technique is applied for the first time to a shock train in a constant-area straight duct under the upstream condition of the shock train: the freestream Mach number is 1.42, the incoming boundary layer thickness normalised by the duct half height is 0.175, and the corresponding unit Reynolds number 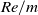 $Re/m$ is
$Re/m$ is 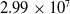 $2.99 \times 10^7$ m-1. The calculated isopycnic field depicts the streamwise and transverse density variations inside the shock train, the mixing region after the shock train, and the boundary-layer of the interaction region. This technique is shown to be capable of identifying the locations of shocks in a shock train more precisely than a conventional approach measuring the static pressure distribution along the duct wall. In addition, various quantitative visual representations such as a shadowgraphy and a bright-field schlieren can be extracted from the density field acquired by the present approach, and the spatial evolution of the shape and strength of each shock constituting the shock train as well as the boundary layer flow properties can be quantitatively clarified.
$2.99 \times 10^7$ m-1. The calculated isopycnic field depicts the streamwise and transverse density variations inside the shock train, the mixing region after the shock train, and the boundary-layer of the interaction region. This technique is shown to be capable of identifying the locations of shocks in a shock train more precisely than a conventional approach measuring the static pressure distribution along the duct wall. In addition, various quantitative visual representations such as a shadowgraphy and a bright-field schlieren can be extracted from the density field acquired by the present approach, and the spatial evolution of the shape and strength of each shock constituting the shock train as well as the boundary layer flow properties can be quantitatively clarified.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Royal Aeronautical Society
References
- 1
- Cited by


