No CrossRef data available.
Article contents
Extract
In the present paper it is demonstrated that variations in the Reynolds number as due to altitude are unimportant, provided that NR at sea level is in the region of 107.
That under these conditions the law of velocity in relation to altitude, is implicitly contained in the expression W= K L ρV 2 x area, in which ρ and V only are variables; i.e., the velocity of flight must vary in the inverse ratio of 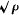 .
.
That the velocity limit due to the elasticity of air is lower at high altitude, for the velocity of sound is lower, the optimum flight velocity is higher. The facts concerning this are set forth.
- Type
- Research Article
- Information
- Copyright
- Copyright © Royal Aeronautical Society 1937
Footnotes
Part II relating to the power plant will be published in the June issue of the Journal.
References
1 C.f. Journal Aeronautical Society, February, 1937, p. 114, lines 9 et seq; and p. 124, lines 23 et seq.
2 The resistance of the ancillary organs—the tail plane, elevator, rudder, etc.—present a ”wetted” surface commonly equal to about 25 per cent, that of the aerofoil; this must be taken into account as variable, i.e., as giving rise to part of the aerofoil direct resistance. An addition of 25 per cent, to the value of Co is all that is necessary.
3 As in the author's paper “The Part Played by Skin-Friction in Aeronautics” (Journal, February, 1937), Part IV, the high Reynolds number is assumed.
4 The aeroplane here is taken as a thing “in being” and assumed not to undergo any change.
5 Loc. cit. ante.
6 Based on the “International Standard” atmosphere. In Fig. 1A the plottings are in ft./lbs./sec. units and Fig.1B in terms of c.g.s. In both temperature is expressed in degrees C.
7 See Appendix II.
8 The NR graph is sensibly straight, although there is no obvious reason why this should be so. Both NR and Co being dimensionless constants have the same value in Fig. 1A as in Fig. 1B.
9 Taken from the graph given in Fig. 2 of the author's recent paper.
10 C.f. “The Part Played by Skin-Friction in Aeronautics,” Appendix II, Fig. 23.
11 To the optimum condition.
12 The form of equation R = KρV2a applies.
13 It is nevertheless subject to a reduction on account of the fact that part only of the resistance is due to skin-friction.
14 An allowance may be made if wished.
15 This is generally speaking assumed.
16 I t is taken =S2/n where n is aspect ratio as defined. Appendix II of Paper, I.c. ante.
17 The words “isospan” or “equispan,” which suggest themselves, savour too much of the hybrid.
18 These which include the tail plane, rudder, etc., present surfaces which are, roughly speaking, proportional to the aerofoil area.
19 “Aerodynamics,” Prop. IV, §165.
20 “Aerodynamics,” Prop. V, §166.
21 “Aerodynamics,” Prop. I, §164.
22 Loc. cit. ante.
23 At 48ft. span the loading will stand at very nearly 401bs./sq. ft., which may be regarded as inconveniently high, in view of the ground speed which would be necessary before take-off or when alighting. This means that for velocities at sea-level (or other specified level) greater than that in question, the optimum condition may not be capable of realisation: a compromise may be necessary. This would apply to all numbered K-span graphs shown in the chart higher than that in question.
24 In the data tabulated and plotted in Part IV of the author's recent paper, loc. cit. ante, it transpired that there is a loss of efficiency equivalent to about 5 per cent, in the case of an aerofoil selected as the best of those to which the records relate.
25 Or, 7,850 poundals. The pound unit of force is here employed, in view of the subsequent calculation of h.p. in which the familiar expression is used.


