No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 28 July 2016
For horizontal, or nearly horizontal, steady straight flight there exist some charts from which can be determined the speed at any altitude, the inclination of the flight path, and other quantities. This can be readily done, for instance, by a graphical comparison of the forces of drag and thrust, or by a corresponding representation of the powers, required and available. These charts, however, always involve the polar of the particular aeroplane, and are thus valid only for that aeroplane; they must therefore be replotted for each example. To avoid this and obtain a generally valid chart, the effect of the aerodynamic characteristics of the particular aeroplane must be eliminated; it is thus possible to prepare a chart even for the steady circling flight at any inclination of the flight path.
The three equations for the description of the flight path may be derived on the simple assumption that the thrust acts almost along the direction of flight, i.e., that the angles of attack and of sideslip are negligibly small.
Note on page 568 † This approximate formula for σ is derived from an essay of KnoUer in Flugsport, 1924, p. 309, and reproduces the Standard Atmosphere up to the altitude mentioned with less than 1 per cent, error; its inverse is h≃66, 1–≃/1+≃ valid down to ≃=0.3.
Note on page 569 * To determine this, it is necessary to know also the nature of the polar between CL for ra max and CL max’ which region is not covered by the usual parabolic formulae. It is found in many cases that the entire polar of the aeroplane can be represented by a quarter of an ellipse, which can be conveniently transformed into a quarter of a circle by suitably proportioning the scales for CD and CL. Given only CDo (at CL=0) and ra max and using a judicious estimate of CL max’ possible by choosing the ratio of the units for the CD- and CL-scales as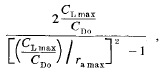 
to determine completely this “circular polar,” which forms a simple, sufficiently accurate, and reasonable basis for numerical computations (see, for instance. Fig. 3).
Note on page 570 * Chiefly after Jane's All The World's Aircraft 1950-1951 and 1952-1953.