Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-29T11:05:33.878Z Has data issue: false hasContentIssue false
  • English
  • Français

Determination of the Buckling Load of Struts with Successive Approximations

Published online by Cambridge University Press:  28 July 2016

J. Ratzersdorfer
Get access Rights & Permissions [Opens in a new window]

Extract

In cases of tapered struts with hinged or built-in ends where the exact determination of the buckling load is complicated it may be useful to apply a method of successive approximations.

Let us first consider a bar of the length l with hinged ends under the action of the compressive force P. The differential equation of the bending line becomes

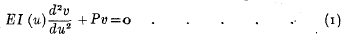
where v is the deflection at the section u, v with the moment of inertia I (u) and E is Young's modulus. At the ends of the bar the deflection v is equal to zero (Fig. I).

Type
Research Article
Information
The Aeronautical Journal , Volume 47 , Issue 387 , March 1943 , pp. 103 - 105
Copyright
Copyright © Royal Aeronautical Society 1943

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Note on page 103 * See also writer's book: Die Knickfestigkeit von Staben und Stabwerken (Buckling of Bars and Bar Systems), p. 117, Vienna, 193 , and his paper in R. Katzmayr's Beiträge zur Flugtechnik, p. 36, Vienna, 1937.

Note on page 105 * The accurate value has been calculated by A. N. Dinnik. Design of Columns of Varying Cross Sections. Transact. of the American Society of Mech. Engineers, 1928. Westnik Ingenerow, 1929