Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T07:17:46.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Metaheuristic data fitting methods to estimate Weibull parameters for wind speed data: a case study of Hasan Polatkan Airport

Published online by Cambridge University Press:  09 February 2021

A. Kaba Open the ORCID record for A. Kaba [Opens in a new window]  and
A. E. Suzer
A. Kaba*
Affiliation:
Faculty of Aeronautics and Astronautics, Eskişehir Technical University, 26555, Eskişehir, Turkey
A. E. Suzer
Affiliation:
Faculty of Aeronautics and Astronautics, Eskişehir Technical University, 26555, Eskişehir, Turkey
*
azizkaba@eskisehir.edu.tr
Get access Rights & Permissions [Opens in a new window]

Abstract

Flight delays may be decreased in a predictable way if the Weibull wind speed parameters of a runway, which are an important aspect of safety during the take-off and landing phases of aircraft, can be determined. One aim of this work is to determine the wind profile of Hasan Polatkan Airport (HPA) as a case study. Numerical methods for Weibull parameter determination perform better when the average wind speed estimation is the main objective. In this paper, a novel objective function that minimises the root-mean-square error by employing the cumulative distribution function is proposed based on the genetic algorithm and particle swarm optimisation. The results are compared with well-known numerical methods, such as maximum-likelihood estimation, the empirical method, the graphical method and the equivalent energy method, as well as the available objective function. Various statistical tests in the literature are applied, such as R2, Root-Mean-Square Error (RMSE) and 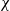$\chi$2. In addition, the Mean Absolute Error (MAE) and total elapsed time calculated using the algorithms are compared. According to the results of the statistical tests, the proposed methods outperform others, achieving scores as high as 0.9789 and 0.9996 for the R2 test, as low as 0.0058 and 0.0057 for the RMSE test, 0.0036 and 0.0045 for the MAE test and 3.53 × 10−5 and 3.50 × 10−5 for the 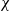$\chi$2 test. In addition, the determination of the wind speed characteristics at HPA show that low wind speed characteristics and regimes throughout the year offer safer take-off and landing schedules for target aircraft. The principle aim of this paper is to help establish the correct orientation of new runways at HPA and maximise the capacity of the airport by minimising flight delays, which represent a significant impediment to air traffic flow.

Keywords

Airport wind analysisWeibull distributionWind speedMetaheuristicsParameter estimationHasan Polatkan Airport
Type
Research Article
Information
The Aeronautical Journal , Volume 125 , Issue 1287 , May 2021 , pp. 916 - 948
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Royal Aeronautical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Genc, A., Erisoglu, M., Pekgor, A., Oturanc, G., Hepbasli, A. and Ulgen, K. Estimation of wind power potential using Weibull distribution, Energy Sources, 2005, 27, (9), pp 809–822. doi: 10.1080/00908310490450647.CrossRefGoogle Scholar
Ren21 Secretariat. Renewables 2019: Global Status Report, Paris. https://www.ren21.net/wp-content/uploads/2019/05/gsr_2019_full_report_en.pdf. Accessed 17 December 2019.Google Scholar
Alrashidi, M., Rahman, S. and Pipattanasomporn, M. Metaheuristic optimization algorithms to estimate statistical distribution parameters for characterizing wind speeds, Renew Energy, 2020, 149, pp 664–681. doi: 10.1016/j.renene.2019.12.048.Google Scholar
Mohsin, M. and Rao, K.V.S. Estimation of Weibull distribution parameters and wind power density for wind farm site at Akal at Jaisalmer in Rajasthan, 3rd International Conference on Innovative Applications of Computational Intelligence on Power, Energy and Controls with Their Impact on Humanity (CIPECH-18): 1st–2nd November 2018, Ghaziabad, India, 2018, pp 1–6.Google Scholar
Chang, T.P. Estimation of wind energy potential using different probability density functions, Appl Energy, 2011, 88, (5), pp 1848–1856. doi: 10.1016/j.apenergy.2010.11.010.CrossRefGoogle Scholar
Usta, I. An innovative estimation method regarding Weibull parameters for wind energy applications, Energy, 2016, 106, pp 301–314. doi: 10.1016/j.energy.2016.03.068.Google Scholar
Ouarda, T.B.M.J. et al.. Probability distributions of wind speed in the UAE, Energy Convers Manage, 2015, 93, pp 414–434. doi: 10.1016/j.enconman.2015.01.036.Google Scholar
Lo Brano, V., Orioli, A., Ciulla, G. and Culotta, S. Quality of wind speed fitting distributions for the urban area of Palermo, Italy, Renew Energy, 2011, 36, (3), pp 1026–1039. doi: 10.1016/j.renene.2010.09.009.CrossRefGoogle Scholar
Carta, J.A., Ramírez, P. and Velázquez, S. A review of wind speed probability distributions used in wind energy analysis: case studies in the Canary Islands, Renew Sustain Energy Rev, 2009, 13, (5), pp 933–955. doi: 10.1016/j.rser.2008.05.005.Google Scholar
Hu, Q., Wang, Y., Xie, Z., Zhu, P. and Yu, D. On estimating uncertainty of wind energy with mixture of distributions, Energy, 2016, 112, pp 935–962. doi: 10.1016/j.energy.2016.06.112.CrossRefGoogle Scholar
Ouarda, T.B.M.J. and Charron, C. On the mixture of wind speed distribution in a Nordic region, Energy Convers Manage, 2018, 174, pp 33–44. doi: 10.1016/j.enconman.2018.08.007.Google Scholar
Wais, P. Two and three-parameter Weibull distribution in available wind power analysis, Renew Energy, 2017, 103, pp 15–29. doi: 10.1016/j.renene.2016.10.041.CrossRefGoogle Scholar
Kantar, Y.M. and Usta, I. Analysis of the upper-truncated Weibull distribution for wind speed, Energy Convers Manage, 2015, 96, pp 81–88. doi: 10.1016/j.enconman.2015.02.063.CrossRefGoogle Scholar
Dong, Y., Wang, J., Jiang, H. and Shi, X. Intelligent optimized wind resource assessment and wind turbines selection in Huitengxile of Inner Mongolia, China, Appl Energy, 2013, 109, pp 239–253. doi: 10.1016/j.apenergy.2013.04.028.Google Scholar
Akdağ, S.A. and Dinler, A. A new method to estimate Weibull parameters for wind energy applications, Energy Convers Manage, 2009, 50, (7), pp 1761–1766. doi: 10.1016/j.enconman.2009.03.020.Google Scholar
Jiang, R. and Murthy, D.N.P. The exponentiated Weibull family: a graphical approach, IEEE Trans Rel, 1999 48, (1), pp 68–72. doi: 10.1109/24.765929.CrossRefGoogle Scholar
Chang, T.P. Performance comparison of six numerical methods in estimating Weibull parameters for wind energy application, Appl Energy, 2011, 88, (1), pp 272–282. doi: 10.1016/j.apenergy.2010.06.018.CrossRefGoogle Scholar
Balakrishnan, N. and Kateri, M. On the maximum likelihood estimation of parameters of Weibull distribution based on complete and censored data, Stat Probab Lett, 78, (17), pp 2971–2975, 2008, doi: 10.1016/j.spl.2008.05.019.Google Scholar
Costa Rocha, P.A., de Sousa, R.C., de Andrade, C.F. and da Silva, M.E.V. Comparison of seven numerical methods for determining Weibull parameters for wind energy generation in the northeast region of Brazil, Appl Energy, 2012, 89, (1), pp 395–400. doi: 10.1016/j.apenergy.2011.08.003.Google Scholar
Akdağ, S.A. and Güler, Ö. Alternative moment method for wind energy potential and turbine energy output estimation, Renew Energy, 2018, 120, pp 69–77. doi: 10.1016/j.renene.2017.12.072.CrossRefGoogle Scholar
Chen, W., Xie, M. and Wu, M. Modified maximum likelihood estimator of scale parameter using moving extremes ranked set sampling, Commun Stat Simul Comput, 2016, 45, (6), pp 2232–2240. doi: 10.1080/03610918.2014.904520.CrossRefGoogle Scholar
Akgül, F.G., Şenoğlu, B. and Arslan, T. An alternative distribution to Weibull for modeling the wind speed data: inverse Weibull distribution, Energy Convers Manage, 2016, 114, pp 234–240. doi: 10.1016/j.enconman.2016.02.026.CrossRefGoogle Scholar
Saleh, H., Abou El-Azm Aly, A. and Abdel-Hady, S. Assessment of different methods used to estimate Weibull distribution parameters for wind speed in Zafarana wind farm, Suez Gulf, Egypt, Energy, 2012, 44, (1), pp 710–719. doi: 10.1016/j.energy.2012.05.021.Google Scholar
Silva, G., Alexandre, P., Daniel, F. and Everaldo, F., Eds. On the Accuracy of the Weibull Parameters Estimators, 2004.Google Scholar
Rajabioun, R. Cuckoo optimization algorithm, Appl Soft Comput, 2011, 11, (8), pp 5508–5518. doi: 10.1016/j.asoc.2011.05.008.Google Scholar
Kennedy, J. and Eberhart, R. Particle swarm optimization, 1995 IEEE international conference on neural networks, Perth, WA, Australia, 1995, pp 1942–1948.Google Scholar
Cuevas, E., Cienfuegos, M., Zaldívar, D. and Pérez-Cisneros, M. A swarm optimization algorithm inspired in the behavior of the social-spider, Expert Syst Appl, 2013, 40, (16), pp 6374–6384. doi: 10.1016/j.eswa.2013.05.041.Google Scholar
Jiang, H., Wang, J., Wu, J. and Geng, W. Comparison of numerical methods and metaheuristic optimization algorithms for estimating parameters for wind energy potential assessment in low wind regions, Renew Sustain Energy Rev, 2017, 69, pp 1199–1217. doi: 10.1016/j.rser.2016.11.241.Google Scholar
Chang, T.P. Wind energy assessment incorporating particle swarm optimization method, Energy Convers Manage, 2011, 52, (3), pp 1630–1637. doi: 10.1016/j.enconman.2010.10.024.Google Scholar
Kumar, M.B.H., Balasubramaniyan, S., Padmanaban, S. and Holm-Nielsen, J.B. Wind energy potential assessment by Weibull parameter estimation using multiverse optimization method: a case study of Tirumala region in India, Energies, 2019, 12, (11), p 2158. doi: 10.3390/en12112158.CrossRefGoogle Scholar
Carneiro, T.C., Melo, S.P., Carvalho, P.C.M. and Braga, A. P. d. S. Particle Swarm Optimization method for estimation of Weibull parameters: a case study for the Brazilian northeast region, Renew Energy, 2016, 86, pp 751–759. doi: 10.1016/j.renene.2015.08.060.CrossRefGoogle Scholar
Yang, F., Ren, H. and Hu, Z. Maximum likelihood estimation for three-parameter Weibull distribution using evolutionary strategy, Math Prob Eng, 2019, 2019, pp 1–8. doi: 10.1155/2019/6281781.Google Scholar
Lu, Z., Dong, L. and Zhou, J. Nonlinear least squares estimation for parameters of mixed Weibull distributions by using particle swarm optimization, IEEE Access, 2019, 7, pp 60545–60554. doi: 10.1109/ACCESS.2019.2915279.CrossRefGoogle Scholar
Baklacioglu, T., Aydin, H. and Turan, O. Energetic and exergetic efficiency modeling of a cargo aircraft by a topology improving neuro-evolution algorithm, Energy, 2016, 103, pp 630–645. doi: 10.1016/j.energy.2016.03.018.CrossRefGoogle Scholar
Kaba, A. and Kyak, E. Optimizing a Kalman filter with an evolutionary algorithm for nonlinear quadrotor attitude dynamics, J Comput Sci, 2020, 39, p. 101051. doi: 10.1016/j.jocs.2019.101051.CrossRefGoogle Scholar
Baklacioglu, T., Turan, O. and Aydin, H. Dynamic modeling of exergy efficiency of turboprop engine components using hybrid genetic algorithm-artificial neural networks, Energy, 2015, 86, pp 709–721. doi: 10.1016/j.energy.2015.04.025.CrossRefGoogle Scholar
Kiyak, E. Tuning of controller for an aircraft flight control system based on particle swarm optimization, Aircr Eng Aerosp Technol, 2016, 88, (6), pp 799–809. doi: 10.1108/AEAT-02-2015-0037.CrossRefGoogle Scholar
Wang, J.-J. and Liu, G.-Y. Saturated control design of a quadrotor with heterogeneous comprehensive learning particle swarm optimization, Swarm Evol Comput, 2019, 46, pp 84–96. doi: 10.1016/j.swevo.2019.02.008.CrossRefGoogle Scholar
Yazar, I., Kiyak, E., Caliskan, F. and Karakoc, T.H. Simulation-based dynamic model and speed controller design of a small-scale turbojet engine, Aircr Eng Aerosp Technol, 2018, 90, (2), pp 351–358. doi: 10.1108/AEAT-09-2016-0150.CrossRefGoogle Scholar
Piskin, A., Baklacioglu, T., Turan, O. and Aydin, H. Modeling of energy efficiency of a turboprop engine using ant colony optimisation, Aeronaut J, 2020, 124, (1272), pp 237–256. doi: 10.1017/aer.2019.134.CrossRefGoogle Scholar
Tee, Y.Y. and Zhong, Z.W. Modelling and simulation studies of the runway capacity of Changi Airport, Aeronaut J, 2018, 122, (1253), pp 1022–1037. doi: 10.1017/aer.2018.48.CrossRefGoogle Scholar
Sahin, O. A proposed solution for airborne delays: linear holding, Aeronaut J, 2019, 123, (1269), pp 1840–1856. doi: 10.1017/aer.2019.78.Google Scholar
Daramola, A.Y. An investigation of air accidents in Nigeria using the Human Factors Analysis and Classification System (HFACS) framework, J Air Transp Manage, 2014, 35, pp 39–50. doi: 10.1016/j.jairtraman.2013.11.004.Google Scholar
Cecen, R.K., Cetek, C. and Kaya, O. Aircraft sequencing and scheduling in TMAs under wind direction uncertainties, Aeronaut J, 2020, 124, (1282), pp 1–17. doi: 10.1017/aer.2020.68.Google Scholar
Iijima, T., Matayoshi, N. and Ueda, S. Operational concept and validation of a new airport low-level wind information system, Aeronaut J, 2020, 124, (1277), pp 1–41, doi: 10.1017/aer.2020.9.CrossRefGoogle Scholar
Federal Aviation Administration (FAA). Advisory Circular AC 150/5300-13A: Airport Design, AC 150/5300-13A, 2014.Google Scholar
European Aviation Safety Agency (EASA). Authority, Organisation and Operations Requirements for Aerodromes, NPA 2011-20 (B.III), 2011.Google Scholar
International Civil Aviation Organization (ICAO). Runway Surface Condition Assessment, Measurement and Reporting, Cir 329/AN/191, 2012.Google Scholar
Es, G.W.H. and Karwal, A.K. Safety Aspects of Tailwind Operations, National Aerospace Laboratory (NLR) NLR-TP-2001-003, 2001.Google Scholar
Es, G.W.H., Geest, P.J. and Nieuwpoort, M.H. Safety Aspects of Aircraft Operations in Crosswind, National Aerospace Laboratory (NLR) NLR-TP-2001-217, 2001.Google Scholar
Kiran, D.R. Reliability Engineering, in Total Quality Management: Key Concepts and Case Studies, Kiran, D.R. (Ed.), Amsterdam, Boston: Elsevier, 2017, pp 391–404.Google Scholar
Siddiqui, A. et al.. Determination of Weibull parameter by four numerical methods and prediction of wind speed in Jiwani (Balochistan), J Basic Appl Sci, 2015, 11, pp 62–68. doi: 10.6000/1927-5129.2015.11.08.CrossRefGoogle Scholar
Rinne, H. The Weibull Distribution: A Handbook, CRC Press, 2009, Boca Raton, Florida, London.Google Scholar
Dagdougui, H., Ouammi, A. and Sacile, R. Towards a concept of cooperating power network for energy management and control of microgrids, Microgrid, M. S. Mahmoud (Ed.). Elsevier, 2017, pp 231–262.CrossRefGoogle Scholar
Turkish Statistical Institute. Population of Provinces by Years: Address Based Population Registration, 2019.Google Scholar
Technical University of Denmark. Global Wind Atlas 3.0: Web-Based Application.Google Scholar
Deaves, D.M. and Lines, I.G. On the fitting of low mean windspeed data to the Weibull distribution, J Wind Eng Ind Aerodyn, 1997, 66, (3), pp 169–178. doi: 10.1016/S0167-6105(97)00013-5.CrossRefGoogle Scholar
Mathew, S. Wind Energy: Fundamentals, Resource Analysis and Economics, Springer-Verlag Berlin Heidelberg, 2006, Berlin, Heidelberg.CrossRefGoogle Scholar
Kang, D., Ko, K. and Huh, J. Comparative study of different methods for estimating Weibull parameters: a case study on Jeju Island, South Korea, Energies, 2018, 11, (2), p. 356. doi: 10.3390/en11020356.CrossRefGoogle Scholar
Justus, C.G., Hargraves, W.R., Mikhail, A. and Graber, D. Methods for estimating wind speed frequency distributions, J Appl Meteor, 1978, 17, (3), pp 350–353. doi: .Google Scholar
Stevens, M.J.M. and Smulders, P.T. The estimation of the parameters of the Weibull wind speed distribution for wind energy utilization purposes, Wind Eng, 1979, 3, (2), pp 132–145. www.jstor.org/stable/43749134 Google Scholar
Singh, K., Bule, L., Khan, M.G.M. and Ahmed, M.R. Wind energy resource assessment for Vanuatu with accurate estimation of Weibull parameters, Energy Explor Exploit, 2019, 37, (6), pp 1804–1832, doi: 10.1177/0144598719866897.CrossRefGoogle Scholar
Haack, B.N. A simulation model for wind electric systems, Wind Eng, 1980, 4, (2), pp 64–75. www.jstor.org/stable/43749166 Google Scholar
Mani, A. and Mooley, D.A. Wind Energy Data for India. Allied Publishers, 1983, New Delhi, India. https://books.google.com.tr/books?id=9Ol1tgAACAAJ Google Scholar
Ahn, C.W. Advances in Evolutionary Algorithms: Theory, Design and Practice. Springer-Verlag Berlin Heidelberg, 2006. Berlin, Heidelberg. http://site.ebrary.com/lib/alltitles/docDetail.action?docID=10133682 Google Scholar
Chong, E.K.P. and Żak, S.H. An introduction to optimization, 3rd ed. Wiley Interscience, Hoboken, N.J.; John Wiley [distributor], Chichester, 2008. http://www.loc.gov/catdir/enhancements/fy0827/2007037112-b.html Google Scholar
Gümüşboğa, İ. and İftar, A. Aircraft trim analysis by particle swarm optimization, J Aeronaut Space Technol, 2019, 12, (2), pp 185–196.Google Scholar
Li, Z., Cui, J., Li, W. and Cui, Y. Three parameter Weibull distribution estimation based on particle swarm optimization, Proceedings of the 13th IEEE Conference on Industrial Electronics and Applications (ICIEA 2018): 31 May-2 June 2018 Wuhan, China, Wuhan, 2018, pp 1892–1899.CrossRefGoogle Scholar
Liu, B., Shi, C., Li, J., Li, Y., Lang, J. and Gu, R. Comparison of different machine learning methods to forecast air quality index, Frontier Computing: Theory, Technologies and Applications (FC 2017), J.C. Hung, N.Y. Yen and L. Hui (Eds.), Lecture Notes in Electrical Engineering, 1876–1100, Vol. 464. Springer, 2018, Singapore, pp 235–245.Google Scholar
Sürücü, B. Goodness-of-fit tests for multivariate distributions, Commun Stat Theory Methods, 2006, 35, (7), pp 1319–1331. doi: 10.1080/03610920600628999.CrossRefGoogle Scholar
Sürücü, B. A power comparison and simulation study of goodness-of-fit tests, Comput Math Appl, 2008, 56, (6), pp 1617–1625. doi: 10.1016/j.camwa.2008.03.010.CrossRefGoogle Scholar
Fürnkranz, J. et al.. Mean absolute error, Encyclopedia of Machine Learning, C. Sammut and G.I. Webb (Eds.), Springer, 2010, New York, London, p. 652.Google Scholar