No CrossRef data available.
Article contents
Numerical simulation of the pressure characteristics of the pulsed jet actuator
Published online by Cambridge University Press: 02 October 2023
Abstract
A compressible large eddy simulation (LES) is performed to study a pulsed jet actuator that is used to control a turbulent axisymmetric bluff body wake. The actuator is driven at low-frequency (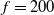 $f = 200$Hz,
$f = 200$Hz, 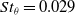 $S{t_\theta } = 0.029$) and high amplitude (
$S{t_\theta } = 0.029$) and high amplitude (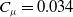 ${C_\mu } = 0.034$). The numerical scheme and a suitable boundary condition for the pulsed jet are validated, showing good agreement with experimental results. A comparison of the velocity boundary condition and the moving boundary condition shows that, in the vicinity of the orifice/slot and in the downstream region, the results from these two methods are identical, while the fluid behaviour inside the cavity shows difference. An analysis of the pulsed jet actuator shows that the phase lag of the cavity pressure is determined by the integration of the diaphragm motion and the pulsed jet. The mean total pressure distribution shows that the total pressure loss is concentrated in the vicinity of the slot. Dynamic mode decomposition (DMD) on the pressure field is used to extract coherent structures which oscillate with the same frequency as that of the diaphragm motion. Some small-scale high-frequency structures are also apparent.
${C_\mu } = 0.034$). The numerical scheme and a suitable boundary condition for the pulsed jet are validated, showing good agreement with experimental results. A comparison of the velocity boundary condition and the moving boundary condition shows that, in the vicinity of the orifice/slot and in the downstream region, the results from these two methods are identical, while the fluid behaviour inside the cavity shows difference. An analysis of the pulsed jet actuator shows that the phase lag of the cavity pressure is determined by the integration of the diaphragm motion and the pulsed jet. The mean total pressure distribution shows that the total pressure loss is concentrated in the vicinity of the slot. Dynamic mode decomposition (DMD) on the pressure field is used to extract coherent structures which oscillate with the same frequency as that of the diaphragm motion. Some small-scale high-frequency structures are also apparent.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Royal Aeronautical Society
Footnotes
Current affiliation at Shanghai Automotive Wind Tunnel Center, Tongji University and School of Automotive Studies, Tongji University and Shanghai Key Lab of Vehicle Aerodynamics and Vehicle Thermal Management Systems.


