No CrossRef data available.
Article contents
Part III. Local Buckling of Monocoque Structures
Published online by Cambridge University Press: 28 July 2016
Extract
In case of normal monocoque aeroplane fuselages relatively strong rings are spaced at distances equal to 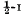 diameter of the fuselage, failure of the structure always occurs by instability of the most stressed stringer. The buckling stress, however, is mostly very low, especially, when the number of stringers is great and consequently the cross section of one stringer is small. The value of the stress at failure may be raised by spacing the rings nearer and reducing thereby the free length and, consequently, the slenderness ratio of the stringers. In this case the rings should be constructed of lighter sections in order to balance the increment of weight of the whole structure due to the greater number of rings.
diameter of the fuselage, failure of the structure always occurs by instability of the most stressed stringer. The buckling stress, however, is mostly very low, especially, when the number of stringers is great and consequently the cross section of one stringer is small. The value of the stress at failure may be raised by spacing the rings nearer and reducing thereby the free length and, consequently, the slenderness ratio of the stringers. In this case the rings should be constructed of lighter sections in order to balance the increment of weight of the whole structure due to the greater number of rings.
By decreasing gradually the interval between rings a critical distance is reached when the most stressed stringer does not buckle between adjacent rings, but forces one or more supporting rings to deform simultaneously. This form of instability will in the following be termed local buckling of the monocoque structure.
Information
- Type
- Instability of Monocoque Structures in Pure Bending
- Information
- Copyright
- Copyright © Royal Aeronautical Society 1938
References
35 V. Ref. 7.
36 The minimum condition of the function
P or=F(x)=A(x)/B(x)
is given by
dF(x)/dx=[dA(x)/dx]/B(x)–[dB(x)/dx][A(x)/B 2(x)]=0
or
[dA(x)/dx]–[A(x)/B(x)][dB(x)/dx]=0.
This equation may be transformed into
P or=[dA(x)/dx]/[dB(x)/dx].
37 Cf. §3 of Ref. 8.

