Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T06:32:04.886Z Has data issue: false hasContentIssue false
  • English
  • Français

A Two-Parameter Method for Calculating the Two-Dimensional Incompressible Laminar Boundary Layer

Published online by Cambridge University Press:  04 July 2016

N. Curle
N. Curle*
Affiliation:
Mathematics Department, University of Southampton
Get access Rights & Permissions [Opens in a new window]

Summary:

In most one-parameter methods of calculating laminar boundary layers it is assumed that the non-dimensional parameters H=δ1/δ2, I=δ2τW/μu1 and L = 2{I−λ(H+2)}, depend only upon the pressure gradient parameter λ=u1δ22/v. In this paper it is shown theoretically that a more accurate, two-parameter representation is

L=F0(λ)−μG0(λ)

I2=F1(λ)−μG1(λ),

where μ=λ2U1U1/(U1)2. Careful examination of the available range of exact solutions of the boundary layer equations has enabled the four functions F0, G0, F1, G1, to be tabulated, and the above functional forms agree with the exact solutions to a remarkable accuracy.

In view of the fact that a reasonable first approximation to L is usually 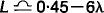, we write

,

and it is then shown that the momentum integral equation becomes

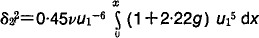
This equation is easily solved by iteration, setting g=0 in the first approximation, and convergence is extremely rapid.

The method is, in effect, a refinement of that due to Thwaites, which is universally accepted as one of the better of the existing calculation methods. Detailed calculations made by the present method indicate that the errors are only 5% of those given by the Thwaites method.

Type
Research Article
Information
The Aeronautical Journal , Volume 71 , Issue 674 , February 1967 , pp. 117 - 123
Copyright
Copyright © Royal Aeronautical Society 1967

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Rosenhead, L. (Ed). Laminar Boundary Layers. OUP, 1963.Google Scholar
2.Curle, N.The Laminar Boundary Layer Equations. OUP, 1962.Google Scholar
3.Illingworth, C. R.Steady Flow in the Laminar Boundary Layer of a Gas. Proc Roy Soc A 199, p 533, 1949.Google Scholar
4.Stewartson, K.Correlated Incompressible and Compressible Boundary Layers. Proc Roy Soc A 200, p 84, 1949.Google Scholar
5.Curle, N.The Steady Compressible Laminar Boundary Layer, with Arbitrary Pressure Gradient and Uniform Wall Temperature. Proc Roy Soc A 249, p 206, 1958.Google Scholar
6.Morduchow, M. and Reyle, S. P.On the Calculation of the Laminar Separation Point, and Results for Certain Flows. Journ Aerospace Soc, Vol 29, p 996, 1962.Google Scholar
7.Head, M. R. An Approximate Method for Calculating the Laminar Boundary Layer in Two-Dimensional Incom pressible Flow. ARC R and M 3123, 1957.Google Scholar
8.Tani, I.On the Approximate Solution of the Laminar Boundary Layer Equations. Journ Aerospace Soc, Vol 21, p 487, 1954.Google Scholar
9.Truckenbrodt, E.Ein quadraturrerfahren zur berechnung der laminaren und turbulenten reibungsschichten bei ebener und rotationssymmetrischer stromung. Ingenieur Archiv, Vol 20, p 211,1952.Google Scholar