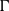Verification & validation of lifting line $\alpha $- and $\Gamma $-formulations for 3-D planforms under viscous flows

Abstract

Many adaptations of the lifting-line theory have been developed since its conception to aid in preliminary aerodynamic wing design, but they typically fall into two main formulations, named $\alpha $- and 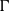$\Gamma $-formulation, which differ in terms of the control points chordwise location and the variable updated during the iterative scheme. This paper assess the advantages and drawbacks of both formulations through the implementation of the respective methods and application of standard verification and validation procedures. Verification showed that the 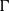$\Gamma $-method poorly converges for wings with nonstraight quarter-chord lines, while the $\alpha $-method presents adequate convergence rates and uncertainties for all geometries; it also showed that the 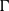$\Gamma $-method agrees best with analytic results from the cassic lifting-line theory, indicating that it tends to overpredict wing lift. Validation and comparison to other modern lifting-line methods was done for similar geometries, and not only corroborated the poor converge and lift overprediction of the $\Gamma $-method, but also showed that the $\alpha $-method presented the closest results to experimental data for almost all cases tested, concluding that this formulation is typically superior regardless of the wing geometry. These results indicate that the implemented $\alpha $-method has a greater potential for the extension of the lifting-line theory to more geometrically complex lifting surfaces other than fixed wings with straight quarter-chord lines and wakes constrained to the planform plane.

Nomenclature

A

constant of the function obtained with the Richardson extrapolation

AR

aspect ratio

b

wing span

c

aerofoil chord/wing chord at a given spanwise location

$\bar c$

mean aerodynamic chord

${C_d}$

aerofoil drag coefficient

${C_D}$

wing drag coefficient

${C_l}$

aerofoil lift coefficient

${C_L}$

wing lift coefficient

${\epsilon _{{C_L}}}$

absolute error for the wing lift coefficient

${\bf{F}}$

aerodynamic force

h

representative grid size

$\mathbb{J}$

Jacobian matrix

${\bf{l}}$

bound vortex length vector

$\mathbb{M}$

influence matrix

${M_{ij}}$

influence matrix $i{j^{{\rm{th}}}}$ element

N

number of horseshoe vortices/control points

P

order of convergence of the Richardson extrapolation

${\bf{r}}$

vector connecting the edge of the horseshoe vortex to a point in space

R

array of residues

Re

Reynolds number

S

planform area

${{\bf{u}}_n}$

aerofoil normal unit vector

${U_h}$

grid numerical uncertainty

${\bf{v}}$

unit velocity vector

${\bf{V}}$

velocity vector

W

normal velocity component

y

spanwise direction

Greek symbol

$\alpha $

angle-of-attack

$\delta $

relative to section

$\Delta $

variation

$\Gamma $

circulation

$\Omega $

relaxation factor

$\rho $

density

$\theta $

geometric twist/Zero lift angle-of-attack

Subscripts and Superscripts

$\infty $

free-stream

BV

bound vortex

CLL

classical lifting-line

CP

control point

eff

effective

HSV

horseshoe vortex

i,j

pertaining to ${{\rm{i}}^{{\rm{th}}}}/{{\rm{j}}^{{\rm{th}}}}$ section

k

referring to the horseshoe vortex ${{\rm{k}}^{{\rm{th}}}}$ edge

L0

zero-lift

n

${{\rm{n}}^{{\rm{th}}}}$ time-step

rot

rotation

TV

trailing Vortex

Vis

real aerofoil data

ws

wing section

1.0 Introduction

Wing aerodynamic design is one of the most benefited fields from the later development of computational fluid dynamics (CFD), here referring to schemes that solve the Navier-Stokes equations through either finite volumes, finite elements, finite differences or spectral methods, due to their accuracy for flows ranging from low [1] to high [2] Reynolds numbers; however, they currently present a drawback in computational cost as a full simulation ranges from hours to days in modern supercomputers. This bottleneck limits the application of CFD during early design phases as many flow and geometric features must be assessed, so its use is more convenient when higher resolution is needed.

Modern lifting-line (LL) methods, on the other hand, have a balance between cost and accuracy that make them attractive for early design, as it is possible to evaluate many wing and flow configurations at a much lower cost while retaining adequate fidelity. This characteristic broadened application to lifting surfaces other than wings, such as kites [3], hydrofoils [4], wind turbines [5], and marine propellers [6] to name a few. Even time-dependent flows [7, 8] and LL-CFD coupling [9–11] have been shown to be advantageous due to the significantly reduced computational cost yet relatively high flow topological detail.

Li et al. [8] used aerofoil data from CFD on an unsteady LL formulation to estimate wing aerodynamic forces in preliminary design phase, obtaining good agreement with full 3-D unsteady CFD calculations in less than a tenth of the time. Likewise, Şugar-Gabor and Koreanschi [12] integrated a modern LL formulation into a simultaneous analysis and design methodology and showed that good accuracy was achieved at relatively low computational time, making it appropriate for conceptual-level design and optimisation of lifting geometries.

Modern LL methods have been mainly divided into two formulations: $\alpha $ -formulations, which iteratively solve the system of nonlinear equations through changes in the effective angle-of-attack (AoA) ${\alpha _{eff}}$ , and $\Gamma $ -formulations, which do so through changes in the circulation distribution $\Gamma $ . But the maturing of numerical methods for practical applications ultimately make them subject to quality and reliability assessment, and verification and validation (V&V) is one of the most-used procedures for such purpose. While verification is a mathematical exercise that shows the modeled equations are solved correctly, validation is a science/engineering activity that shows what is being solved are the correct model equations [13], so V&V is a crucial procedure to the development and improvement of any numerical method.

Therefore, this paper summarises implementations of $\alpha $ - and $\Gamma $ -methods for wings and contrasts them through standard V&V procedures [13–15] for a series of geometries of interest. They are also compared against other implementations in the literature, which are different flavors of either formulations or a combination of the two. Results showed that, for most planforms tested, the $\Gamma $ -method tends to overpredict wing lift in comparison to experiments, while the $\alpha $ -method typically has better convergence stability and overall agreement with experimental data.

2.0 The $\alpha $ and $\Gamma $ lifting-line theory of wings

The original LL theory was crucial to the advance of modern aerodynamics [16, 17] and the need for wings with arbitrary geometries at optimum aerodynamic efficiency motivated its improvement; Weissinger’s lifting-line [18], for example, extended the theory to wings with nonstraight quarter-chord $\dfrac{c}{4}$ lines by forcing each discretised section to satisfy Pistolesi’s boundary condition [19] (PBC) at the third quarter chord location $\dfrac{{3c}}{4}$ , and inclusion of real aerofoil data through iterative schemes date back to at least the 1950s [20].

Mainly two LL formulations arose from these improvements [8, 21], and the following classification is used herein: (i) $\Gamma $ -formulations, referring to those whose bound vortices (BVs) and control points (CPs) are both placed over the $\dfrac{c}{4}$ line, as in Fig. 1, while the iterative scheme updates $\Gamma $ , and (ii) $\alpha $ -formulations, referring to those whose BV and CP are placed at $\dfrac{c}{4}$ and $\dfrac{{3c}}{4}$ lines, respectively, as in Fig. 2, while the iterative scheme updates ${\alpha _{eff}}$ . According to such classification, there are also (iii) ‘mixed’-formulations, referring to those whose BV-CP follow the $\alpha $ -formulation, but the iterative procedure follows the $\Gamma $ -formulation [22], which eventually relaxes the PBC.

Figure 1. Horseshoe vortex wing representation for the $\Gamma $ -method.

Figure 2. Horseshoe vortex wing representation for the $\alpha $ -method.

An acclaimed $\Gamma $ -formulation was presented by Phillips & Snyder [23], who replaced the continuous horseshoe vortex (HSV) distribution by a finite number of discrete vortices in a vortex-lattice representation [17] and included real aerofoil data through the knowledge of ${\alpha _{eff}}$ . The obtained aerofoil lift coefficient ${C_l}$ would be compared against its potential estimates from a combination of the Kutta–Joukowski theorem (KJT) [24] and its mathematical definition, and if the two differed, $\Gamma $ would be iteratively updated through a Newton’s scheme until they matched to a certain tolerance. Likewise, an example of $\alpha $ -formulation is presented in Chreim et al. [25], whose discretisation, ${C_l}$ calculations, and convergence criterion are similar to the $\Gamma $ -method, but with a different iterative scheme, as ${\alpha _{eff}}$ is recalculated [26] through changes in the chordwise CP locations [27, 28], forcing $\Gamma $ to be such that the induced velocities satisfy the PBC. In the next subsections, both formulations will be summarised.

2.1 The $\Gamma $ -method

For the sake of discussion on the differences between the two main LL formulations, a $\Gamma $ -formulation (herein called $\Gamma $ -method) originally proposed by Phillips & Snyder [23] is summarised in this subsection. Consider a wing and its wake represented by N HSVs, as in Fig. 1. The velocity ${\bf{V}}_{ij}^{HSV}$ induced at any ${{\textrm{i}}^{{\textrm{th}}}}$ CP in space by a ${{\textrm{j}}^{{\textrm{th}}}}$ HSV with circulation ${\Gamma _j}$ is calculated by Equation (1):

(1) \begin{align}{\bf{V}}_{ij}^{HSV} = - \frac{{{\Gamma _j}}}{{4\pi }}\left[ {\frac{{{{\bf{v}}_\infty } \times {\bf{r}}_{ij}^{\left( 2 \right)}}}{{r_{ij}^{\left( 2 \right)}(r_{ij}^{\left( 2 \right)} - {{\bf{v}}_\infty } \cdot {\bf{r}}_{ij}^{\left( 2 \right)})}} - \frac{{(r_{ij}^{\left( 2 \right)} + r_{ij}^{\left( 3 \right)})({\bf{r}}_{ij}^{\left( 2 \right)} \times {\bf{r}}_{ij}^{\left( 3 \right)})}}{{r_{ij}^{\left( 2 \right)}r_{ij}^{\left( 3 \right)}(r_{ij}^{\left( 2 \right)}r_{ij}^{\left( 3 \right)} + {\bf{r}}_{ij}^{\left( 2 \right)} \cdot {\bf{r}}_{ij}^{\left( 3 \right)})}} + \frac{{{\bf{r}}_{ij}^{\left( 3 \right)} \times {{\bf{v}}_\infty }}}{{r_{ij}^{\left( 3 \right)}(r_{ij}^{\left( 3 \right)} - {{\bf{v}}_\infty } \cdot {\bf{r}}_{ij}^{\left( 3 \right)})}}} \right]\end{align}

in which ${\bf{r}}_{ij}^{\left( k \right)} = \left( {{x_{cp,i}} - x_{bv,j}^{\left( k \right)},{y_{cp,i}} - y_{bv,j}^{\left( k \right)},{z_{cp,i}} - z_{bv,j}^{\left( k \right)}} \right)$ is the vector connecting the ${{\textrm{k}}^{{\textrm{th}}}}$ edge (for consistency with the $\alpha $ -method, $k = 2,3$ ) of the ${{\textrm{j}}^{{\textrm{th}}}}$ BV, located at $\left( {x_{bv,j}^{\left( k \right)},y_{bv,j}^{\left( k \right)},z_{bv,j}^{\left( k \right)}} \right)$ , to the ${{\textrm{i}}^{{\textrm{th}}}}$ CP, located at $\left( {{x_{cp,i}},{y_{cp,i}},{z_{cp,i}}} \right)$ , and ${{\bf{v}}_\infty }$ is the free-stream unit velocity vector. The overall velocity ${{\bf{V}}_i}$ at this CP is the superposition of the free stream ${{\bf{V}}_\infty }$ , the $N - 1$ induced velocities from the other HSVs, and the induced velocities by i itself minus the BV component:

(2) \begin{align}{{\bf{V}}_i} = {{\bf{V}}_\infty } - \frac{{{\Gamma _i}}}{{4\pi }}\left[ {\frac{{{{\bf{v}}_\infty } \times {\bf{r}}_{ii}^{\left( 2 \right)}}}{{r_{ii}^{\left( 2 \right)}(r_{ii}^{\left( 2 \right)} - {{\bf{v}}_\infty } \cdot {\bf{r}}_{ii}^{\left( 2 \right)})}} + \frac{{{\bf{r}}_{ii}^{\left( 3 \right)} \times {{\bf{v}}_\infty }}}{{r_{ii}^{\left( 3 \right)}(r_{ii}^{\left( 3 \right)} - {{\bf{v}}_\infty } \cdot {\bf{r}}_{ii}^{\left( 3 \right)})}}} \right] + \sum\limits_{j = 1,j \ne i}^N {\bf{V}}_{ij}^{HSV}\end{align}

The aerodynamic force $\delta {{\bf{F}}_i}$ normal to ${{\bf{V}}_i}$ and the BV length vector $\delta {{\bf{l}}_i}$ is obtained through the KJT:

(3) \begin{align}\delta {{\bf{F}}_i} = {\rho _\infty }{\Gamma _i}{{\bf{V}}_i} \times \delta {{\bf{l}}_i}\end{align}

with ${\rho _\infty }$ the free-stream density. Likewise, its magnitude can be expressed through the definition of the section lift coefficient ${C_l}$ :

(4) \begin{align}\delta {F_i} = \frac{1}{2}{\rho _\infty }V_\infty ^2{C_{l,i}}\delta {S_i}\end{align}

with $\delta {S_i}$ the ${{\textrm{i}}^{{\textrm{th}}}}$ wing section area. Combining Equations (3) and (4):

(5) \begin{align}{C_{l,i}} = 2\left( {\frac{{{\Gamma _i}}}{{{{\bar c}_i}{V_\infty }}}} \right)\left| {\frac{{{{\bf{V}}_i}}}{{{V_\infty }}} \times \frac{{{{\bar c}_i}\delta {{\bf{l}}_i}}}{{\delta {S_i}}}} \right|\end{align}

in which ${\bar c_i}$ is a mean characteristic chord for purposes of nondimensionalisation. Expression (5) is compared against real aerofoil lift coefficient $C_{l,i}^{Vis}\left( {{\alpha _{eff,i}}} \right)$ from either experiments, simulations, or analytic/semi-empirical curves:

(6) \begin{align}{C_{l,i}} - C_{l,i}^{Vis}\left( {{\alpha _{eff,i}}} \right) = {R_i}\end{align}

with ${R_i}$ the residue that is ideally 0 and ${\alpha _{eff,i}}$ calculated from ${{\bf{V}}_i}$ [23]. Equation (6) provides a system of N nonlinear equations that is iteratively solved for $\boldsymbol\Gamma \equiv \left( {{\Gamma _1},{\Gamma _2}, \cdots ,{\Gamma _N}} \right)$ and stops when ${\bf{R}} \equiv \left( {{R_1},{R_2}, \cdots ,{R_N}} \right) \approx {\bf{0}}$ . With an adequate initial guess, from the linearised version of Equation (6), the method rapidly converges via Newton’s method:

(7) \begin{align}\mathbb{J}\left( \frac{{\boldsymbol\Delta \boldsymbol\Gamma }}{{{\bar{\textbf{c}}{V_\infty }}}} \right) = - {\bf{R}}\end{align}

(8) \begin{align}{\boldsymbol\Gamma ^{{\bf{n}} + {\bf{1}}}} = {\boldsymbol\Gamma ^{\bf{n}}} + \Omega \bar{\textbf{c}}{V_\infty }\left( {\frac{{\Delta \Gamma }}{{\bar{\textbf{c}}{V_\infty }}}} \right)\quad \Omega \in \left( {0,1} \right]\end{align}

with $\mathbb{J}$ the Jacobian matrix and $\Omega $ a subrelaxation factor (typically 0.8). The total aerodynamic forces, moments and coefficients can be determined by numerically integrating Equation (4), but the current discussion is limited to the lift and drag coefficients ${C_L}$ and ${C_D}$ . At this point, the aerofoil drag coefficient ${C_{d,i}}$ can be included:

(9) \begin{align}{C_L}& = \frac{1}{{V_\infty ^2S}}\sum\limits_{i = 1}^N V_i^2\delta {S_i}\left[ {{C_{l,i}}\cos \!\left( {{\alpha _{rot,i}}} \right) - {C_{d,i}}\sin \!\left( {{\alpha _{rot,i}}} \right)} \right]\notag\\ {C_D} & = \frac{1}{{V_\infty ^2S}}\sum\limits_{i = 1}^N V_i^2\delta {S_i}\left[ {{C_{l,i}}\sin \!\left( {{\alpha _{rot,i}}} \right) + {C_{d,i}}\cos \!\left( {{\alpha _{rot,i}}} \right)} \right]\end{align}

in which ${\alpha _{rot}}$ is a rotation angle relating aerofoil and wing coordinate systems, and includes the geometric twist, zero-lift and induced angles. The $\Gamma $ -method yields adequate results for regions up to stall and planforms whose $\dfrac{c}{4}$ are straight; grid convergence analysis indicates, however, convergence issues for $\dfrac{c}{4}$ lines with sweep angles [29–31], so recent work [32, 33] adapted the method to overcome this drawback.

2.2 The $\alpha $ -method

Again, to highlight the differences between the two main formulations, an $\alpha $ -formulation (herein called $\alpha $ -method), proposed by Chreim et al. [25], is summarised in this subsection. The chosen HSV geometry is depicted in Fig. 2, and Equation (1) is adjusted accordingly:

(10) \begin{align} {\bf{V}}_{ij}^{HSV} & = - \frac{{{\Gamma _j}}}{{4\pi }}\left[\frac{{{{\bf{v}}_\infty } \times {\bf{r}}_{ij}^{\left( 1 \right)}}}{{r_{ij}^{\left( 1 \right)}(r_{ij}^{\left( 1 \right)} - {{\bf{v}}_\infty } \cdot {\bf{r}}_{ij}^{\left( 1 \right)})}} - \frac{{(r_{ij}^{\left( 1 \right)} + r_{ij}^{\left( 2 \right)})({\bf{r}}_{ij}^{\left( 1 \right)} \times {\bf{r}}_{ij}^{\left( 2 \right)})}}{{r_{ij}^{\left( 1 \right)}r_{ij}^{\left( 2 \right)}(r_{ij}^{\left( 1 \right)}r_{ij}^{\left( 2 \right)} + {\bf{r}}_{ij}^{\left( 1 \right)} \cdot {\bf{r}}_{ij}^{\left( 2 \right)})}}\right.\notag\\ & \quad \left.- \frac{{(r_{ij}^{\left( 2 \right)} + r_{ij}^{\left( 3 \right)})({\bf{r}}_{ij}^{\left( 2 \right)} \times {\bf{r}}_{ij}^{\left( 3 \right)})}}{{r_{ij}^{\left( 2 \right)}r_{ij}^{\left( 3 \right)}(r_{ij}^{\left( 2 \right)}r_{ij}^{\left( 3 \right)} + {\bf{r}}_{ij}^{\left( 2 \right)} \cdot {\bf{r}}_{ij}^{\left( 3 \right)})}} - \frac{{(r_{ij}^{\left( 3 \right)} + r_{ij}^{\left( 4 \right)})({\bf{r}}_{ij}^{\left( 3 \right)} \times {\bf{r}}_{ij}^{\left( 4 \right)})}}{{r_{ij}^{\left( 3 \right)}r_{ij}^{\left( 4 \right)}(r_{ij}^{\left( 3 \right)}r_{ij}^{\left( 4 \right)} + {\bf{r}}_{ij}^{\left( 3 \right)} \cdot {\bf{r}}_{ij}^{\left( 4 \right)})}} + \frac{{{\bf{r}}_{ij}^{\left( 4 \right)} \times {{\bf{v}}_\infty }}}{{r_{ij}^{\left( 4 \right)}(r_{ij}^{\left( 4 \right)} - {{\bf{v}}_\infty } \cdot {\bf{r}}_{ij}^{\left( 4 \right)})}}\right]\end{align}

Likewise, ${{\bf{V}}_i}$ now considers the contribution of all $5N$ segments:

(11) \begin{align}{{\bf{V}}_i} = {{\bf{V}}_\infty } + \sum\limits_{j = 1}^N {\bf{V}}_{ij}^{HSV}\end{align}

The $\alpha $ -method requires the enforcement of the PBC [19]:

(12) \begin{align}{{\bf{u}}_{n,i}} \cdot {{\bf{V}}_i} = 0 \to \sum\limits_{j = 1}^N {{\bf{u}}_{n,i}} \cdot {\bf{V}}_{ij}^{HSV} = - {{\bf{u}}_{n,i}} \cdot {{\bf{V}}_\infty }\end{align}

with ${{\bf{u}}_{n,i}}$ the ${{\textrm{i}}^{{\textrm{th}}}}$ normal unit vector; unlike the $\Gamma $ -method, the $\alpha $ -method does not require a force equivalence, but rather this no-flux condition at the CPs [19]. Equation (12) can be cast into a matrix form:

(13) \begin{align}\mathbb{M}\boldsymbol\Gamma = - {{\bf{W}}_\infty }\end{align}

with:

(14) \begin{align}{M_{ij}} = {{\bf{u}}_{n,i}} \cdot {\bf{V}}_{ij}^{HSV};\quad {W_{\infty ,i}} = {{\bf{u}}_{n,i}} \cdot {{\bf{V}}_\infty }\end{align}

Note that Equation (13) is nonlinear as $\mathbb{M}$ depends on the CP locations, which depend on $C_l^{Vis}$ , so $\boldsymbol\Gamma $ must be solved iteratively as follows: after a first estimate for $\boldsymbol\Gamma $ , whose initial guess comes from assuming ${x_{cp,i}} = \dfrac{3}{4}{c_i}\;\forall i = 1, \cdots ,N$ (implying $\dfrac{{\partial {C_{l,i}}}}{{\partial {\alpha _i}}} = 2\pi $ ) ${C_{l,i}}$ is calculated through Equation (5), but with ${{\bf{V}}_i}$ and ${{\bf{V}}_\infty }$ replaced by the velocity ${\bf{V}}_i^{{C_l}}$ induced by only the attached and free trailing vortices [17] plus the free-stream:

(15) \begin{align}{\bf{V}}_i^{{C_l}} = {{\bf{V}}_\infty } + \sum\limits_{j = 1}^N {\bf{V}}_{ij}^{TV}\end{align}

\begin{align*}{\bf{V}}_{ij}^{TV} & = - \frac{{{\Gamma _j}}}{{4\pi }}\left[ {\frac{{{{\bf{v}}_\infty } \times {\bf{r}}_{ij}^{\left( 1 \right)}}}{{r_{ij}^{\left( 1 \right)}(r_{ij}^{\left( 1 \right)} - {{\bf{v}}_\infty } \cdot {\bf{r}}_{ij}^{\left( 1 \right)})}} - \frac{{(r_{ij}^{\left( 1 \right)} + r_{ij}^{\left( 2 \right)})({\bf{r}}_{ij}^{\left( 1 \right)} \times {\bf{r}}_{ij}^{\left( 2 \right)})}}{{r_{ij}^{\left( 1 \right)}r_{ij}^{\left( 2 \right)}(r_{ij}^{\left( 1 \right)}r_{ij}^{\left( 2 \right)} + {\bf{r}}_{ij}^{\left( 1 \right)} \cdot {\bf{r}}_{ij}^{\left( 2 \right)})}}}\right.\notag\\ & \qquad \qquad\left.{ - \frac{{(r_{ij}^{\left( 3 \right)} + r_{ij}^{\left( 4 \right)})({\bf{r}}_{ij}^{\left( 3 \right)} \times {\bf{r}}_{ij}^{\left( 4 \right)})}}{{r_{ij}^{\left( 3 \right)}r_{ij}^{\left( 4 \right)}(r_{ij}^{\left( 3 \right)}r_{ij}^{\left( 4 \right)} + {\bf{r}}_{ij}^{\left( 3 \right)} \cdot {\bf{r}}_{ij}^{\left( 4 \right)})}} + \frac{{{\bf{r}}_{ij}^{\left( 4 \right)} \times {{\bf{v}}_\infty }}}{{r_{ij}^{\left( 4 \right)}(r_{ij}^{\left( 4 \right)} - {{\bf{v}}_\infty } \cdot {\bf{r}}_{ij}^{\left( 4 \right)})}}} \right]\end{align*}

If ${C_{l,i}}$ differs from $C_{l,i}^{Vis}$ , the ${{\textrm{i}}^{{\textrm{th}}}}$ CP location is adjusted, effectively changing ${\bf{r}}_{ij}^{\left( k \right)}$ and consequently ${{\bf{V}}_i}$ or, equivalently, ${\alpha _{eff,i}}$ , as the slope of the ${C_{l,i}} \times \alpha $ curve $\frac{{\partial {C_{l,i}}}}{{\partial {\alpha _i}}}$ changes [17]. After, $\boldsymbol\Gamma $ is updated. Mathematically, this happens according to the procedure indicated on Table 1 in which $\Omega $ is again typically 0.8. Table 1 shows that the the viscous curve is approximated by a linear interpolation, while the potential ${C_l} \times \alpha $ curve is iteratively adjusted based on $C_l^{Vis} \times \alpha $ . The iterative scheme is illustrated in Fig. 3, which stops when ${\bf{R}} \approx {\bf{0}}$ . The aerodynamic coefficients are obtained through Equation (9).

Table 1. Iterative solution procedure for the $\alpha $ -method

Figure 3. Illustrative example of the inclusion of real aerofoil data on the $\alpha $ -method.

As a final note, the vortex-lattice representation is advantageous as it easily enables the construction of wings with arbitrary shape as, contrary to formulations that approximate the circulation distribution by a Fourier series [21, 26], no parametric curve or arclength is needed to generate the geometry but rather information about the wing chord length at a given spanwise location. Additionally, this representation requires the CP locations to change [28, 34] rather than ${\alpha _{eff}}$ directly [21, 26]; simply changing ${\alpha _{eff}}$ in this formulation would not adjust the ${C_l} \times \alpha $ curve slope [27], so the only possible solution would be ${\alpha _{eff}} = {\alpha _{L0}}$ . It is also important to ensure that the CPs remain co-planar to the wing planform [31].

3.0 Results from verification and validation

In this section, both $\alpha $ - and $\Gamma $ -methods prediction capabilities are assessed through standard verification and validation (V&V) procedures [15]; after error and uncertainty estimation, they are compared against experimental results and other implementations from the literature.

Verification, presented in Section 3.1, is composed by Code and Solution Verification, intended to verify that a given code correctly solves the equations of the model and to estimate numerical error $\epsilon_{\phi}$ and uncertainty ${U_N}$ that arise from discretisation, iteration and numerical precision. To this end, different planform geometries were assessed for grid convergence, and those with existing analytic solutions were further assessed to measure how much both methods deviate from the classic theory.

Validation, presented in Section 3.2, aims to estimate the extent within which modeling error lies, accomplished by comparison with experimental data for a wide range of numerical testing conditions. Similar planform geometries were validated, and the methods were further compared to other state-of-the-art implementations.

The importance of V&V in the reliability of LL methods is illustrated by two examples. The $\Gamma $ -method was claimed capable of simulating lifting surfaces with arbitrary camber, sweep and dihedral [23], which was later shown not to be the case for swept wings [30, 31]. Changes in the locus of the BVs and in the geometry of the TVs circumvented the convergence issues, but these changes influence the final circulation distribution [30, 33]. Likewise, literature showed good agreement of the $\alpha $ -method with experimental data including low aspect-ratio (AR) planforms [28], but the solutions were sensible to discretisation, and planform-dependent upper bounds for grid refinement were observed [28]. This issue was addressed by adapting the HSVs configuration [35], and preliminary verification studies showed grid independence of the solution, but at the cost of restricting the method to moderate- and high-AR planforms. The remainder of this paper not only formally confirms previous results but also extends them to more general conclusions by means of standard V&V procedures.

3.1 Code and solution verification

Procedures for code and solution verification and for error and uncertainty estimation are well reported in several references, and the approach taken follows the ASME Standard for verification and validation in CFD [15] and the work of Eça & Hoekstra [13]. Convergence was assessed by ${C_L}$ , with the numerical uncertainty ${U_N} \equiv {U_r} + {U_i} + {U_h}$ , made of round-off ${U_r}$ , iterative ${U_i}$ , and discretisation ${U_h}$ uncertainties, assumed to be dominated by the discretisation uncertainty ${U_h}$ ; such assumption is reasonable as calculations were carried using double-precision arithmetic, ensuring round-off error to be about ${10^{ - 16}}$ while both iterative and discretisation errors were at most in the order of ${10^{ - 10}}$ , significantly smaller than the orders of ${C_L}$ ; on the other hand, when convergence issues happened ${U_h}$ was much higher than the other sources.

The methods were tested for planforms whose analytic solutions derived from the classic lifting-line theory, so specific aspects of the implementations could be assessed. For elliptically loaded wings, Prandtl’s equation reduces to [36]:

(16) \begin{align}\Gamma (y) = \Gamma (0){\left[ {1 - {{\left( {\frac{{2y}}{b}} \right)}^2}} \right]^{1/2}} = \frac{1}{2}\frac{{\partial {C_l}}}{{\partial \alpha }}{|_y}c(y)\left\{ {{V_\infty }\left[ {\alpha (y) + \theta (y)} \right] - \frac{{\Gamma (0)}}{{2b}}} \right\}\end{align}

in which y refers to the wing spanwise direction and $\theta (y)$ spanwise twist and/or zero-lift angle. Equation (16) reveals many ways to geometrically generate elliptic lift distributions, so three planforms were generated and their characteristics were summarised on Table 2: (i) elliptical planform refers to a spanwise elliptical $c(y)$ distribution to test the methods capabilities in the presence of variable local incidence velocity and effective AoA; (ii) elliptical slope refers to a spanwise elliptical $\dfrac{{\partial {C_l}}}{{\partial \alpha }}(y)$ distribution to assess the inclusion of aerofoil data that deviate from the ideal $2\pi \;{\textrm{ra}}{{\textrm{d}}^{ - 1}}$ ; and (iii) elliptical twist refers to a $\theta (y)$ distribution to test the methods capabilities for nonplanar wing geometries. Two additional configurations with no analytic solutions were also included: (iv) sweptback refers to a 45-degree sweptback planform and (v) dihedral refers to a 4-degree dihedral one. All these geometric properties are important not only to aerodynamic wing design, but also to the extension of LL methods to rotating lifting-surfaces [6].

Table 2. Wings used for verification

The discretisation error ${\epsilon _{{C_L}}}$ was first estimated through a five-step procedure for the application of the grid convergence index, based on a power-series representation, or Richardson extrapolation method (RE) [15]:

(17) \begin{align}{\epsilon _{{C_L}}} \simeq {\delta _{RE}} = {C_L}({h_j}) - {C_{Lext}} = Ah_j^p + H.O.T,\quad {h_j} = {{\sum\nolimits_{i = 1}^{{N_j}} {\delta {l_i}} } \over {{N_j}}}\end{align}

with ${\delta _{RE}}$ the RE estimate, A a constant, p the observed order of grid convergence, ${h_j}$ a typical grid size, and ${C_{Lext}} = \mathop {\lim }\nolimits_{{h_j} \to 0} \;{C_L}\!\left( {{h_j}} \right)$ . Equation (17) assumes that the solutions are in the asymptotic range to ensure high-order terms (H.O.T.) can be neglected and that the grids could be represented by the single typical grid size ${h_j}$ , which requires an almost constant grid refinement ratio $r{r_j} \equiv \dfrac{{{h_{j + 1}}}}{{{h_j}}}$ and unaffected grid properties; while the former is virtually impossible to be determined [13, 15], the latter is easily attainable for LL methods. Finally, cosine clustering discretisation was preferred, as convergence is expected to happen faster than equidistant clustering for the same family of grids [17, 23].

The procedure was applied on several grid triplets, and if the attempt was not successful or if significantly discrepant results were found for the successive triples, i.e. significantly different p that arise from small data perturbations, then non-weighted (LSN) and weighted (LSW) least square approaches were applied at two extra sets [13], one from grids I to IV, and the other from I to V. The best approach was determined based on the least square that yielded the smallest standard deviation $\sigma $ , given all data were classified as monotonically convergent $\left( {p \gt 0} \right)$ [13]; when $p \gt 2.1$ or $p \lt 0.5$ , however, ${\delta _{RE}}$ was dropped in favor of more appropriate estimators, ${\delta _1}$ , ${\delta _2}$ , or ${\delta _{12}}$ , that were again evaluated by LSN and LSW and the chosen estimator based on the smallest $\sigma $ [13]:

(18) \begin{align}{\epsilon _{{C_L}}} \simeq {\delta _1} = {A_1}{h_j}\end{align}

(19) \begin{align}{\epsilon _{{C_L}}} \simeq {\delta _2} = {A_2}h_j^2\end{align}

(20) \begin{align}{\epsilon _{{C_L}}} \simeq {\delta _{12}} = {A_1}{h_j} + {A_2}h_j^2\end{align}

Note that the ${A_s}$ in the expressions (18) to (20) are, in general, different. The same procedure was applied to estimate the uncertainty associated with ${C_D}$ that will be used later in the ${C_L} \times {C_D}$ plots, although not reported in this paper. With code and solution verification results established, analytic ${C_L}$ from the elliptically loaded planforms were compared to results from both methods by varying the AoA while keeping the geometry fixed and vice-versa. Results are presented next.

3.1.1 Convergence analysis

For a fixed AoA of ${4^ \circ }$ , a set of 14 grids was simulated with ${N_{max}} = 7{,}168$ (grid ‘I’), ${N_{min}} = 80$ (grid ‘XIV’), and $r{r_j} \approx \sqrt 2 $ . Three subsets of three adjacent grids were used for estimation of $\epsilon_{C_{L}}$ through RE; however, as this procedure did not yield adequate results for almost all cases, the least square approach was preferred.

Figure 4 presents $\left( {{C_L}(h) - {C_{Lext}}} \right) \times \dfrac{h}{{{h_{min}}}}$ (dots) and the selected $ \delta \times \dfrac{h}{{{h_{min}}}}$ (lines) for all planforms; while for the elliptically loaded wings, both methods perform equally well, for the sweptback and dihedral wings, the $\alpha $ -method significantly outperforms the $\Gamma $ -method, whose plots indicate convergence issues.

The observed p and ${U_h}$ , relative to ${C_{Lext}}$ , are summarised in Table 3. For the $\alpha $ -method, $p \approx 2$ for almost all wings and even when more appropriate estimators are used, those are of quadratic order; the maximum ${U_h}$ is not higher than ${10^{ - 4}}\% $ . For the $\Gamma $ -method, in the case of the elliptically loaded wings most p and ${U_h}$ are similar to the $\alpha $ -method, with the exception of p for the elliptical planform wing, whose best error estimator was of first order; for the sweptback and dihedral wings, the method presents convergence issues [15], which can be observed by the uncertainties ranging from ${10^{ + 1}}\% $ to from ${10^{ + 3}}\% $ . Therefore, these results formally extend what has been initially reported in the literature [31, 32]: while $\Gamma $ -formulations present convergence issues not only to planforms with sweep angles, but non-straight $\dfrac{c}{4}$ lines in general, $\alpha $ -formulations are naturally more advantageous for solving more complex geometry configurations.

Table 3. Results for grid convergence. For $p \lt 0.5$ and $p \gt 2.1$ , ${\delta _{Re}}$ was substituted for appropriate estimators - Finest grids $\left( {{N_{max}} = 7{,}168} \right)$

Figure 4. Convergence rates for the $\alpha $ - and $\Gamma $ -methods.

LL methods are designed to be computationally fast, and although the literature has suggested that grid convergence is obtained for $N \geq 80$ [23, 37], to the knowledge of the authors no uncertainty quantification has been reported. Therefore, the same analysis is performed for grids of practical purposes ( ${N_{max}} = 224$ ), whose results are presented in Table 4; for the elliptically loaded wings both methods again returned p within acceptable ranges [13], and although ${U_h}$ increased by up to 1,000 times in a few cases, they are still negligible with respect to ${C_L}$ and other sources of uncertainty. For the sweptback and dihedral wings, the results are almost the same as in the case of the most refined grids, with the associated uncertainties still large for the $\Gamma $ -method. Therefore, $N = 224$ presents a good compromise between accuracy and computation time and so is used for the remaining of this paper.

Table 4. Results for grid convergence. For $p \lt 0.5$ and $p \gt 2.1$ , ${\delta _{Re}}$ was substituted for appropriate estimators - practical purposes grids $\left( {{N_{max}} = 224} \right)$

Finally, it should be pointed out that the same procedure was applied to lower and higher AoAs, and the results were in the same orders of magnitude for all combinations of wings and methods. Therefore, Tables 3 and 4 accurately reflect the orders of magnitude of the uncertainties for the ranges of AoAs simulated in the validation procedure.

3.1.2 Comparison with results from Prandtl’s classic lifting-line theory

To measure how much the methods deviate from the classic theory, the difference $\Delta {C_L} \equiv {C_L} - {C_{L,CLL}}$ between the results from numerical simulations and the analytic solution for elliptically loaded wings, ${C_{L,CLL}}$ , is assessed; ${C_{L,CLL}}$ can be written as [17, 36]:

(21) \begin{align}{C_{L,CLL}} = \pi AR\frac{1}{{1 + \frac{{4b}}{{\frac{{\partial {C_l}}}{{\partial \alpha }}{\big|_{y = 0}}c(0)}}}}\left[ {\alpha (0) + \theta (0)} \right]\end{align}

with AR the wing aspect ratio and b the wing span. Figure 5 shows $\Delta {C_L}$ versus $\alpha $ for fixed geometries, and versus AR, $\theta $ , and $\dfrac{{\partial {C_l}}}{{\partial \alpha }}$ for fixed $\alpha $ . In most cases, the $\alpha $ -method underestimated the magnitude of ${C_L}$ while the $\Gamma $ -method yielded the closest results to Prandtl’s theory, meaning the $\Gamma $ -method is expected to overshoot experimental data. It remains to show that this is the case, which is one of the purposes of validation.

Figure 5. Difference between numerical and theoretical ${C_L}$ versus $\alpha $ and some wing-design parameters for the $\alpha $ - and $\Gamma $ -methods.

3.2 Validation

Both $\alpha $ - and $\Gamma $ -methods are validated against experimental data and compared to numerical results reported in the literature; whenever possible, results followed these guidelines:

1. 1. Aerofoil data were the same for all methods, as they significantly impact the overall ${C_L}$ and ${C_D}$ . They generally came from the reference describing the numerical method(s) under comparison.

2. 2. Uncertainties were combined through a standard uncertainty propagation so they would only be at the y-axis.

3. 3. Numerical uncertainties considered all possible sources, such as grid, experimental inputs [15] (i.e., Re, $\alpha $ ) and aerofoil data. Whenever available, experimental uncertainties were also presented.

4. 4. Cosine clustering was again used.

5. 5. For wings with sweep or dihedral, results from the $\Gamma $ -method were still presented, but with the uncertainties omitted for clarity. In these cases, the results should be rather assessed qualitatively.

3.2.1 Almost-elliptical planform wing

Figures 6 and 7 present the results for the first wing, which has an elliptical planform with a rectangular inboard and NACA 0012 aerofoil sections. Experiments [38] were performed at a free-stream Reynolds number $R{e_\infty } \approx 1.35 \times {10^6}$ with respect to ${c_0}$ . Along with the $\alpha $ - and $\Gamma $ -methods, numerical results from an $\alpha $ -formulation (W-G) of Wickenheiser and Garcia [39] are also presented; but as the circulation distribution is cast as a sine series, the nonlinear scheme differs from the $\alpha $ -method as ${\alpha _{eff}}$ is directly updated. The 2-D aerofoil data for all methods also comes from Wickenheiser and Garcia, which have been generated with JavaFoil using NACA standard surface finish and the Eppler standard transition model [39].

Figure 6. (left) ${C_L} \times \alpha $ and (right) ${C_D} \times \alpha $ . Almost-elliptical planform wing.

Figure 7. ${C_L} \times {C_D}$ (left) without and (right) with ${C_D}$ shift. Almost-elliptical planform wing.

The ${C_L} \times \alpha $ plot on Fig. 6 shows that all numerical methods qualitatively agree with experiments up to stall, with the $\alpha $ -method performing suitably better at higher AoAs. From the ${C_D} \times \alpha $ plot, all methods overestimate the drag coefficient with respect to experiments by almost the same amount $\Delta {C_D}$ , which could have been addressed with more adequate source of aerofoil data [31]. Additionally, in comparison to the $\alpha $ -method, the $\Gamma $ -method slightly underpredicts ${C_D}$ , specially at ${5^ \circ } \le \alpha \le {10^ \circ }$ .

In Fig. 7, the left plot presents ${C_L} \times {C_D}$ with the original data, while the right plot presents ${C_L} \times {C_D}$ with the numerical data corrected by $\Delta {C_D}$ so as to coincide with the experimental results; with this correction, it can be observed that the $\Gamma $ -method tends to overpredict $\dfrac{L}{D}$ , as expected from the previous discussion, while the W-G and $\alpha $ -method present similar $\dfrac{L}{D}$ values, close to the experimental data. As pointed out in the ${C_L} \times \alpha $ and ${C_D} \times \alpha $ plots, even though the differences in the W-G and $\alpha $ -methods are subtle, a similar ${C_L} \times {C_D}$ for these two methods is a consequence of the overprediction of both ${C_L}$ and ${C_D}$ for a given $\alpha $ in the case of the W-G method.

3.2.2 Crescent wing

The second wing has a similar planform but with a variable sweep angle distribution, and it has been experimented at the same conditions [38]. Numerical results from the W-G method are again shown for comparison, with the same source of 2-D data [39]. The results are illustrated in Fig. 8.

Figure 8. (left) ${C_L} \times \alpha $ and ${C_D} \times \alpha $ (right). Crescent wing.

The ${C_L} \times \alpha $ plot shows that the overall agreement is again adequate, with all methods slightly overshooting the experimental data and both $\alpha $ - and $\Gamma $ -methods performing slightly better. However, it is the presence of sweep that made the $\Gamma $ -method perform similar to the $\alpha $ -, as well as to fail at higher AoAs, as previously indicated by the verification procedure. Finally, no method adequately predicted stall, but the W-G seemed to predict the angle of occurrence.

For the ${C_L} \times {C_D}$ plot, the same right shift exists, but only the $\alpha $ -method kept a constant difference for most of the ${C_L}$ range; so, as in the case of the almost-elliptical wing, in absence of such shift, W-G would overpredict $\frac{L}{D} $ , the $\Gamma $ -method would underpredict it and the $\alpha $ -method would yield the closest results to experiments.

3.2.3 Rectangular wing

Figure 9 shows the results for a NACA 0012 rectangular wing tested at $R{e_\infty } \approx 2.11 \times {10^6}$ [40]. Numerical results from a mixed-formulation (WNLL) [22] and another $\Gamma $ -formulation (PNLL) [24] are shown for comparison. The aerofoil data used is from Owens [22], which assumes that ${C_d} = 0$ , so a constant wing viscous drag contribution ${C_{D0}} = 0.009364$ was added to all $\alpha $ range.

Figure 9. (left) ${C_L} \times \alpha $ and (right) ${C_L} \times {C_D}$ . Rectangular wing.

The ${C_L} \times \alpha $ plot shows that, for most of the AoAs, the $\alpha $ -method and WNLL agree well to each other, and so the $\Gamma $ -method and PNLL; the $\alpha $ -method and WNLL agree better to the experimental data than the $\Gamma $ -formulations, which present the ${C_L}$ overshoot previously indicated in the verification procedure. Additionally, for $\alpha \geq 12^{\circ}$ the $\Gamma $ -method presented convergence issues. Finally, the stall angle was correctly predicted only by the PNLL and WNLL.

The ${C_L} \times {C_D}$ curve shows that the $\Gamma $ -formulations again overpredict $\dfrac{L}{D}$ , while the best agreement happens for the WNLL, followed by the $\alpha $ -method. The differences between those two are nonetheless unexpected, as ${C_{Di}}$ depends on ${C_L}$ , which are similar for both, and since no different treatment for ${C_{Di}}$ was reported in the implementation of WNLL [22], both formulations should yield similar curves.

3.2.4 45-deg sweptback wing

Results for a RAE-10112 45-deg sweptback wing are shown in Fig. 10, with experiments conducted at $R{e_\infty } \approx 1.68 \times {10^6}$ [41] and numerical simulations from the WNLL [22] and an adaptation of the $\Gamma $ -method (G-H) [33] that corrects it to enable the simulation of sweptback wings. The aerofoil data was pre-generated by the open source code XFOIL [42] with its standard viscous model activated, while for the G-H method, a constant $\dfrac{{\partial {C_l}}}{{\partial \alpha }} = 5.935\;Ra{d^{ - 1}}$ was assumed, while for the WNLL nothing has been reported.

Figure 10. (left) ${C_L} \times \alpha $ and (right) ${C_L} \times {C_D}$ . 45-deg sweptback wing.

From the ${C_L} \times \alpha $ curve, the differences between the $\Gamma $ -method and its improved version (G-H) are readily observed; however, even with the G-H method addressing the convergence issues, it still does not address the lift overprediction of $\Gamma $ -formulations, and again both the $\alpha $ -method and WNLL best match experimental data. The ${C_L} \times {C_D}$ plot corroborates the G-H $\dfrac{L}{D}$ overprediction while showing that the $\alpha $ -method best agrees with experimental data. For the WNLL, no results for ${C_D}$ were reported [22].

Figure 11 shows the wing section lift distribution ${C_{l,ws}}$ at $\alpha = 4.2\deg $ , normalised by ${C_L}$ . As observed by Reid and Hunsaker [32], the $\Gamma $ -method does not accurately predict ${C_{l,ws}}$ , and the underpredicting lift that starts at root and propagates towards the tips is a direct consequence of the dependence of ${\bf{V}}$ on the grid resolution, as shown in the Verification section. In its improved version, the G-H method qualitatively agrees with the experimental data as well as the $\alpha $ -method.

Figure 11. $\dfrac{{{C_{l,ws}}}}{{{C_L}}}$ distribution for $\alpha ={4.2^ \circ }$ . 45-deg sweptback wing.

3.2.5 Twisted wing with taper

The fifth wing has a linearly varying twist whose root and tip angles are ${0^ \circ }$ and $ - {3.50^ \circ }$ and the respective aerofoils are NACA 4,420 and NACA 4,412 with lofted sections in between. It also has a taper ratio $c(y=b)/c(y=0) = 0.4$ and a tip parabolic rounding [20], but the $\dfrac{c}{4}$ line is still straight. Experiments were conducted at $R{e_\infty } \approx 3.49 \times {10^6}$ [20, 43] (wing ‘2.5-10-44,20’), which have also provided the source for aerofoil data [20]. Figure 12 shows the results, which include the numerical simulations from the W-G $\alpha $ -formulation [39].

Figure 12. (left) ${C_L} \times \alpha $ and (right) ${C_L} \times {C_D}$ . Twisted wing with 0.4 taper ratio.

Both ${C_L} \times \alpha $ and ${C_L} \times {C_D}$ show that, up to stall, all methods compare well to experimental data; while the polar plots look quite similar, the W-G [39] performed slightly better in the ${C_L} \times \alpha $ curve for higher AoAs, which could be a consequence of how the aerofoil data in the mid-sections was calculated [31] (for both $\alpha $ - and $\Gamma $ -methods it is done through linear interpolation, while for the W-G it is not reported), but further analysis would be necessary. Finally, the $\Gamma $ -method failed to converge at higher AoAs.

3.2.6 3-deg dihedral wing with taper

The last wing has a 3-deg dihedral, $c(y=b)/c(y=0) = 0.4$ , tip parabolic rounding, and NACA 65,210 sections throughout, whose data source comes from Abbott & Von Doenhoff [22, 44, 45]. Experiments were performed at $R{e_\infty } \approx 4.40 \times {10^6}$ [45] and numerical simulations are again from the WNLL [22]. Figure 13 shows the results.

Figure 13. (left) ${C_L} \times \alpha $ and (right) ${C_L} \times {C_D}$ . 3-deg dihedral wing with 0.4 taper ratio.

Both curves show that all numerical results compare well to experimental data, but the presence of dihedral prevented the $\Gamma $ -method convergence for $\alpha \geq 8^{\circ}$ , as expected from the verification procedure. Additionally, the $\alpha $ -method and the WNLL [22] present almost indistinguishable curves, which corroborates the discussion about the unexpected differences in the ${C_L} \times {C_D}$ plots observed for the straight wing case, Fig. 9.

4.0 Conclusion

This paper presented rigorous verification and validation procedures for two main lifting-line formulations that exist in the literature, named $\alpha $ - and $\Gamma $ -formulations. Verification, Section 3.1.1, showed that the $\alpha $ -method converges well for all geometries with the highest grid uncertainty in the order of ${10^{ - 3}}\% $ and most convergence rates close to quadratic, while the $\Gamma $ -method presented significantly larger uncertainties (in the order of ${10^{ + 3}}\% $ ) and low convergence rates for wings with dihedral and sweep, clearly pointing out convergence issues. Further comparison to analytic results from the classic formulation, Section 3.1.2, revealed that the $\Gamma $ -method agrees most with them, whereas the $\alpha $ -method typically yields lower absolute values, revealing a tendency of the $\Gamma $ -method to overpredict ${C_L}$ when compared to experiments. Validation, Section 3.2, corroborated the $\Gamma $ -method convergence issues observed for wings with nonstraight $\dfrac{c}{4}$ lines and, even with modifications to circumvent them, its tendency to overpredict ${C_L}$ . On the other hand, it showed that $\alpha $ -method is the one that best agreed with experimental data for most of the cases and, consequently, its advantages over the other methods presented.

As a final remark, in addition to the wake geometric construction and easy adaptation, the $\alpha $ -method capability of simulating wings of general geometry, confirmed by the V&V procedure, makes it potentially superior in the extension of modern lifting-line methods to rotating lifting surfaces with nonstraight quarter-chord lines.