Published online by Cambridge University Press: 01 August 2014
Spatial models of party competition constitute a recent and incrementally developing literature which seeks to explore the relationships between citizens' decisions and candidates' strategies. Despite the mathematical and deductive rigor of this approach, it is only now that political scientists can begin to see the incorporation of those considerations which less formal analyses identify as salient, and perhaps crucial, features of election contests.
One such consideration concerns the candidates' objectives. Specifically, spatial analysis often confuses the distinction between candidates who maximize votes and candidates who maximize plurality. Downs and Garvey, for example, assume explicitly that candidates maximize votes, though plurality maximization is clearly the assumption which Garvey actually employs, while Downs frequently assumes that vote maximization, plurality maximization, and the goal of winning are equivalent. Downs, nevertheless, attempts to disentangle these objectives, observing that plurality maximization is the appropriate objective for candidates in a single-member district, while vote maximization is appropriate in proportional representation systems with many parties. All subsequent spatial analysis research, however, assumes either implicitly or explicitly that candidates maximize plurality. If Downs is correct, therefore, this research may not be relevant for a general understanding of electoral competition in diverse constitutional or historical circumstances. The question then is whether those strategies that maximize votes differ from those strategies that maximize plurality.
This research was supported by a grant from Resources for the Future, Inc., to Carnegie-Mellon University, and a National Science Foundation Grant to the University of Rochester. We wish to thank a number of colleagues who have helped contribute improvements to our argument, especially Peter H. Aranson, University of Rochester and Howard Rosenthal, Carnegie-Mellon University.
* This research was supported by a grant from Resources for the Future, Inc., to Carnegie-Mellon University, and a National Science Foundation Grant to the University of Rochester. We wish to thank a number of colleagues who have helped contribute improvements to our argument, especially Peter H. Aranson, University of Rochester and Howard Rosenthal, Carnegie-Mellon University.
1 Downs, Anthony, An Economic Theory of Democracy, (New York: Harper and Row, 1957)Google Scholar. The recent theoretical developments based on Downs's work include: Davis, Otto A. and Hinich, Melvin J., “A Mathematical Model of Policy Formation in a Democratic Society,” in Mathematical Applications in Political Science II, Bernd, J. L., ed., (Dallas: SMU press, 1966)Google Scholar; “Some Results Related to a Mathematical Model of Policy Formation in a Democratic Society,” in Mathematical Applications in Political Science III, Bernd, J. L., ed., (Charlottesville: University Press of Virginia, 1967)Google Scholar; “On the Power and Importance of the Mean Preference in a Mathematical Model of Democratic Choice,” Public Choice, 5, (1969)Google Scholar; “Some Extensions to a Mathematical Model of Democratic Choice,” forthcoming in Social Choice, Lieberman, B. (ed.), (New York: Gordon and Breach)Google Scholar; with Ordeshook, Peter C., “An Expository Development of a Mathematical Model of the Electoral Process,” This Review, (June, 1970)Google Scholar; Hinich, Melvin J. and Ordeshook, Peter C. “Abstentions and Equilibrium in the Electoral Process,” Public Choice 7, (1969)Google Scholar; “Social Welfare and Electoral Competition in Democratic Societies,” (School of Urban and Public Affairs, Carnegie-Mellon University, 1969)Google Scholar; Ordeshook, Peter C., “Extensions to a Mathematical Model of the Electoral Process and Implications for the Theory of Responsible Parties,” Midwest Journal of Political Science (February 1970)CrossRefGoogle Scholar; Theory of the Electoral Proce (unpublished PhD Dissertation, University of Rochester); with Aranson, Peter H., “Spatial Strategies in Sequential Electrons” in Niemi, R. and Weisberg, H., Probability Models in Politic Science (forthcoming)Google Scholar; Tullock, Gordon, Toward a Mathematics of Politics, (Ann Arbor: University of Michigan Press, 1968)Google Scholar; Chapman, David E., “Models of the Working of a Two-Party Electoral System,” Papers on Non-Market Decision Making III, (Fall 1967)Google Scholar and Public Choice, 5, (1969)Google Scholar; Garvey, Gerald, “The Theory of Party Equilibrium,” this Review, LX, (1966)Google Scholar.
2 Downs, ibid, confuses vote maximization and plurality maximization in asserting that “each party seeks to receive more votes than any other;” thus the “self-interest axiom [leads] to the vote maximizing government (p. 31),” and that all the actions of the party “are aimed at maximizing votes (p. 35).” Similarly, Garvey, ibid, states that “parties shift their platforms whenever such a shift will increase chances to gain a majority. Thus, each party constantly ‘mobilizes’ to represent the views of a larger portion of society (p. 30).” And while Tullock, ibid, initially identifies the comparative evaluation of a party's vote (which is implicit in the measure of plurality) as the party's objective by stating that “the party or candidate who receives the most votes will be given control” (p. 51), he apparently assumes throughout his analysis that this implies that candidates maximize votes. Perhaps the most careful investigation of the candidates' objectives is presented by Riker, William H., who offers what appears to be an additional possibility in The Theory of Political Coalitions (New Haven: Yale 1962)Google Scholar. Specifically, Riker argues that rational politicians do not maximize votes (or, conceivably, plurality), but that they seek minimal winning coalitions. Observe, however, that if two candidates compete the election is a zero sum game, in which case the maximization of plurality and the formation of minimal winning coalitions lead to identical results—the selection of minimax strategies. Riker's criterion yields the adoption of different strategies only if the position of one candidate is fixed, so that his opponent adjusts his position to suit his objectives with the opponent's strategy a fixed parameter of his calculus.
3 The model we seek to extend is presented in the references to Davis, Hinich. and Ordeshook, op. cit.
4 Ibid.
5 By symmetry we mean that if the mean of f(x) is normalized to zero, f(x)=f(−x). This assumption is referred to as radial symmetry.
6 Clearly, alternative assumptions concerning the relationship of turnout to the candidates strategies are possible. For example, in Ordeshook, “Some Extensions …,” op. cit., abstention from indifference is analyzed. As yet, however, we have not incorporated this alternative assumption into our analysis of vote maximization.
7 Additionally, we assume that the expected value of ϵ is zero, and that it possesses a continuously differentiable density function defined in the interval (− ∞, ∞). Also, we assume that ϵ is distributed independently of U(x, θ).
8 This assumption does not imply an interpersonal comparison of utility, but simply that if the preference vectors of two citizens are equidistant from their preferred candidate(s), then the benefits and costs of voting, as well as the density of ϵ, stand in the same relationship to each other for both citizens.
9 We assume, moreover, that
10 Recall that a citizen's loss, Φ(x−θ), is a monotonic function of the metric ‖x−θ‖A, where A is a positive definite n×n matrix. If this loss matrix is identical for all citizens (Assumption 6), there exists a linear transformation of the dimensions such that A becomes the identity matrix I. Thus, with no loss of generality we can assume that Φ(x−θ)=Φ(‖x−θ‖), where x and θ are now measured in the transformed space. And since ‖x−θ‖ is constant on circles, Φ(x−θ) is constant on circles. Similarly, this transformation can also be designed so that, without any loss of generality, the axes of f(x) correspond to the axes of our coordinate space.
11 An interpretation of this special case renders analysis with it less objectionable. Briefly, if the analysis is multidimensional, and if all dimensions of taste are assumed to be identified and measured then there may be little randomness in decision-making.
12 This assumes that the candidate's plurality is not minimized if δ P(θ, ψ)/δθ = 0. By inspection however, we can generally eliminate such possibilities.
13 To differentiate V(θ, ψ) with respect to θ we apply Leibnitz's rule (see Hildebrand, Francis P., Advanced Calculus for Applications (Englewood Cliffs: Prentice Hall, 1963), p. 360 Google Scholar, or any textbook of advanced calculus) and get,
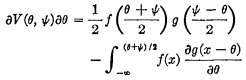
Integrating this expression by parts yields equation (7).
14 “Abstentions and Equilibrium …” op. cit.
15 The rectangular abstention function equals 0 for all x in the intervals (− ∞, θ −δ), and (θ+ δ, ∞) and equals 1 otherwise. Hence, equation (7) becomes,

Observe now that whenever g((ψ−θ)/2)=0, δV(θ, ψ)/δθ is positive. Hence candidate 1 should shift towards candidate 2 at least until g((ψ−θ)/2)= 1. This occurs whenever the two abstention functions butt against each other or overlap. We can restrict ourselves then to strategies such that g((ψ−θ)/2)= 1, in which case we get equation (9). Note, however, that if f(x) is a uniform density, f'(x) = 0 in the relevant range of integration. This means that either the rate of change of V(θ, ψ) with respect to θ is zero or that it is negative. It is zero if the abstention functions do not butt, it is negative if they overlap. Thus, if f(x) is a uniform density, the candidates do not converge so closely that the abstention functions of citizens preferring them overlap.
16 Additionally, with the rectangular abstention function we can easily illustrate the proof that for n = 1, only one strategy pair is an equilibrium pair. First, assume that θ≠ −ψ, and that δV(ψ,θ)/δψ=0. Thus,
or, equivalently,
Now consider δV(θ, ψ)/δθ, which we know equals ½f((θ+ψ)/2)−f(θ − δ). Thus, from the condition that δV(ψ,θ)/δψ=0, δV(θ, ψ)/δθ=f(ψ+δ)−f(θ−δ). But, f(x) is symmetric about 0, and θ≠−ψ, so that f(θ−δ)≠f(ψ+δ). Thus, δV(θ,ψ)/δθ≠0, which is to say that δV(θ,ψ)/δθ and δV(ψ, θ)/δψ cannot equal 0 simultaneously for θ ≠ − ψ. This proves, for rectangular abstention function, that only a strategy pair satisfying θ = −ψ≤0 is an equilibrium pair. To prove that only one such strategy pair satisfies this condition for a given δ and f(x), we set ψ = − θ and get,
Obviously, this function equals zero for only one θ since f(0)/2 is a constant and f(θ − δ) is monotonically increasing with θ for all θ≤0.
17 If θ is less than δ − x*, then f(θ−δ)<f(−x*)= f(0)/2, in which case δV(θ, ψ)/δθ>0 from equ tion (11), and candidate 1 should shift towards the mean. Alternatively, if θ >δ − x*, δV(θ, ψ)/δθ<0 and candidate 1 should shift away from the mean.
18 Let δ>x*. Thus, since f(x) is unimodal and θ≤0, f(−x*)>f(θ−δ), in which case δV(θ, ψ)/δθ>0 for all θ≤0; the candidates converge to the mean. Now consider δ≤x*. From equation (11), the condition for a maximizing value of θ is f(0)/2=f(θ−δ)=f(−x*). If 2δ≥x*, an equilibrium is attained by selecting θ such that −θ= −x*+δ (this insures that f(θ−δ)=f(x*)=f(0)/2). Clearly, then, as δ diminishes from x* to x*/2, θ diminishes from 0 to −x*/2. Finally, if 2δ<x*, equation (11) cannot be satisfied without violating the condition that the two candidates' abstention functions at least butt against each other. Thus, an equilibrium is attained by setting −θ=δ (observe that for −θ<δ, δV(θ, ψ)/δθ>0, but for −θ>δ, this rate of change is negative). Thus, as δ diminishes from x*/2 to 0, θ increases from −x*/2 to 0.
19 For example, a continuously differentiable abstention function can yield the relationship between δ and the equilibrium value of θ illustrated in Figure 12.
20 The notion of a “uniform” variation in the cost of voting is defined rigorously in Hinich and Ordeshook, “Abstentions and Equilibrium…,” op. cit. Briefly, if two citizens are the same distance from their preferred candidates, they vote with equal probability; and a variation in the cost of voting is said to be uniform if they continue to vote with equal probability after such costs are altered (and if the abstention function g retains the mathematical properties we assume for it). For example, if g is the rectangular abstention function we can associate a δ with each person's function. We assume in our analysis that the same value for δ is associated with all citizens functions. Changing the cost of voting changes the magnitude of δ and a uniform variation in the cost of voting change δ equally for all citizens.
21 Ibid. We also demonstrate, however, that if f(x) is not symmetric and if the candidates maximize votes, the location of a dominant strategy is sensitive to variations in sensitivity.
22 Op. cit., p. 115, 126–127. Tullock, op. cit., p. 54–56, concludes for two issues, if all citizens vote, and if preferences are distributed uniformly over a rectangle or a circle, that three candidates do not converge. His illustration, however, assumes the consequence: Tullock's Figure XXXIX (p. 55) requires that candidates A and B have not adopted identical positions. If A and B are at the same point, however, then clearly candidate C should converge arbitrarily close to this point since this move maximizes both his plurality and his total vote. A careful scrutiny of this situation, nevertheless, yields some interesting observations. First, if all three candidates converge arbitrarily close to the mean, it is readily verified that such convergence is an equilibrium—no candidate has any incentive to shift unilaterally from the mean. Second, equilibria exist in which all three candidates adopt dissimilar positions symmetrically about the mean. In fact, there appear to be an infinity of equilibria triples—including convergence. This suggests that the final equilibrium triple is a function of initial conditions (e.g., the candidates' initial positions and whatever restrictions on strategies that exist) and their reaction paths. Clearly, then, multidimensional analysis of multiparty systems requires careful analysis, and this analysis undoubtedly will reveal many interesting and nonobvious conclusions. We are not prepared in this essay to conduct such an analysis, however, so we restrict our discussion to undimensional competition.
23 Throughout this section we also assume that if a citizen votes, he votes for his most preferred candidate. Casstevens, Thomas W. attempts to show that this assumption follows logically from the voter's decision theoretic calculus in “A Theorem About Voting.” this Review, LXII (March, 1968)Google Scholar. But Casstevens assumes that if a voter switches from candidate 1 to candidate 2, he does not affect the probability that candidate 3 wins—an assumption which does not follow logically from his structure (see Gerald H. Kramer, letter to the editor, this Review, LXII (September, 1968)). Note however, that we are assuming that the candidates maximize votes, in which case the behavioral proposition that citizens vote for a preferred candidate to increase a candidate's total vote is admissable. For a decision-theoretic analysis of a citizen's calculus in multiparty systems see McKelvey, Richard and Ordeshook, Peter C., “A General Theory of the Calculus of Voting,” (unpublished, University of Rochester, 1970 Google Scholar.)
24 Riker, William H., Ordeshook, Peter C., and Rai, Kul B., “A Theory of the Number of Political Parties” (unpublished, University of Rochester, 1970)Google Scholar.
25 The restriction that candidates cannot cross each other is suggested by Downs, op. cit., p. 123.
26 To see this assume that α and θ are fixed and let β form to the right of ψ. The rate of change in votes for ψ becomes,
Clearly, since f(x) is unimodal and θ is fixed at the mean with β>ψ>θ,
Thus, ψ converges to θ. It is readily shown that θ has no incentive now to shift to the left, so that with β assuming the old position of ψ the candidates are in equilibrium.
27 Davis, Hinich, and Ordeshook, op. cit.
28 “Majority Rule and the Representative System of Government,” in Cleavages, Ideologies and Party Systems: Contributions to Comparative Political Sociology, ed. by Allardt, E. and Littunen, Y. (Helsinki: Transactions of the Westermarch Society, 1964), p. 359, 376 Google Scholar.
Comments
No Comments have been published for this article.