No CrossRef data available.
Article contents
Lapse risk modeling in insurance: a Bayesian mixture approach
Published online by Cambridge University Press: 01 September 2023
Abstract
This paper focuses on modeling surrender time for policyholders in the context of life insurance. In this setup, a large lapse rate at the first months of a contract is often observed, with a decrease in this rate after some months. The modeling of the time to cancelation must account for this specific behavior. Another stylized fact is that policies which are not canceled in the study period are considered censored. To account for both censoring and heterogeneous lapse rates, this work assumes a Bayesian survival model with a mixture of regressions. The inference is based on data augmentation allowing for fast computations even for datasets of over millions of clients. Moreover, frequentist point estimation based on Expectation–Maximization algorithm is also presented. An illustrative example emulates a typical behavior for life insurance contracts, and a simulated study investigates the properties of the proposed model. A case study is considered and illustrates the flexibility of our proposed model allowing different specifications of mixture components. In particular, the observed censoring in the insurance context might be up to 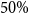 $50\%$ of the data, which is very unusual for survival models in other fields such as epidemiology. This aspect is exploited in our simulated study.
$50\%$ of the data, which is very unusual for survival models in other fields such as epidemiology. This aspect is exploited in our simulated study.
Information
- Type
- Original Research Paper
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Institute and Faculty of Actuaries

