Introduction
Glacier mass-balance data from the Antarctic Peninsula (AP) region are very scarce due to the logistical difficulty involved, the relatively large glacier areal extent and the extreme weather conditions throughout the year. Over the past century, climate warming of 3.5°C at the northern AP (Reference Morris, Vaughan, Domack, Burnett, Leventer, Conley, Kirby and BindschadlerMorris and Vaughan, 2003) has induced the retreat of land-terminating glaciers and ice-shelf disintegration on both sides of the AP (Reference Skvarca, Rott and NaglerSkvarca and others, 1995, Reference Skvarca, Rott and Nagler1999; Reference Rott, Skvarca and NaglerRott and others, 1996; Reference Skvarca, De Angelis, Domack, Burnett, Leventer, Conley, Kirby and BindschadlerSkvarca and De Angelis, 2003; Reference Braun, Humbert and MollBraun and others, 2009; Reference Cook and VaughanCook and Vaughan, 2010). Continuous monitoring of glacier mass balance is important for climate research due to the high sensitivity of polar regions to climate change (Reference WellerWeller, 1998). However, only a few glaciers on the AP and surrounding islands are monitored by field measurements (Reference Skvarca, De Angelis and ErmolinSkvarca and others, 2004; Reference Engel, Nývlt and LáskaEngel and others, 2012; Reference Navarro, Jonsell, Corcuera and Martín-EspañolNavarro and others, 2013; Reference MavlyudovMavlyudov, 2014).
It is generally assumed that mass-balance measurements can be reliably performed in the field using the glaciological method (Reference Østrem and BrugmanØstrem and Brugman, 1991). In order to reduce methodological uncertainties, it is recommended that the mass balance obtained by the glaciological method be calibrated and compared with the long-term geodetic volume change (Reference Zemp, Hoelzle and HaeberliZemp and others, 2009; Reference PaulPaul and others, 2013).
In this work, we present cumulative annual mass balances of Glaciar Bahía del Diablo, Vega Island, AP, for a period of ten hydrological years (Southern Hemisphere; as defined by the World Glacier Monitoring Service (WGMS) and Reference CogleyCogley and others (2011)) from 2002 to 2011. We also present geodetic mass change for the same period, determined from two glacier surface elevation models obtained by field kinematic GPS measurements in 2000/01 and 2011. The two results are compared in order to validate a mass-balance series reported to the WGMS database.
Study Area
Glaciar Bahía del Diablo is located on the northern slope of Vega Island, northeastern AP (63°49′ S, 57°26′ W; Fig. 1). The glacier is polythermal, with its snout overriding an ice-cored thrust moraine on a periglacial plain of continuous permafrost, with a mean equilibrium-line altitude (ELA) of ~400 m a.s.l. (Reference Skvarca, De Angelis and ErmolinSkvarca and others, 2004), and with an area of 12.9 km2 (recently reassessed by field measurements). Glaciar Bahía del Diablo is one of the land-terminating glaciers in the AP region. This is a very important feature since the mass balance of land-terminating glaciers is more directly related to local climate than is that of calving glaciers. Mass-balance measurements on Glaciar Bahía del Diablo started in the 1998/99 austral summer (Reference Skvarca, De Angelis and ErmolinSkvarca and others, 2004). Glaciological field surveys are carried out each summer, and consist of stake measurements, pit digging for snow density measurements, and stake network maintenance.

Fig. 1. (a) Location of Vega Island and (b) map of Glaciar Bahía del Diablo showing the glacier boundary and surface elevation contours (m a.s.l.). BASE indicates the location of the GPS base station, N indicates nunatak area, squares show snow-pit sites and the dots indicate the stake network. Dotted lines represent the snow-probing profiles. Area excluded from DEM analysis near the nunatak is indicated. Background satellite image from SPIRIT (SPOT 5 stereoscopic survey of Polar Ice: Reference Images and Topographies during the fourth International Polar Year (2007–09)) on 7 January 2006.
An average surface lowering of 12.6 m from 1985 to 1998, which was detected in the 1998/99 summer field campaign, led to the initiation of ablation/accumulation measurements over the whole glacier area (Reference Skvarca, De Angelis and ErmolinSkvarca and others, 2004). Since 1999, snow density and thickness have been determined on annual field campaigns by digging snow pits, and snow depth measurements are performed at several locations in the accumulation area. The logistical support of the nearby Marambio station, 60 km southeast of Glaciar Bahía del Diablo, allows only one visit per year during the austral summer. Annual glacier mass balance is obtained for each year from the field data and the results are reported in the Glacier Mass Balance Bulletin (Reference ZempWGMS, 2013).
Data and Methods
Annual mass balance was determined by applying the glaciological method with dates fixed due to logistical constraints (Reference Mayo, Meier and TangbornMayo and others, 1972). Each February, field campaigns were carried out to measure the stake network in order to determine annual ablation/accumulation at each point. The network consists of 20–24 stakes, with a density of ~2 stakes km–2 (Fig. 1b). In the accumulation area, snow thickness was measured along the stakes using a snow probe, and snow pits were dug at five locations (Fig. 1b) in order to obtain the mean snow density from stratigraphy analysis. The mass balance derived at each stake and probe site was then integrated by linear interpolation over the whole glacier area to obtain annual balance contours (m w.e.). The total annual mass balance was calculated from the mass-balance maps by means of PCI Geomatics software.
Kinematic GPS surveys were carried out in summer 1999/2000 over the accumulation area, in summer 2000/01 over the ablation area and in summer 2010/11 over the entire glacier area (Fig. 2). The same single-frequency GPS system (rover: Trimble® Pro XL, 8-channel; base: Trimble® 4600LS, 12-channel) was used during all three surveys. The base station was installed during each field campaign at the same benchmark near the camp, which is <9 km from all survey points (Fig. 1b). A rover antenna was mounted on a snowmobile to survey snow areas and on a backpack to survey ice areas by walking. The logging interval was 1 s for all surveys in a kinematic mode. Data for the three years were processed using Trimble Pathfinder Office software with Centimeter Processor enhancing capability, providing both horizontal and vertical precisions in the order of 0.1 m (Reference Skvarca, De Angelis and ErmolinSkvarca and others, 2004). Data acquired during the three field campaigns were integrated and two digital elevation models (DEMs) were constructed, one for 2000/01 and the other for 2011. DEMs were derived from the GPS data at the survey points by kriging interpolation with a linear variogram using a 10 m × 10 m grid.

Fig. 2. GPS survey tracks performed (a) in 2000 (black) and 2001 (grey) and (b) in 2011. Dots indicate the stake network.
We established that the surface elevation change from 2000 to 2001 was negligibly small in the accumulation area. This conclusion was based on three findings: (1) The mass balance for the whole glacier for the period March 2000 to February 2001 was close to zero, at –0.06 m w.e. (Reference Skvarca, De Angelis and ErmolinSkvarca and others, 2004). (2) The mean elevation change over the accumulation area, corresponding approximately to the area surveyed in 2000, was ~0.7 m over the 11 years, equivalent to <0.07 m a–1 (Table 1). (3) According to static GPS measurements at seven stake locations the mean elevation change from 2000 to 2001 was 0.02 ± 0.13 m. As a result, the composite DEM from the 2000 and 2001 surveys represents roughly the surface at the end of February 2001. The second DEM represents the surface at the end of February 2011.
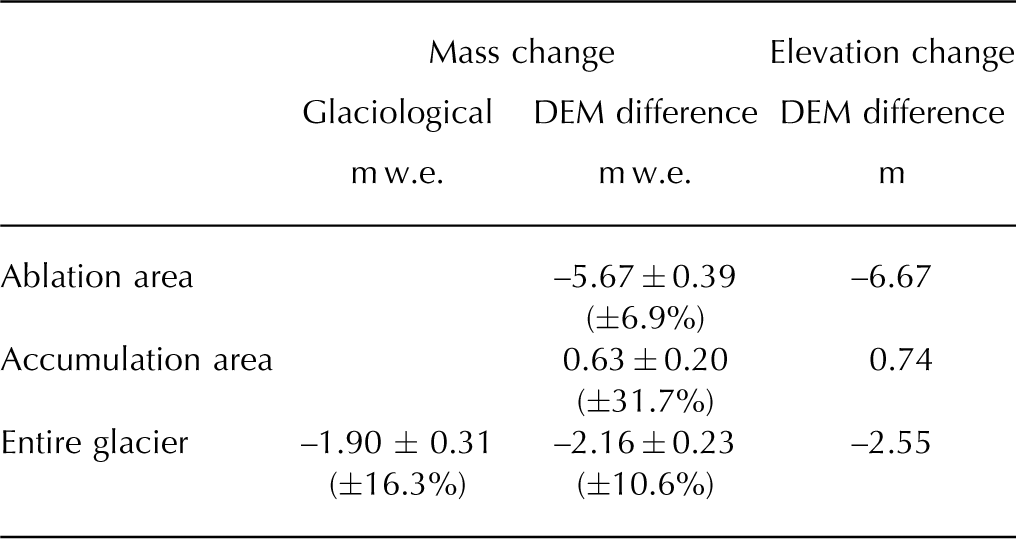
Table 1. Mass and elevation changes for the ablation, accumulation and entire glacier areas derived from the difference of 2001 and 2011 DEMs, and cumulative mass change during 2002–11 derived from annual surface mass balances by the glaciological method. Relative uncertainties are shown in parentheses
Both DEMs were produced with the same reference grid, and their difference provides an elevation change output at each gridpoint. The resulting matrix was filtered using an average filter with a kernel of 210 m × 210 m to smooth out the interpolation artifacts. An area near the nunatak (N in Fig. 1b) was excluded from the process because there are no reliable data in the area. There are high-slope icefalls which cannot be safely surveyed on snowmobile or foot. The excluded area was ~0.6 km2, corresponding to <5% of the total glacier area.
In the ablation area, the observed elevation change can be considered ice thickness change. In the accumulation area, elevation change may be attributed to either snow thickness change or vertical straining of ice beneath the snow layer due to glacier dynamics (Reference BaderBader, 1954). Because it was not possible to separate these two effects, a constant density of 850 ± 50 kg m–3 was used to convert the elevation change to mass change over the entire glacier surface (Reference Sapiano, Harrison and EchelmeyerSapiano and others, 1998).
Mass-balance determination by the glaciological method is known to have an uncertainty of 0.1–0.6 m w.e. (Reference JanssonJansson, 1999; Reference Zemp, Hoelzle and HaeberliZemp and others, 2009). On the other hand, we estimated the uncertainty in the geodetic mass change following a method similar to that proposed by Reference Huss, Bauder and FunkHuss and others (2009), using
where ρ = 850 kg m–3 and σρ
= 50kgm–3 are values for the density used to convert the volume to mass change and related uncertainty. ![]() represents the mean geodetic elevation change over the glacier for the whole period, and the uncertainty σz
introduced by the DEM differencing, also over the whole period, is given by
represents the mean geodetic elevation change over the glacier for the whole period, and the uncertainty σz
introduced by the DEM differencing, also over the whole period, is given by
where σDEM 1 and σDEM 2 are the uncertainties in the DEMs for the initial and final stages. Each of them has two main sources: the uncertainty in the vertical coordinate provided by the GPS measurement (σGPS) and the uncertainty associated with the interpolation algorithm (σInterpol). For the former we took the mean vertical uncertainty for the GPS data processed using the Trimble Pathfinder Office software, while for the latter we took the standard deviation of the cross-validation error of the interpolation process. The latter should be considered a lower bound for the interpolation uncertainty, because the data are not regularly spaced across the entire glacier. σGPS and σInterpol uncertainties are not independent. The data values on which the interpolation is based are all affected by the GPS vertical uncertainty. However, due to the difficulty of estimating the covariance between both variables we combined uncertainties as if they were actually independent, using
Results and Discussion
The mean elevation change for the whole glacier from 2001 to 2011 was –2.55 m, corresponding to –2.16 m w.e. after assigning densities as explained above (see also Table 1). Its associated uncertainty was calculated as follows. σInterpol for both DEMs was 0.10 m, as obtained from the cross-validation report generated by the interpolation software. The mean vertical uncertainty provided by the GPS processing software (σGPS) was 0.13 m for the 2000/01 set (11 500 points) and 0.11 m for the 2011 set (32 800 points). Then, using Eqn (3), σDEM 1 and σDEM 2 are respectively 0.16 m and 0.15 m, from which, using Eqn (2), we obtained a value of 0.22 m for the mean elevation change uncertainty σ z . Finally, using Eqn (3) and the density (and its uncertainty) given earlier, the resulting uncertainty estimate for the geodetic mass balance σgeod is 0.23 m w.e.
From field measurements, mean snow density for the whole period was 410 kg m–3, with a standard deviation of 3.8 kg m–3. Using the measured snow density, ablation and accumulation records, annual mass-balance maps were generated using the glaciological method, then linearly interpolated through the entire glacier surface (Fig. 3). The interpolation process produced mass-balance contours on each map, and the annual mass balance (m w.e.) was obtained from each for the hydrological years 2002–11. The mean mass change for the hydrological years 2002–11 derived from the glaciological method was –1.90 ± 0.31 m w.e., assuming an uncertainty of 0.1 m w.e. for the annual stake measurements (Reference JanssonJansson, 1999; Reference Zemp, Hoelzle and HaeberliZemp and others, 2009) (Table 2; Fig. 3).
Table 2. Annual mass balance (m w.e.) from 2002 to 2011 hydrological years for Glaciar Bahía del Diablo, Bellingshausen Ice Dome (Reference MavlyudovMavlyudov, 2014), Hurd Glacier and Johnsons Glacier (Reference Navarro, Jonsell, Corcuera and Martín-EspañolNavarro and others, 2013). The total mass loss is presented for each study period. The bottom row shows the Pearson correlation coefficient (r) between Glaciar Bahía del Diablo and the other glaciers
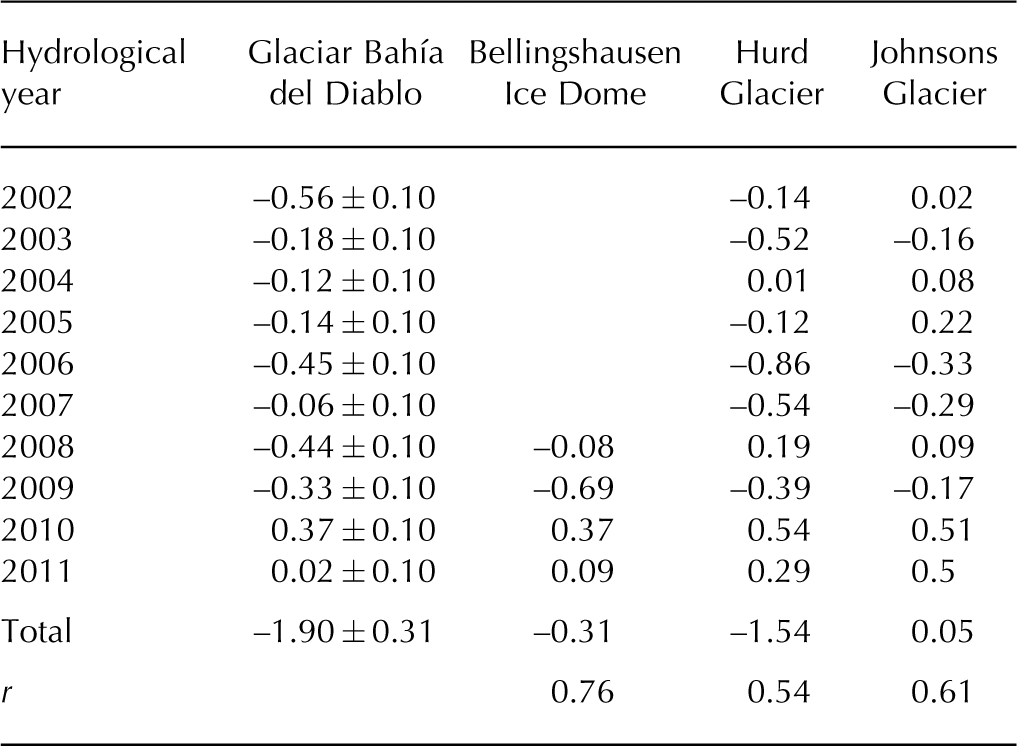

Fig. 3. Annual mass-balance maps determined by the glaciological method. Shading indicates positive balance, and white indicates negative balance.
Figure 4 is a map showing mass change, and Figure 5 shows mass changes vs surface altitude over the 2001–11 period based on the geodetic method. Changes are greater in the lower part of the glacier. The line corresponding to zero mass change in Figure 4 is very close to the 400 m a.s.l. contour, which corresponds to the previously reported ELA. Above this elevation, the elevation changes are smaller than in the lower reaches. Table 1 shows the elevation and mass changes over ablation and accumulation areas during the study period. The glacier-wide mean mass change is primarily controlled by the large mass loss in the ablation area. This result confirms the assumption used to construct the 2001 surface with data from the 2000 and 2001 campaigns.
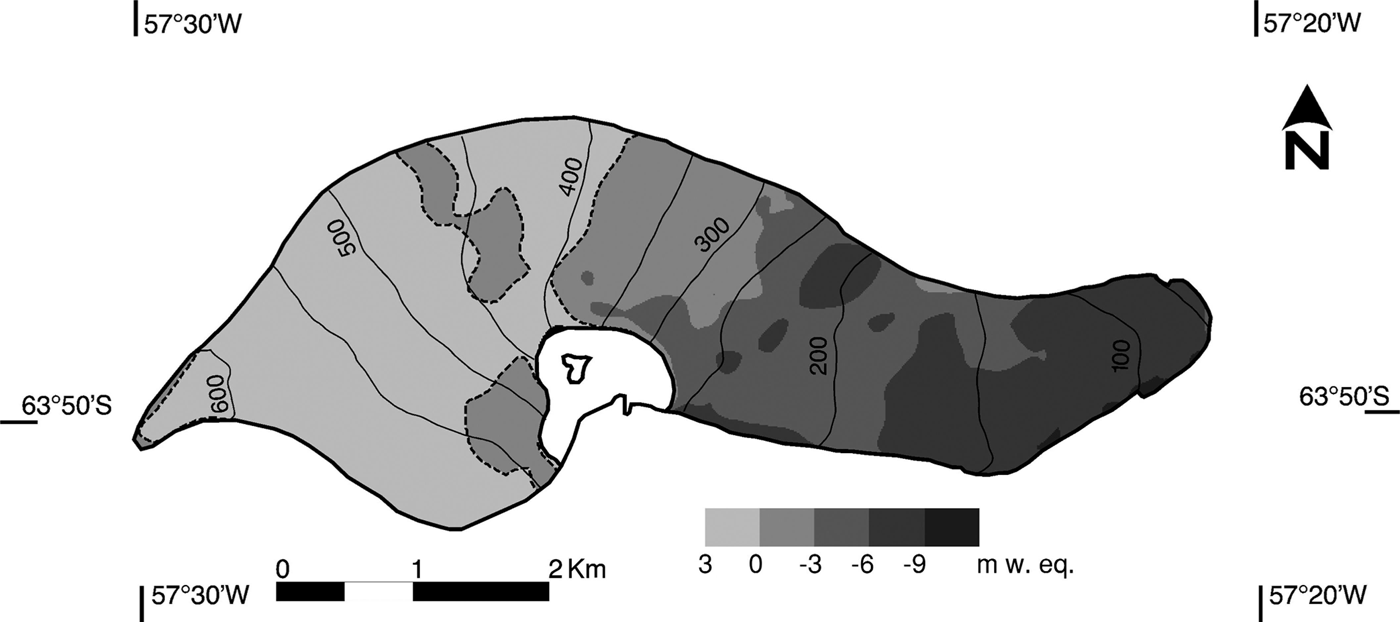
Fig. 4. Map showing cumulative mass change (m w.e.) in 2001–11 from DEM differencing. Blanks are non-surveyed areas near nunatak. Dashed lines indicate zero mass change. Surface elevation contours are in m a.s.l.
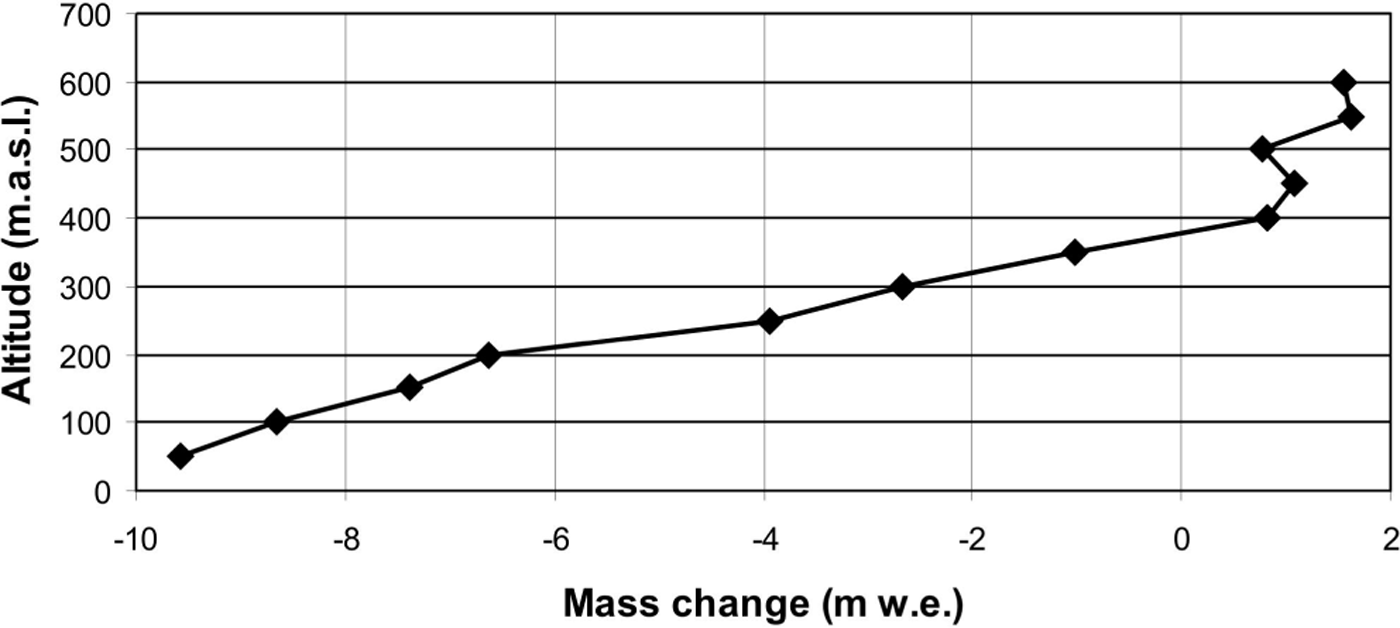
Fig. 5. Graph showing mass change vs altitude for 2001–11.
From the annual mass-balance maps (Fig. 3) and the total mass change for 2001–11 (Fig. 4) we can see that accumulation and ablation distribution over the glacier surface is well defined. The unusually high annual mass balance for the year 2009/10 with accumulation over the entire glacier surface was caused by an anomalously cold summer (Reference Costa and AgostaCosta and Agosta, 2012) with high precipitation during the first half, recorded at Marambio station. A few negative mass-balance sectors in the upper parts were recorded in 2002, 2006 and 2008 due to high mean summer air temperature. Except for these extraordinary values, the accumulation occurs mainly in the same sectors above the nunatak (N in Fig. 1b). In general, annual ELAs from 2002 to 2011 are in fair agreement with the previously reported ELA (400 m a.s.l.).
Annual mass-balance data from glaciers in the region are very scarce. For the period covered in the present work, mass-balance data are available for Hurd (4.03 km2) and Johnsons (5.36 km2) Glaciers on Livingston Island (Reference Navarro, Jonsell, Corcuera and Martín-EspañolNavarro and others, 2013), and over only the last 4 years for Bellingshausen Ice Dome (~8km2) on 25 de Mayo/King George Island (Reference MavlyudovMavlyudov, 2014) (Table 2). These glaciers are located on the western side of the AP, whereas Glaciar Bahía del Diablo is located on the eastern side. Different climatic regimes characterize the two sides of the AP, being continental on the eastern side and maritime on the western side (Reference SchwerdtfegerSchwerdtfeger, 1984). A very important difference in the climatic regimes is higher precipitation throughout the year on the western side. This feature may be responsible for the mass-balance difference between the glaciers. However, this is difficult to evaluate because Glaciar Bahía del Diablo is measured once per year, implying that only annual mass balance can be determined without separation of summer and winter balances. Conversely, at Johnsons and Hurd Glaciers, measurements are made at both the beginning and end of the melting season, so it is possible to estimate separate summer and winter balances. Glaciar Bahía del Diablo’s highest area is 630 m a.s.l., with a mean ELA at ~400 m a.s.l. The ice divide separating Johnsons and Hurd Glaciers has an altitude between 250 and 330 m a.s.l. with mean ELA at 228 and 187 m a.s.l. respectively (Reference Navarro, Jonsell, Corcuera and Martín-EspañolNavarro and others, 2013). The top of the Bellingshausen Ice Dome is 225 m a.s.l. and the ELA is ~200 m a.s.l. (Reference MavlyudovMavlyudov, 2014). Despite these differences, all four glaciers have shown similar behavior, especially in 2010 and 2011, when unusually positive annual mass balance was observed in all of the glaciers.
Conclusions
The most important conclusion is that the glacier mass changes obtained using the two independent methods agree with each other within the range of associated uncertainties. The cumulative mass change for the period 2001–11 is –2.16 ± 0.23 m w.e. for the geodetic method and –1.90 ± 0.31 m w.e. for the glaciological method.
The comparison of the two methods validates a series of annual surface mass balances obtained by the glaciological method, already reported to the WGMS database. The recommended calibration process of the annual mass balances from the glaciological method using geodetic volume change (Reference Zemp, Hoelzle and HaeberliZemp and others, 2009; Reference PaulPaul and others, 2013) did not require, in our case, any bias correction for the time series, as no significant difference between the two methods was found. Thus, this annual surface mass-balance series reported for Glaciar Bahía del Diablo can be considered reliable.
Acknowledgements
This study, including field campaigns and data analyses, was supported by different projects and programs funded by Instituto Antártico Argentino – Dirección Nacional del Antártico. We thank the people from Servicio de Hidrografía Naval and from Instituto Geográfico Nacional who participated in the field campaigns and helped carry them out. We thank the Scientific Editor Shin Sugiyama, Francisco Navarro, Daniel Nývlt and two anonymous reviewers for constructive comments and suggestions that helped to improve the manuscript.









