An Atmospherically Driven Sea-Ice Drift Model for the Bering Sea

Abstract

A free-drift sea-ice model for advection is described which includes an interactive wind-driven ocean for closure. A reduced system of equations is solved economically by a simple iteration on the water stress. The performance of the model is examined through a sensitivity study considering ice thickness, Ekman-layer scaling, wind speed, and drag coefficients. A case study is also presented where the model is driven by measured winds and the resulting drift rate compared to measured ice-drift rate for a three-day period during March 1981 at about 80 km inside the boundary of the open pack ice in the Bering Sea.

The advective model is shown to be sensitive to certain assumptions. Increasing the scaling parameter A for the Ekman depth in the ocean model from 0.3 to 0.4 causes a 10 to 15% reduction in ice speed but only a slight decrease in rotation angle (α) with respect to the wind. Modeled α is strongly a function of ice thickness, while speed is not very sensitive to thickness. Ice speed is sensitive to assumptions about drag coefficients for the upper (C_A) and lower (C_W) surfaces of the ice. Specifying C_A and the ratio of C_A to C_W are important to the calculations.

Introduction

The Bering Sea has the largest continental shelf area in the world apart from the Arctic Ocean, and supports the largest commercial fishery. In addition, portions of the shelf are scheduled for intensive oil exploration, and the region is a thoroughfare for barge traffic for the western Arctic. Since the Bering Sea supports a seasonal sea-ice cover from late October to late June, it is important for safety and economy that sea-ice forecasts be improved for the area. Although we are developing a full regional model with both dynamical and thermodynamic sea-ice calculations, in this paper we present only a simple candidate model for the advection of ice. This model is an extension to the coupled ice/ocean models of Reed and Campbell (1962) and Neralla and others (1980). This simple scheme may be useful for climate research models desiring an interactive ice cover.

Model Description

In the Bering Sea during winter away from land, sea-ice floes are generally drifting freely in response to the wind. Currents away from straits and the shelf break are relatively weak. Consequently a good first-guess model for ice velocity can be derived from the free-drift approximation, i.e. for individual Lagrangian elements, for the stress balance on sea ice,

(1)

where _A and _W are the tangential surface stresses at the air and water interfaces, i² = −1, ρI is the density of the ice, H_I is the thickness of the ice, f is the Coriolis parameter, and _I is the ice velocity. We assume that the surface stresses can be parameterized by quadratic drag laws

(2)

and

(3)

where ρA and ρW are air and water densities, C_A and C_W are empirically determined drag coefficients and _A and _W are the Eulerian wind and wind-driven current. We consider C_A and _A relative to the reference level at 10 m and C_W and _W relative to the reference level (h_W) at 2 m. Note that _A – _I and _W – _I are the Lagrangian velocities that would be measured by instruments attached to an ice floe at those levels.

Given that we can estimate the other variables, _I and _W are the unknowns, so we need an additional relation to close the system of equations. We establish another expression for _W and _W by modeling the ocean with a constant stress surface layer with a linearly increasing eddy coefficient and logarithmic velocity profile to a depth h and then an Ekman layer for an infinitely deep ocean. Let

(4)

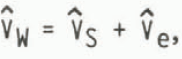
where the surface-layer contribution to the velocity is

(5)

and where the Ekman (1905) velocity at depth h is

(6)

In Equation (5), _* is the friction velocity defined by

(7)

k = 0.4 is Von Karman’s constant, and z_W is the roughness length for the bottom of the ice defined by

(8)

In Equation (6), D is the Ekman depth approximated by

(9)

where A is the scaling factor of 0.3 (Blackadar and Tennekes 1968). To specify the depth of the surface layer h, we use h = δD where δ = 0.1 (McPhee and Smith 1976). A schematic of the modeled ocean relative to the ice and the bottom is given in Figure 1.

Fig. 1 Schematic diagram of the modeled ocean relative to the ice and the sea bottom.

By making appropriate substitutions and rearranging terms, the Equations (1) through (9) can be reduced to Equation (7) and

(10)

and

(11)

The three unknowns in (7), (10), and (11) are _W, _*, and _I, and the solution for the coupled nonlinear system can be obtained by iterating on _W. A first-guess , and the iterative closure criterion is _W – _W (old guess) / _W < ε. For ε = 10⁻⁵, closure occurs in 5 to 7 iterations.

Model Sensitivity

The model was run for a range of variables to test the sensitivity for future forecasting applications. A list of the model parameters used for a standard or reference case are given in Table I.

Table I Values for Model Variables for Standard Case

Although most of the unridged ice in the Bering Sea has a thickness of 1 m or less, it is helpful to examine the response to a range of thicknesses (Fig.2) both to facilitate comparison with other models and to evaluate its probable performance for other oceans. The modeled ice velocity varied linearly with changes in thickness. Speed decreased by 0.05 m s⁻¹ for each 0.3 m increase in thickness and rotation of the ice motion to the right of the wind stress a increased 1.5° for each 0.3 m increase in thickness. As expected, water velocities had the same trends as ice velocities. These results agree with McPhee (1982).

Fig. 2 Variations in ice velocity for a range of thicknesses of sea ice and for two different assumptions for the Ekman depth-scaling parameter A.

In Figure 2 we also show the effect of variation of the Ekman scaling parameter A. The range for A in the literature is 0.3 to 0.4. For ice 1 m thick, the modeled ice speeds differed by 0.07 m s⁻¹ and 4°. The larger the Ekman depth for a given applied stress, the slower the ice drifted and the less 1t rotated to the right of the wind.

Figures 3 and 4 show the results for varying the drag coefficients. The sea ice in the Bering Sea is rough aerodynamically because of the existence of many small roughness elements. Measurements for the area suggest that C_A = 2.8 x 10⁻³ and C_w = 16 x 10⁻³ in the interior and both are proportionately higher in the marginal ice zone (Macklin 1983, Pease and others 1983, Walter and others in press). Generally, if C_w is increased by 5 x 10⁻³ for constant C_A, the predicted ice speed drops by about 0.05 m s⁻¹, but α increases only slightly. If C_A is increased by 1.0 x 10⁻³ for constant C_w, then the predicted ice speed increases by 0.10 m s⁻¹ and α decreases slightly. If C_A and C_W, vary proportionally, due in some sense to isostatic equilibrium, then these results show that increased total roughness causes an increased ice speed but little change in angle, even though the drag on the water increases also.

Fig. 3 Variations in ice velocity for a constant air-ice drag coefficient but varying ice-water drag coefficient for two ice thicknesses.

Fig. 4 As in Figure 3, except varying the air-ice drag coefficient.

We need to examine the model dependence on wind speed so that we can evaluate the impact of errors in wind velocity on the estimates of ice velocity. Figure 5 shows speed and rotation angle for a range of wind speeds for floes that are 1 and 3 m thick. The rotation angle is sensitive to changes in wind speed for moderate to light winds. This effect is enhanced for the thicker ice. Variations in speed are nearly linear for thin ice, but nonlinear for low wind speeds for thicker ice. Instances where the wind velocity is low are difficult to evaluate with field data because unmodeled physics, such as small steady currents, tidal and high-frequency accelerations, and sea-surface tilts, become important.

Fig. 5 Variations in ice velocity for a range of wind velocities for two ice thicknesses.

Case Study

An experiment was conducted near the ice edge during 1981 in which a floe was instrumented with anemometers, current meters, and an ARGOS satellite position transponder. Additional details about the experiment can be obtained from Macklin (1983) and Pease and others (1983). The measurements were averaged to hourly data for a total of 65 samples. The ARGOS positions were fitted with a cubic spline and resampled for the same period, and ice velocities were calculated by central-differencing the resampled positions. In order to remove the tidal signal from this short record, we fitted a broad quadratic to the series to mimic the longer period change in the velocity. In a follow-up experiment in 1983, we took longer time-series measurements which will allow us to perform additional validation studies with ice velocities which have had tidal signals removed by more conventional means.

The wind blew from the north-east and ice drift was toward the west-south-west throughout the 1981 measurements. The maximum wind and floe velocities were mid-period. The range of wind speeds was 6 to 12 m s⁻¹ and averaged 10.4 m s⁻¹ (SD = 2 m s⁻¹). The ice was approximately 1 m thick; A, C_A and C_W for the model run were set to the values listed in Table I. The results of the model run compared to the observed velocities are given in Table II.

Table II Observed and Modeled Ice and Water Velocities

The model overestimated current velocity uniformly and underestimated the current angle, but the correlations with ice velocity were excellent. Thus we have an overall bias in current velocity which may be due to A, C_W, or unmodeled physics. This bias will be considered more fully in future work.

Summary

The candidate model for sea-ice drift described in this brief article is intended to be applied to sea-ice forecasting and climate problems in the Bering Sea. Its strengths include that (1) it does not require a priori knowledge of currents other than that they are largely wind-driven, (2) its calculation time is sufficiently short that it is economical to run, and (3) it contains the firstorder ice physics necessary to predict ice motion over an open continental shelf. Its weaknesses include that (1) it is somewhat sensitive to certain empirical parameters such as the Ekman depth scaling, drag coefficients, and ice thickness, (2) it does not contain sufficient ice physics to be useful near land where internal ice stress may be important, and (3) it does not contain sufficient ocean physics to be useful for very shallow water or for regions where currents that are not wind-driven are important. Overall, the performance of this drift model in sensitivity studies and in comparisons to field data is encouraging for forecasting applications.