An automatic approach to delineate the cold–temperate transition surface with ground-penetrating radar on polythermal glaciers

Abstract

Ground-penetrating radar has been widely used to map the thermal structure of polythermal glaciers. Hitherto, the cold–temperate transition surface (CTS) in radargrams has been identified by a labour-intensive and subjective manual picking method. We introduce a new automatic approach for picking the CTS that uses the difference in signal power exhibited by the cold and temperate ice layers. We compare our automatically computed CTS depths with manual picks. Our results show very good agreement between the two methods in most areas (r² > 0.7). RMSEs computed at each trace in two-way travel-time from three test sites range from 14 to 19ns (2.4–3.2 m). The proposed automated method mostly fails in areas showing a rather gradual transition in signal power at the CTS. In some areas, high power originating from non-water sources is misinterpreted by the automatic picking method as ‘temperate ice’.

Introduction

Polythermal glaciers are prevalent in polar, subpolar and mountainous regions (e.g. Huang, 1990; Björnsson and others, 1996; Suter and others, 2001; Rabus and Echel-meyer, 2002; Pettersson and others, 2003; Gusmeroli and others, 2013). Such glaciers consist of temperate ice at the local pressure-melting point (pmp) and cold ice which is below the local pmp. Both ice types exhibit distinct properties, in particular water content. In temperate ice, water and ice coexist at a variety of scales ranging from interstitial water (up to 7% by volume) to larger water bodies in the form of conduits, water-filled crevasses and fissures, while only the larger water-containing features may be found in cold ice (Pettersson and others, 2003, 2004; West and others, 2007; Gusmeroli and others, 2010).

The englacial boundary between cold and temperate ice is known as the cold–temperate transition surface (CTS). The CTS separates water-free cold ice from wet temperate ice (e.g. Pettersson and others, 2004; Gusmeroli and others, 2010), and constitutes a dielectric boundary that can be detected and mapped by ground-penetrating radar (GPR) systems (e.g. Björnsson and others, 1996; Moore and others, 1999; Moorman and Michel, 2000; Murray and others, 2000). In GPR data, this commonly leads to a two-layered structure. However, more complex thermal structures can also occur (Murray and others, 2000; Irvine-Fynn and others, 2011). The cold ice layer is characterized by few internal reflectors or scatterers and is thus rather transparent to the radar wave, whereas the temperate ice layer contains numerous reflections and therefore appears opaque in radargrams. Although a variety of scatter sources are present in glaciers (Jacobel and Raymond, 1984), the vast majority of the scatterers in temperate ice are assumed to be water inclusions (Bamber, 1988; Hamran and others, 1996). This means that a scatter-rich layer is an indication of water distribution rather than temperature (Brown and others, 2009; Irvine-Fynn and others, 2011). On Stagnation Glacier, Bylot Island, Canada, short-term changes in the scatter-rich layer were interpreted as temperate ice becoming drained during the course of the melt season (Irvine-Fynn and others, 2006) rather than a change in thermal regime. However, the scatter-rich layer is commonly associated with temperate ice. Borehole temperature measurements taken in Svalbard (Ødegȧrd and others, 1997), Arctic Sweden (Pettersson and others, 2003; Gusmeroli and others, 2012) and the European Alps (Ryser and others, 2013) confirm that the depth of the 0˚C isotherm and the top of the scatter-rich layer agree with each other within the error bars of each measurement.

The position of the CTS changes over time and is determined by the glacier's heat balance (Cuffey and Paterson, 2010). Climatic variations are the main driver for changes of the heat balance of glaciers (Pettersson and others, 2007; Wohlleben and others, 2009). Very different responses of the thermal regime of polythermal glaciers to climate warming over the past few decades have been reported (Moorman and others, 2004; Irvine-Fynn and others, 2011; Gilbert and others, 2012; Gusmeroli and others, 2012). Trends range from significant thinning and recession of the cold surface layer on Storglaciären (Gusmeroli and others, 2012) to significant thinning and recession of the temperate layer on Glacier de Tête Rousse, France (Gilbert and others, 2012). These opposing responses show that changes in thermal regime result from complex interactions between environmental factors, such as location, climate, study period considered and a combination of climate-induced and dynamics-related (e.g. strain-heating) changes (Irvine-Fynn and others, 2011).

Hitherto, the CTS has been picked on radargrams by a labour-intensive manual picking method (Pettersson and others, 2007; Eisen and others, 2009; Gusmeroli and others, 2012). This method always introduces some subjectivity to the pick and is, furthermore, not easily reproducible (Pettersson and others, 2003). Attempts to quantify the amplitude difference in radargrams between cold and temperate ice are scarce. Gusmeroli (2010) undertook experiments, picking the CTS automatically by locating the maximum amplitude between the airwave and the manually picked bed reflector on each trace. This experiment was repeated with half of the maximum amplitude as well as one-third of the maximum amplitude on each trace. However, no coherent CTS could be successfully picked, as the noise level for point scatterers often exceeded single amplitudes in the scatter-rich layer. As part of a quantitative demonstration, Brown and others (2009) calculated signal-to-noise ratios (SNRs) in the transparent and in the scatter-rich layer of a radargram from Bench Glacier, Alaska, USA, using

(1)

where P _signal is the mean power of the radar signal calculated in a time window within the cold or temperate ice layers, and P _noise represents the power of the noise, calculated as the power of the signal recorded in a time window spanning all the period before the direct airwave arrival. Power values are defined as the square of the amplitudes. Using Eqn (1), Brown and others (2009) reported an increase in SNR from 6.7 dB to 17.6 dB when passing from the transparent layer to the scatter-rich layer.

In this paper, we present an approach that automatically picks the CTS on radargrams, based on the previous quantitative demonstration by Brown and others (2009). This automatic picking method utilizes the difference in signal power exhibited by the cold and temperate ice zones and incorporates it into a numerical algorithm which was coded in MATLAB^®. To validate the results of the automatic method, the automatic picks were compared with manual picks of the CTS carried out by a geophysicist who did not know the results from the automatic picking method.

RADAR Data Acquisition Sites

In order to assess the general applicability of the automatic picking method, we tested the algorithm on radargrams from three different glaciers with different environmental settings: Midtre Lovénbreen in a polar setting, Storglaciären in a subpolar setting and Glacier de Tsanfleuron in a mountainous setting. We note that, although in different environments, all three test sites have undergone considerable retreat over the past few decades (Holmlund and others, 1996; WGMS, 2008; James and others, 2012).

Midtre Lovénbreen is a small polythermal valley glacier, located 5km southeast of Ny-Alesund in Svalbard (Fig. 1a). Its areal extent in 2005 was 5.1 km² and the length of the glacier along the centre flowline was 4.4 km. The maximum ice thickness was 180m. GPR surveys demonstrated that the glacier has a temperate core with a maximum thickness of 50m, which is overlaid by a thick cold ice surface layer (Björnsson and others, 1996). The temperate core is thinnest towards the margins, and the lowest 1 km of Midtre Lovénbreen consists entirely of cold ice (Björnsson and others, 1996).

Fig. 1. Landsat-7 (band 3) images of the three study areas. Solid black lines show location of GPR survey lines. Coordinates are in Universal Transverse Mercator (UTM). (a) Midtre Lovénbreen (UTM zone 33), Svalbard, in July 2002. Glacier flow is upwards. (b) Storglaciären (UTM zone 34), Sweden, in September 2000. Glacier flow is from left to right. (c) Glacier de Tsanfleuron (UTM zone 32), Switzerland, in July 2001. Glacier flow is from left to right.

Storglaciären is a well-studied polythermal glacier in northern Sweden (Fig. 1b). The glacier covers an area of 3.1 km², is 3.2 km long and has a maximum ice thickness of 260m (Jansson, 1996; WGMS, 2011). The thermal structure has been extensively mapped using GPR over the past two decades (Holmlund and Eriksson, 1989; Pettersson and others, 2004, 2007; Gusmeroli and others, 2012). These studies have shown that the vast majority of the ice is temperate and only a small area in the ablation zone is covered by a cold ice surface layer (Gusmeroli and others, 2012). The maximum thickness of the temperate core is >200 m and the temperate ice thins towards the terminus and towards the margins of the glacier (Gusmeroli and others, 2012).

Glacier de Tsanfleuron is located in the western Bernese Alps, Switzerland (Fig. 1c). It is a small mountain glacier which covers a surface area of 3.5 km² and is 3.7 km long (Hubbard and others, 2003; WGMS, 2008). Its maximum ice thickness is 140 m. GPR surveys undertaken in 2004 confirmed previous observations from Hubbard and others (2003) that the glacier has a two-layered thermal structure, with radargrams very similar to those of polythermal glaciers (Murray and others, 2007). The thickness of the transparent layer varies between 7 and 42m along the transverse profile (Murray and others, 2007).

Methods

GPR surveys

Common-offset radar surveys on Midtre Lovénbreen, Storglaciaren and Glacier de Tsanfleuron were used to test the automatic picking algorithm. The radar data on Midtre Lovénbreen were acquired in spring 2000, spring 2008 and spring 2011; the same radar lines were surveyed in all three years (Fig. 1a). The radar data on Storglaciären and Glacier de Tsanfleuron were acquired in spring 2009 and spring 2005, respectively. Important acquisition parameters of all radar surveys are summarized in Table 1.

Table 1. Summary of GPR survey parameters (ML: Midtre Lovenbreen)

GPR processing differed from glacier to glacier due to the use of different GPR systems, but processing steps were consistent for all profiles on the same glacier. Furthermore, processing was adjusted, such that the CTS was most distinctive. Table 2 summarizes processing steps applied on each data series. A high-pass filter was used to remove low-frequency instrument generated noise. Kirchhoff migration on Midtre Lovénbreen was applied using a velocity of 0.167 m ns^–1. This is very similar to velocities used previously on Midtre Lovénbreen radar data (Hambrey and others, 2005; King and others, 2008). Migration was not applied on the other two test sites because (1) on Storglaciären trace spacing was uneven and migration did not change the position of the CTS (Gusmeroli and others, 2012), and (2) traces on Glacier de Tsanfleuron showed few scatterers in the transparent layer, making migration redundant. We note that differing processing steps from site to site lead to different signal power in the transparent and scatter-rich layers.

Table 2. Summary of GPR processing applied to the three study areas

Automatic picking method

The automatic picking method presents as follows. As first step, a reference reflector, typically the glacier bed, was manually picked in ReflexW (Version 6.1.1, by Sandmeier Software). The automatic picking method then works up from the respective reference reflector (Fig. 2). As long as this reference reflector is within the temperate ice layer, it does not affect the automatic CTS pick. However, if the reference reflector coincides with the glacier bed, it then allows the bonus of calculating the thickness of the temperate ice layer. On Midtre Lovénbreen, glacier bed and reference reflector coincided, whereas on the other two test sites an arbitrary level within the temperate ice was used, as the GPR did not penetrate deep enough to record the glacier bed. In the following, both starting-point methods are referred to as a reference reflector.

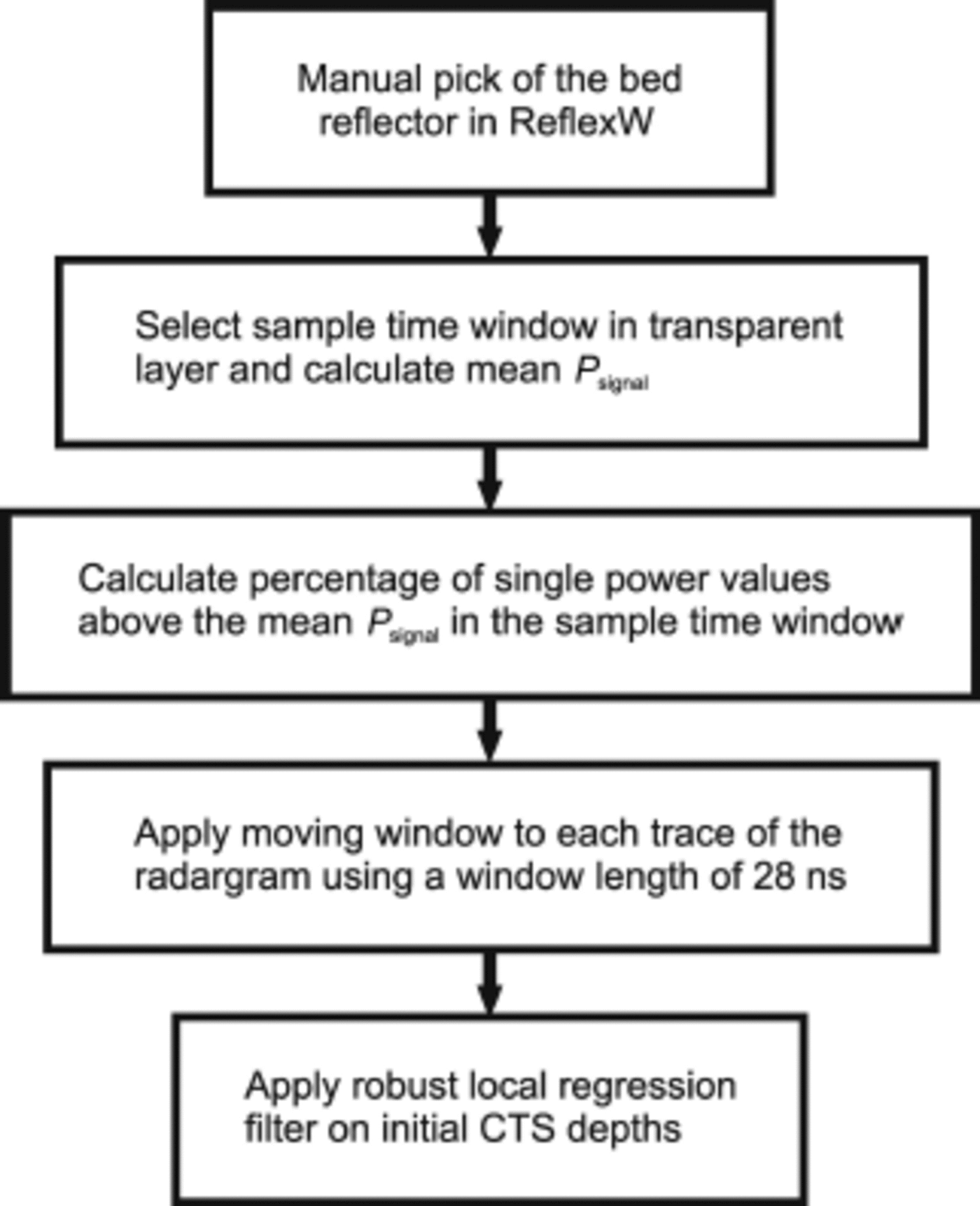
Fig. 2. Schematic flow diagram of the automatic picking method.

In the second step, a representative sample time window (Figs 3 and 4) was selected in the transparent layer of the radargram (Fig. 2). The position of the time window did have some effect on the final CTS pick. However, as long as areas with uncharacteristically high amplitudes (e.g. discrete scatterers or the airwave) were avoided, computed CTS picks were almost identical. The black boxes in Figures 3 and 4 show sample time windows used for the respective radargrams and provide an example of the suitable size for sample windows. Different sample window sizes were used to investigate potential effects on the automatic pick. Our results show that varying the size of the sample window leads to negligible deviations in the automatic CTS pick. After selection of the time window in the transparent layer, the mean power value (P _signal) of the sample box was calculated (Fig. 2) and the percentage of signal power values above the mean signal power of the sample window was determined (PC_sample). This calculated percentage then served as the threshold for determining the CTS in each trace. Here signal power values instead of SNRs were used because in some radargrams there were almost no pre-airwave recordings, making the calculation of SNRs impossible.

Fig. 3. (a, c) Fully processed sample radargrams (a) LONG1 (ice flow left to right) and (c) TRAN2 (ice flow out of page), from Midtre Lovénbreen, with black boxes approximating locations of sample window in the transparent layer. In (a) and (b) black line shows automatic CTS pick before and after application of the smoothing function. (d) Zoom of the same radargram as in (c) with the smoothed automatically picked CTS (solid line) and manually picked CTS (dashed line). Amplitude scale is in mV².

Fig. 4. (a, c) Fully processed radargrams (a) P24 (ice flow into page) of Storglaciären and (c) P1 (ice flow out of page) of Glacier de Tsanfleuron, with black boxes approximating locations of sample window in the transparent layer. (b, d) Zooms of the same radargrams in the background with the smoothed automatically picked CTS (solid line) and the manually picked CTS (dashed line). Amplitude scale is in mV².

In the next step, a moving time window was applied to each trace individually from the reference reflector upwards (Fig. 2). The optimal length for the moving time window was calibrated on the first analysed radargram from Midtre Lovenbreen. The window length that coincided best with the CTS visible in the radargram was 28 ns. In three radargrams from Storglaciären, a different window length was used due to a very thin transparent layer which caused overrunning of the CTS when using a window length of 28 ns. However, if not stated otherwise, a window length of 28 ns was used. In the moving window, the percentage of signal power values above P _signal was calculated (PC_mov). As long as PC_mov ≥ PC_sample, the moving window was moved vertically upward by one sample in the radar time trace. When PC_mov<PC_sample, the lowest point in the moving time window was marked as the CTS and the algorithm moved on to the next trace. This process was carried out for all traces in the radargram.

Finally, in order to reduce the effect of miscomputed CTS depths on the final CTS pick on each trace, we used the smooth’ function in MATLAB^® http://www.mathworks.co.uk/help/curvefit/smooth.htmlSeveral Several smoothing methods are available within this function. In this study, a local regression filter worked best (Fig. 2). The span of the local regression filter was 20 traces (~10 m lateral distance) for all radargrams. The filter assigns regression weights to each of the computed CTS depths in the span. The highest regression weight is always assigned to the trace to be smoothed. All CTS depths outside the filter span are assigned zero regression weights. In the filter span, a linear-least-squares regression is carried out. The local regression filter was used in the robust mode. As well as calculating the regression weights, this mode determines the robust weights in the filter span. These robust weights are resistant to outliers, and therefore considerably improved our final CTS pick. For a more detailed description of the smoothing function, the reader is referred to the MATLAB^® Help.

Manual picking method

In order to allow a comparison of our results with the traditional manual picking method, the CTS was also manually picked on all radargrams. On Storglaciären, the manual picks from Gusmeroli and others, 2012 were used. In that study, the CTS in a radargram was picked 30 times and the mean of the 30 picks was selected as the best-fitting CTS pick. At the other two sites, the CTS was picked once manually by A. Gusmeroli without prior knowledge of the automatic picks. We did not use multiple picks on Midtre Lovenbreen and Glacier de Tsanfleuron, as reported deviations are ≤±0.8m (Pettersson and others, 2003; Gusmeroli and others, 2012).

Results

In order to test the general applicability of the automatic picking method, the code was applied to data from the three different test sites. Computed CTS results of three sample profiles are shown in Figures 3 and 4. In general, the automatic picking method follows positive peaks as well as troughs of the CTS quite closely. The high signal power exhibited in the eastern part (traces 1400–1500) of the Midtre Lovénbreen sample radargram (Fig. 3c) close to the bed reflector is not attributed to temperate ice but represents distortions introduced by the migration process. The automatic picking method was unable to detect whether the high signal power in the radargram originated from reflections of water bodies or from artefacts introduced by the processing applied. Thus, the algorithm is only applied in regions where the manual pick identified the presence of temperate ice.

Uncertainty Assessment

Tie-point analysis

For each acquisition date – 2000, 2008 and 2011 – there were two tie points present on Midtre Lovénbreen (Fig. 1a). In order to assess the uncertainty associated with the automatic picking method, the automatic CTS was corrected for the error in picking the bed reflector. Since the bed reflector was picked manually within ReflexW, slight deviations occurred at the tie points. These deviations propagated into the thickness calculations of the temperate ice body which were used to assess the consistency of the automatic picking method. Hence, the deviation between the depths of the bed reflector at the tie points was either subtracted from or added to the calculated temperate ice thickness. The analysis of the tie points reveals slight deviations from year to year. The lowest deviation was observed in 2008 with a root-mean-square error (RMSE) of 1.5 m, whereas the highest RMSE of 2.4 m was observed in 2000. The mean RMSE over all six tie points of the different years gives a RMSE of 2.2 m. However, this value could be slightly over- or underestimated depending on the roughness of the glacier bed at the tie points and the difference in surface position of the tie-point traces.

Comparison between manual and automatic picking methods

We note that the comparison between the manual method and the automatic method does not aim to compare the correct pick (manual method) with the modelled pick (automatic method). It is rather an approach to assess how large the deviations between the two methods are and compare these deviations with the maximum accuracy that can be reached using GPR on polythermal glaciers.

Figures 3 and 4 show the comparison between the automatic (solid line) and manual (dashed line) picking method for the three sample profiles. Correlation analysis reveals that on the vast majority of the profiles, automatic pick and manual pick are in very good agreement with each other (r ²>0.7). Only one profile, on Midtre Lovenbreen, exhibits no correlation between the two picks. Despite this generally good agreement, there are regions in the radargrams where significant deviations between automatic and manual pick occur. For instance, in Figure 3d, high deviations can be observed at the margins of the temperate ice layer (traces 500-800). The trend of highest deviations occurring at either margin of the temperate ice layer continues for all profiles on Midtre Lovenbreen but is absent in the profiles from the other study sites (Fig. 3).

Highest deviations on Storglaciaren and Glacier de Tsanfleuron occur in areas where reflections from point scatterers obscure the actual CTS (e.g. Fig. 4b, traces 25003500) and where the power difference between the scatter-rich and transparent layer is rather gentle (e.g. Fig. 4d, traces 1000-1500). This becomes especially problematic for the automatic picking method, if the general signal power drop from the scatter-rich to the transparent layer in the radargram is strong. In this case, the automatic pick tends to underestimate the CTS (Fig. 4d). A general trend throughout the dataset was that the best fit between the automatic and manual picking methods was observed in areas where the CTS depth did not show much lateral variation (Fig. 3d and 4d).

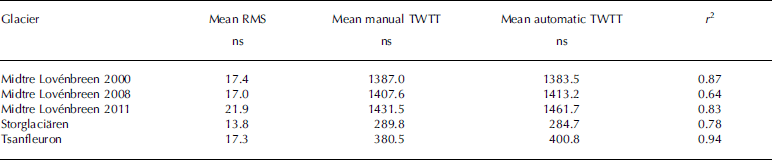
Mean RMSEs calculated in two-way travel-time (TWTT) at every trace in each radargram lie in a very similar range for all three test sites. This indicates that the use of different radar systems does not significantly affect the uncertainty of the automatic picking method. In general, a larger spread in mean RMSEs was observed on Midtre Lovenbreen than on Storglaciaren. The RMSE observed on Midtre Lovénbreen ranged from 9.7 to 32.2 ns (1.6-5.4 m), whereas on Storglaciaren the RMSE only varied from 10.5 to 16.7 ns (1.8-2.8 m). The main reason for the higher RMSE values on Midtre Lovenbreen is the high deviations that occur at the lateral margins of the temperate ice body. Possible causes for this could be differing GPR processing (bandpass filter and/ or migration) or the use of different GPR systems. We believe differing processing is more likely, as migration of radar-grams on Midtre Lovénbreen introduced noise in some of the radargrams, complicating picking of the CTS.

In spite of the observed deviations, when calculating the mean overall profiles for the manual as well as the automatic method, the deviations usually disappear almost completely (Table 3). This increases the confidence in the presented automatic picking method and, furthermore, indicates that the deviations between the two methods are randomly distributed. Only on Midtre Lovénbreen in 2011 are significant deviations observed. Although this could be due to the different GPR system used in that year, we believe that this is rather unlikely because the high observed value is due to a single very noisy profile where the manual pick underestimates the CTS considerably. When omitting this noisy profile from the analysis, the deviation is very similar to that in previous years (<7ns).

Table 3. Summary of RMS, mean CTS depth in TWTT, and correlation coefficient (r ²) for the three test sites

Comparing the manual picking method with the automatic picking method does not evaluate the uncertainty between the physical CTS and the interpreted CTS. In order to accomplish this, the picked CTS, no matter if picked manually or automatically, needs to be compared to temperature measurements of a thermistor string in a borehole. Various errors in depth of the CTS have been reported ranging from ±4 m to ±1 m (Ødegård and others, 1997; Pettersson and others, 2003; Gusmeroli and others, 2012). The former high value is mainly due to a poor vertical resolution of the thermistor string (Ødegård and others, 1997) and is therefore assessed as not representative for this study. The latter value is most likely too optimistic for our study to be representative because Pettersson and others (2003) used GPR systems at frequencies of 800 and 345 MHz which provide a better vertical resolution, so the CTS can be picked more precisely. Gusmeroli and others (2012) reported that the CTS picked in the radargram agrees with the CTS measured in the borehole within ±2 m. Since they used a GPR at 100 MHz, it is assumed to be the most representative. Assuming a velocity of 0.168mns–1 in cold ice gives an error range of 23.8 ns. This means that the deviations between the manual and automatic methods are roughly in the range at which the CTS can be reliably determined in a radargram using a centre frequency of 100 MHz.

Despite showing promising results, a few shortcomings of the automatic picking method exist. Firstly, all three study sites represent somewhat ‘ideal’ polythermal glaciers without debris cover and free of significant lateral and medial moraine forms. Moreover, all test sites exhibit a relatively simple two-layered thermal structure. Both characteristics greatly facilitate GPR surveying and simplify the analysis of the CTS in radargrams. Secondly, high signal power originating from other sources than water in the temperate ice layer (e.g. large crevasses, rock entrainments) might be misdetected as ‘temperate ice’. There is no automatic or indeed manual solution to this problem yet. However, the length of the moving window can be adjusted manually to at least reduce the effect of this high signal power. Thirdly, the algorithm can only be applied to radargrams that have a transparent layer of a certain minimum thickness. On glaciers with a very thin cold surface layer where ‘ringing’ at the CTS is still present (Fig. 3a), the method sometimes fails to produce reasonable results. Fourthly, although Pettersson and others (2003) reported that CTS measurements on Storglaciaren within ±21 m are usually at very similar depths (within ±1 m), this might not be the case on other polythermal glaciers or at the margins of the temperate ice layer. The maximum thickness of the CTS on the three test sites is ~160m, which leads to a horizontal resolution of ~15m with a 100MHz GPR system. If the CTS is steeply inclined in this region, it can lead to significant alterations in CTS depth.

Conclusions

We have developed an automatic method to pick the CTS in radargrams that is applicable on simple two-layered polythermal glaciers. Using the automatic picking method significantly reduces the subjectivity of the CTS pick, and, furthermore, the CTS pick is easily reproducible. Uncertainty assessment from three different test sites revealed RMSEs of 13.8–18.9 ns (2.3–3.2m) in comparison with manually picked values. With the restrictions discussed earlier, comparing these values to the nominal depth accuracy reachable when using a 100MHz GPR system (23.8 ns) shows that the deviation between the manual and automatic methods is in a similar range to the reported depth accuracy. Furthermore, the automatically picked CTS depth may show trends of underestimation or overestimation in single profiles (Fig. 3d). Yet, when averaging over a number of radargrams from the same glacier, these trends diminish.