Introduction
The mass balance of Arctic glaciers is a crucial indicator of climatic change. The most important factor responsible for determining glacier mass supply is winter snow accumulation. The accumulation at the end of the winter season at any point on the glacier is a function of gains and losses of snow during this period. In winter, snowfall is the main control on glacier mass. Other factors influencing net winter accumulation (e.g. snowdrift, sublimation, melting and avalanche supply) are much less important than winter snowfall. Thus, it is assumed that the snow accumulation at a given point on a glacier is approximately equal to the sum of precipitation over a given period. The attempt at assessing the snow accumulation can be boiled down to the task of determining the total amount of precipitation in a season of accumulation. In this paper, I present a simple model for snow accumulation on Svalbard glaciers. The aim is to estimate local snow accumulation based on location, altitude, and data from a nearby permanent weather station.
Spatial distribution of the snow cover on Svalbard’s glaciers has been examined in many ways on the basis of numerous field surveys, on both regional and local scales (Reference Mikhaliov and SingerMikhaliov and Singer, 1975; Reference Khodakov and KotlyakovKhodakov, 1985; Reference Migała, Pereyma, Sobik, Jania and PulinaMigała and others, 1988; Reference Kohler, Moore, Kennett, Engeset and ElvehøyKohler and others, 1997; Reference Winther, Bruland, Sand, Killingtveit and MarechalWinther and others, 1998, Reference Winther2003). The variability of snow accumulation has rarely been compared to recorded precipitation at weather stations, due to weak statistical relations between such elements. According to Reference Hagen and LiestølHagen and Liestøl (1990), the correlation coefficient between snow accumulation of austre Brøggerbreen and the sum of winter precipitation at Ny-Ålesund station, located in the immediate vicinity of the glacier, was only 0.63. Errors in precipitation measurements are one possible reason for such weak correlation between actual mass accumulation and recorded precipitation. Errors in precipitation measurements cause the true precipitation to be overestimated by about 50% a-1 compared with measurements from the Ny-Ålesund station (Reference Hanssen-Bauer, Førland and NordliHanssen-Bauer and others, 1996; Reference Førland and Hanssen-BauerFørland and Hanssen-Bauer, 2000). Measurement errors become more severe with increasing wind strength and with decreasing temperature.
The Algorithm of Accumulation Assessment
Algorithm description
To assess the amount of accumulation at any point on a Svalbard glacier, I used the following equation:

where acc( l ,hi ) is snow accumulation (mmw.e.) on a glacier situated at a distance l from the open water at a point located at a height of hi ; Bh0 is winter accumulation (mmw.e.) at a reference station at altitude h0; Lc is the location coefficient; and τ is the accumulation gradient, i.e. the relative accumulation increase per 100 m (%).
The distance from open water is measured in a straight line between a weather station (l) or point located in the center of the glacier equilibrium line (d) and the nearest point on the coast of the open sea. Coasts composed of fjords, small bays and straits are not used to calculate distance.
B h 0 is estimated on the basis of the sum of winter precipitation measured at the weather station and may be calculated by:
where Ph 0 is winter (October-May) precipitation (mm) at a reference station at altitude h0, and K is the efficient accumulation correction coefficient.
The efficient accumulation correction coefficient K calculates seasonal accumulation rates from the total winter precipitation. The value of K is affected by two factors: error in precipitation measurements, which increases K, and the effect of rain, which decreases K. It is important to consider rain because not all winter precipitation is actually accumulated. Rain episodes included in total winter precipitation do not influence accumulation increase. Consequently, it could be assumed that accumulation is equal to the sum of real solid precipitation. K can be expressed as
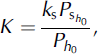
where k s is the correction factor for solid precipitation assumed to be equal to 1.85 as suggested by Reference Førland and Hanssen-BauerFørland and Hanssen-Bauer (2000), and P sh0 is winter (October–May) solid precipitation (mm) at a reference station at altitude h 0.
The K coefficient is a function of solid precipitation rate in the total winter precipitation and may range from 0 to 1.85. If only winter precipitation data with no distinction of types are available, K is assumed to be equal to 1.1. This value of K is valid when 60% of measured precipitation occurred as snowfall. This value is the average solid precipitation rate in the winter seasons 1975–96 at Ny-Ålesund (Reference Førland and Hanssen-BauerFørland and Hanssen-Bauer, 2000).
Precipitation is characterized as a factor of great spatial variability, due mainly to surface topography and orography. In order to determine spatial regularities in the winter precipitation distribution, the sums of precipitation at weather stations have been compared with their distances from open water. Most weather stations are located along the coast at low elevation. This allows us to assume that most weather-station data were collected at sea level. Differences in precipitation at particular stations are a function of continental influence, so the further a station is situated from open water, the lower the precipitation. Table 1 shows mean values of the sums of precipitation from October to May from the normal period 1961–90 for six Spitsbergen stations (Ny-Ålesund, Isfjord Radio, Svalbard Lufthavn, Longyearbyen, Sveagruva and Hornsund). The locations of weather-stations are shown in Figure 1. The average values of precipitation show a strong relation with distance from open water (Fig. 2). Regression analysis of the data in Table 1 made it possible to describe the long-term average of winter precipitation at Spitsbergen stations (p w, given in mm) as a function of distance from open water (l, given in km):
Table 1. Mean values of sums of winter precipitation (October– May) from the normal period 1961–90 for the Spitsbergen stations (Reference Førland, Hanssen-Bauer and NordliFørland and others 1997), the distance to the open sea, and converting equations of location coefficient (L c)
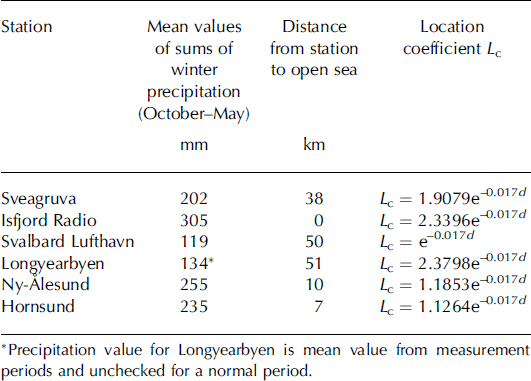
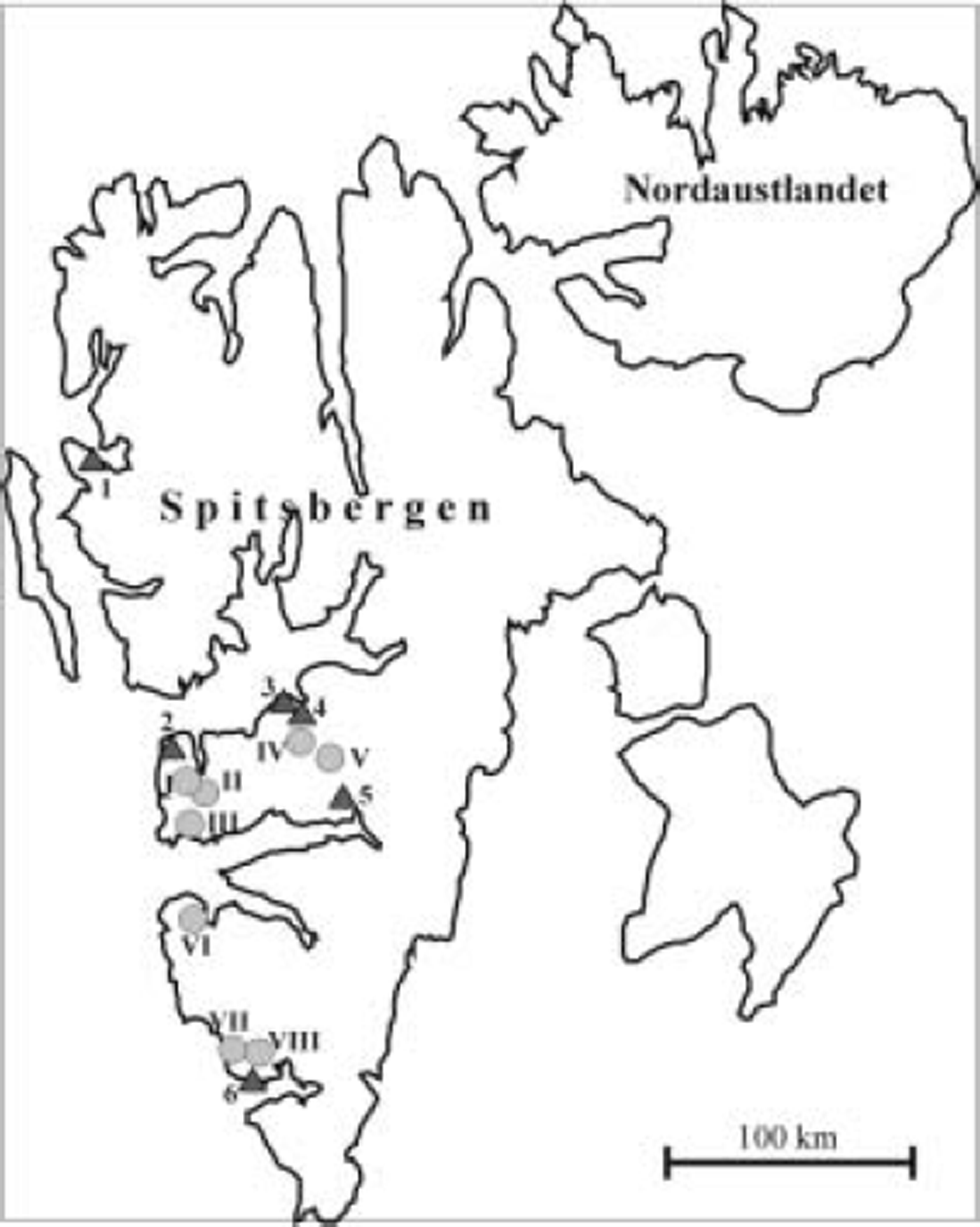
Fig. 1. Locations of weather stations at Svalbard (triangles) and glaciers (filled circles) for which the assessment of accumulation was done: 1. Ny-Ålesund; 2. Isfjord Radio; 3. Svalbard Lufthavn; 4. Longyearbyen; 5. Sveagruva; 6. Hornsund. I. Vestre Grønfjordbreen; II. Austre Grønfjordbreen; III. Fridtjovbreen; IV. Bogerbreen; V. Gløtfjellbreen; VI. Renardbreen; VII. Werenskioldbreen; VIII. Hansbreen.
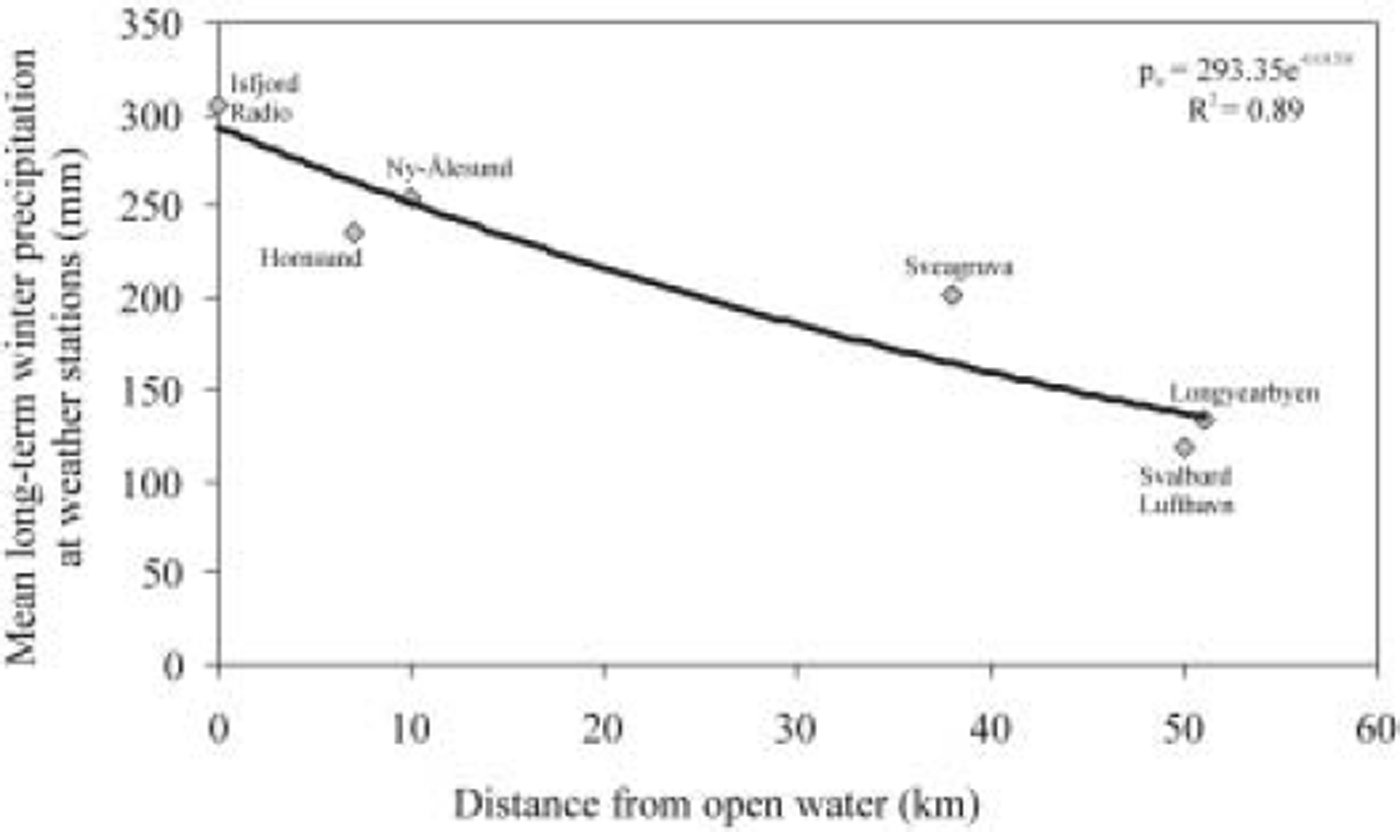
Fig. 2. Relations of mean precipitation in the winter seasons 1961– 90 in a normal period at Spitsbergen stations with the distance to the open sea.
This equation explains 89% of the variation in mean winter precipitation on western and southern Spitsbergen. For the following calculations I assume that the above relationship is valid for each winter season.
The location coefficient describes the relation between the sum of winter precipitation at a site located at a given distance from the open water and precipitation at a particular station. On the basis of Equation (4), the location coefficient Lc has been calculated:
where d is the distance between a glacier’s equilibrium line and the open water.
The coefficient Lc has been calculated for every weather station separately. Using the conversion formula, the sum of winter precipitation will be greater at points nearer to the sea and smaller at points farther inland in comparison with sums recorded at the reference station. With a view to limiting potential errors in further accumulation assessments, meteorological points closest to the analyzed glacier have been used as reference stations.
The value of sea-level accumulation obtained using the above calculation is then converted into accumulation at a given altitude of measurement point, according to the applied accumulation gradient r. This gradient is defined as the increase in percentage of accumulation at sea level per 100m of elevation change. This is a simplification that assumes accumulation variability is due only to changes in absolute altitude and that ignores the influence of topographic factors and possible inversion of precipitation. Elevation above sea level, however, is the most important factor for determining the accumulation variability on glaciers, hence the obtained value assumed to be used as the mean snow accumulation at a given altitude. The accumulation gradient is not a constant value but increases proportionally with increasing accumulation at sea level. In this study, the accumulation gradient 0.4–0.8 has been tested and appears to be valid.
Analysis of error assessment
The measured accumulation was compared with elevation using a regression. The regression line shows a good approximation of normal accumulation conditions over the elevation profile. As a test of accumulation assessment, I compared the regression line with the results of calculations.
Over the examined elevation ranges, I established mean deviations from the regression line S using the following method:
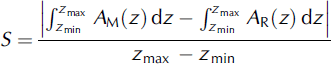
when functions AM(z) and A R(z) do not intersect in the range ( z min; zmax), and
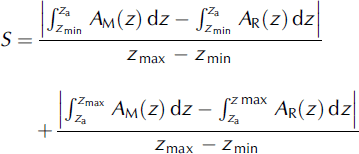
when functions AM(z) and AR(z) intersect in the range (z min; zmax), where AM(z) is the linear function of evaluated accumulation vs elevation above sea level, AR(z) is the linear function, i.e the regression line of the measured accumulation vs elevation above sea level; z min is the altitude (ma.s.l.) of the lowest accumulation measurement point located on a glacier; z max is the altitude (ma.s.l.) of the highest accumulation measurement point located on a glacier; and z a is the altitude (ma.s.l.) of intersection of functions AM(z) and AR(z).
For an easier comparison of errors of various glaciers and seasons, deviations have been converted into percentage values, where 100% stands for the mean measured accumulation in examined elevation profile (A s) of a given glacier:
Results
The algorithm of accumulation assessment has been applied to eight glaciers for which snow accumulation data over the full range of glacier elevation are known. The data are valid mainly for points located along the central axes of these glaciers. The glaciers are as follows: Hansbreen, Werenskioldbreen and Renardbreen in southern Spitsbergen; Fridtjovbreen, austre and vestre Grønfjordbreen on the west coast; and Bogerbreen and Gløttfjellbreen located in the centre of the island (Fig. 1). For glaciers in the central and western part of Svalbard, data exist for the years 1966 and 1967 (Reference Mikhaliov and SingerMikhaliov and Singer, 1975). For Renardbreen, data are available for 1987 (Reference Piasecki, Jahn, Pereyma and Szczepankiewicz-SmyrkaPiasecki, 1988). For Werenskioldbreen, data are available for 1994 (Reference JaniaJania, 1994) and 1999–2002 (P. Głowacki, unpublished data). For Hansbreen, data are available for 1989–99 (P. Głowacki, unpublished data) (Table 2). In total, 23 seasons of accumulation data for the glaciers were analyzed.
Table 2. Precipitation data and location of glaciers selected for verification of the accumulation model. Reference stations: Isfjord Radio*; Hornsund†; Svalbard Lufthavn‡
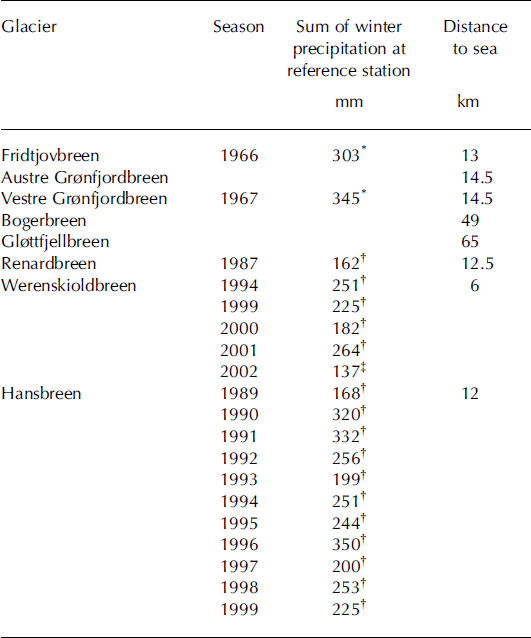
Isfjord Radio was used as the reference station for defining accumulation on glaciers of central and western Spitsbergen. For the southern region, Hornsund station was used, except for the 2001/02 season when, due to the lack of data, meteorological observations from Svalbard Lufthavn were used instead (Table 2).
Snow accumulation assessment based on precipitation data with no distinction of precipitation types
When only the sum of winter precipitation at weather stations is available, the efficiency accumulation correction coefficient K is assumed to be a constant value equal to 1.1. The snow accumulation was estimated using the accumulation gradient τ in a range 0.4-0.8 (Table 3). The lowest error of accumulation assessment was obtained with the application of τ = 0.6. The mean error of accumulation estimation for analyzed glaciers in that case amounted to 23%. Average errors range between 4% (Werenskioldbreen 2002) and 43% (Hansbreen 1989), with a median value of 16% (Table 4). The full results of accumulation estimation are presented in Figures 3-6.
Table 3. Maximum and mean errors of snow accumulation assessment for defined coefficients of precipitation correction (ka) and precipitation gradient (τ The smallest values of errors are in bold
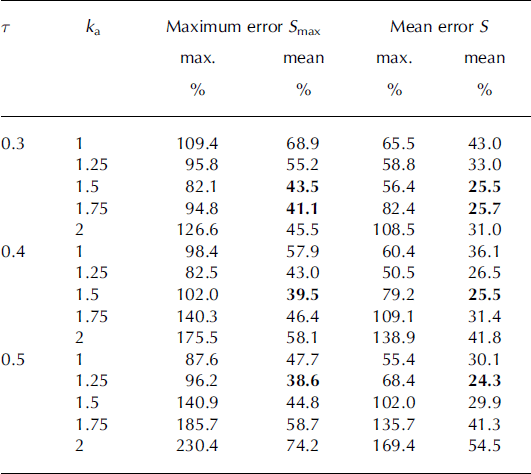
Table 4. Values of coefficients ka and τ assuming optimum accumulation assessment. The best-matched values of coefficients in each investigated season are in bold

Fig. 3. Observed and modeled values of accumulation on Fridtjovbreen, austre Grønfjordbreen, vestre Grønfjordbreen, Bogerbreen and Gløtfjellbreen in the years 1966-67.

Fig. 4. Observed and modeled values of accumulation on Werenskioldbreen in 1994 and 1999–2000 and Renardbreen in 1987.
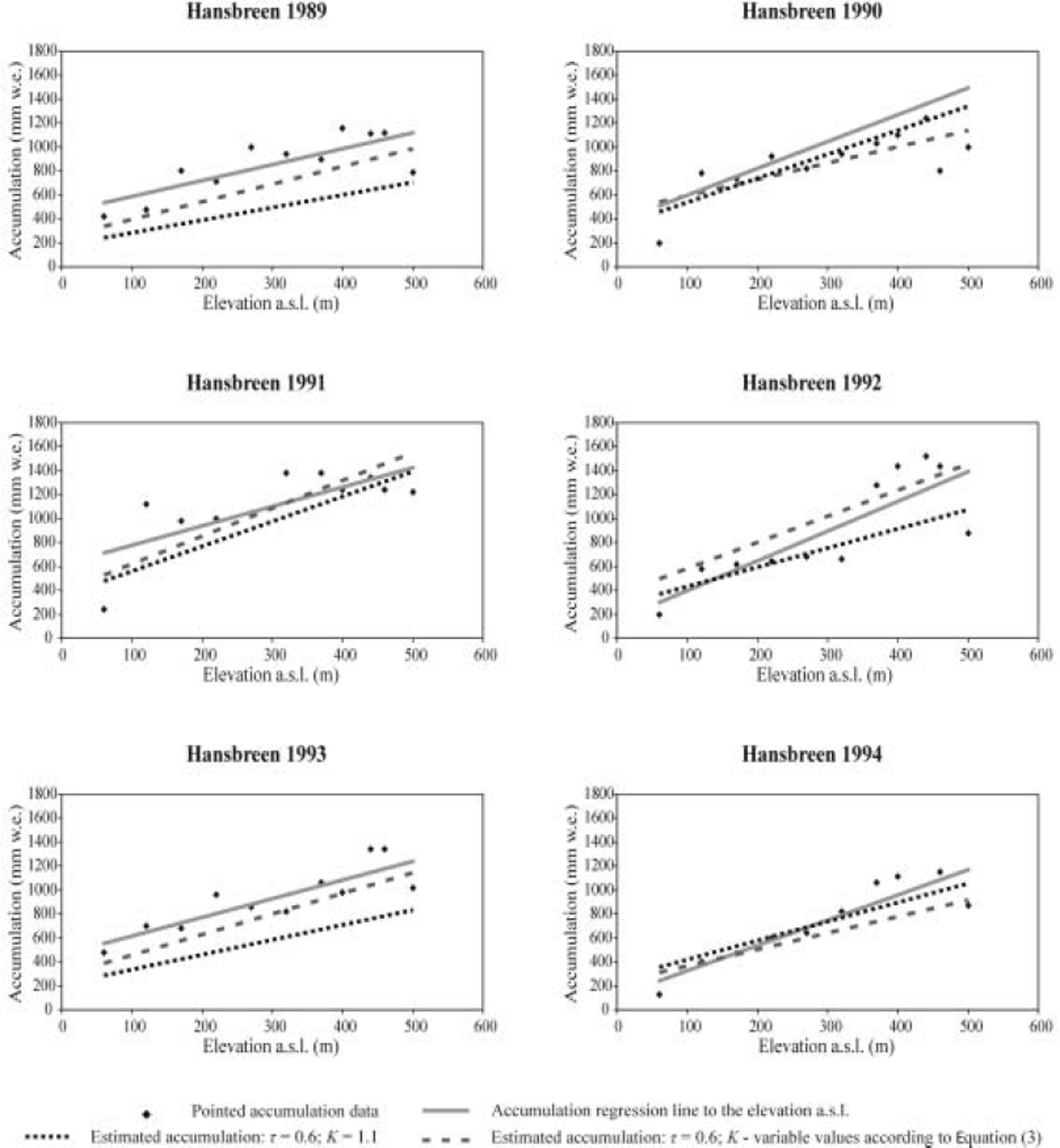
Fig. 5. Observed and modeled values of accumulation on Hansbreen in the years 1989–94.
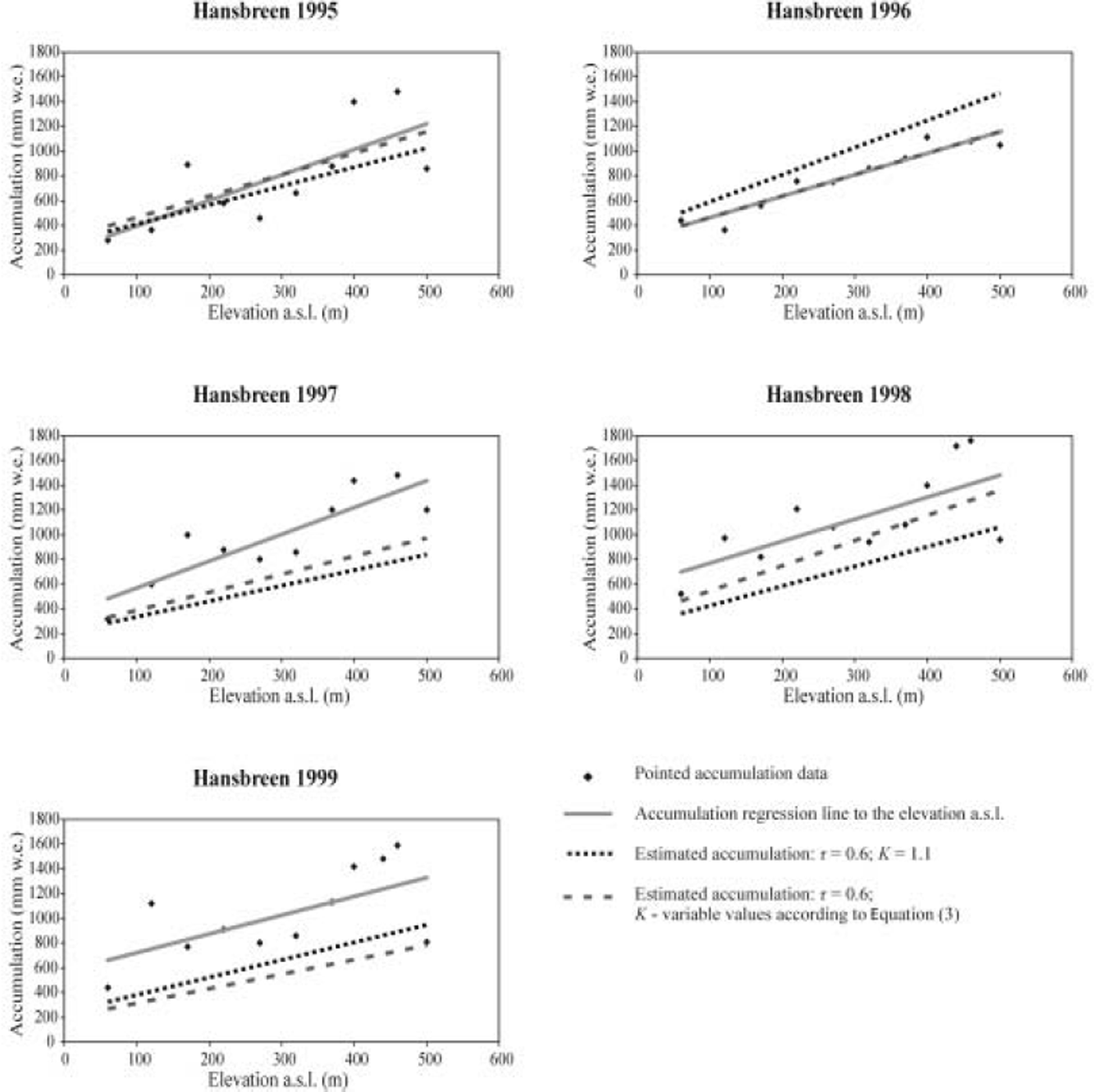
Fig. 6. Observed and modeled values of accumulation on Hansbreen in the years 1995–99.
Snow accumulation assessment based on precipitation data with distinction of precipitation types
The procedure presented below has been applied only to glaciers on southern Spitsbergen (Hansbreen, Werenskioldbreen and Reanardbreen) where it is possible to distinguish solid precipitation using data from Hornsund station. I assumed that all precipitation on days with an average temperature ≤0.5°C was snow (after Reference Førland and Hanssen-BauerFørland and Hanssen-Bauer, 2000). I used an accumulation gradient of τ = 0.6, which was determined as outlined above. The results of the accumulation assessment and the errors are presented in Table 4 and Figures 4-6. Using this method, the mean error of the accumulation estimation for the glaciers is 7% lower than the results of assessment using the sum of winter precipitation only.
Discussion
The processes that lead to variations in snow accumulation over glacier surfaces are one of the reasons for the accumulation assessment errors. The algorithm does not explain variations in accumulation related to, for example, glacier topography, orography of the surroundings, snowdrift and precipitation inversion. These influences have a noticeable effect in the upper part of Hansbreen. In many seasons, the snow accumulation measured at 500ma.s.l. was substantially smaller than that measured at a stake located ∼50 m lower. Hansbreen also has an asymmetric accumulation distribution, with greater accumulation on the western side of the glacier than on the eastern side (Reference JaniaJania, 1994). This pattern is common on glaciers oriented perpendicular to prevailing winds (e.g. Bogerbreen and Bertilbreen; cf. Reference Gus’kovGus’kov, 1983; Reference Gus’kov and TroitskiyGus’kov and Troitskiy, 1984, Reference Gus’kov and Troitskiy1985, Reference Gus’kov and Troitskiy1987). This leads to significant differences in accumulation across the glacier at the same altitude.
The errors of estimation could also be caused by micro-relief of the glacier’s surface that contributes to snow accumulation (concave forms) or erosion (convex forms). Intensive redistribution of blowing snow out of the convex form has been observed on land-based glaciers fronts (e.g. Werenskioldbreen). In such cases, the algorithm will overestimate accumulation.
Other sources of error arise from approximations and assumptions. For the calculation of the location coefficient L c, the glacier has been considered as a point object. As a result of this simplification, the distance from open water has been measured between a point located in the center of the glacier equilibrium line and the nearest point on the coast of the open sea. This could cause substantial errors where glaciers extend long distances from the sea coast towards the center of the island. One may consider a hypothetical glacier terminating in the open sea, the most distant point of which is located 20km from the open water. The difference in the sum of winter accumulation at sea level between those two extreme points of the glacier, calculated on the basis of Equation (4), amounts to 26.4%. Applying the constant distance to the open water for every point on the glacier’s surface, the accumulation on sites located nearest to the sea is underestimated, whereas the accumulation at the most distant points is overestimated.
The accuracy of the efficient accumulation correction coefficient (K) is determined by the quality of precipitation data. The K coefficient is dependent upon the solid precipitation rate in relation to the total winter precipitation. If there are no data on precipitation type, any approximation (e.g. use of temperature criterion or constant solid precipitation rate) would be a source of error. Additionally, the correction factor for solid precipitation (ks) gives only a rough approximation of the true value of precipitation.
The observed accumulation gradients τ are not constant in space and time as has been assumed in this study. The τ factor on Hansbreen in the years 1989-99 ranged from 0.41 to 1.04. The differences between the τ value applied in the accumulation assessment (τ = 0.6) and the observed accumulation gradient could result from snow distribution disturbances on glaciers discussed above.
Conclusions
The results show a simple way to estimate accumulation for any point on Spitsbergen glaciers. The proposed evaluation procedure is mainly intended for use on western and central Spitsbergen. This is because insufficient meteorological data are available from the eastern part of the island and because of difficulties in verifying the accumulation approximation on glaciers of eastern Spitsbergen.
The minimum requirements for the accumulation estimation are the sum of winter precipitation at the nearest weather station and the location of the analyzed site on a glacier, i.e. distance from open water and elevation. The results of accumulation assessment are closer to actual values when the sum and rate of solid precipitation have been applied. Precipitation type is the most important factor determining snow accumulation.
The application of the presented algorithm allows for calculation of the accumulation on glaciers of central and southern Spitsbergen with an accuracy of 19–23%. The errors result from the exclusion of factors disturbing accumulation distribution in the elevation profile (e.g. glacier topography, orography of the surroundings, precipitation inversion) as well as assumptions and approximations. The focus of future work will be centered on the reduction of errors.
The application of my accumulation algorithm may provide a crucial element of mass-balance evaluation for glaciers not included in permanent monitoring.
Acknowledgements
I thank J. Jania for inspiring me to take up this topic. I also thank P. Głowacki (Polish Academy of Sciences) for making available mass-balance data of Hansbreen and meteorological data from Hornsund station, and I. Hanssen-Bauer and an anonymous reviewer for valuable comments on the manuscript. A. Lewis and K. Tomala kindly corrected the English. This research was supported by the Committee of Scientific Research, Poland (KBN) under grant No. 6 P04E 00821.












