Climatic controls of glacier distribution and glacier changes in Austria

Abstract

In this study we aim to connect glacier extent in 1998 with general climatic conditions, and glacier changes between 1969 and 1998 with climate change in the Austrian Alps. The investigations are based on two complete glacier inventories, a homogenized gridded precipitation dataset and European Centre for Medium-Range Weather Forecasts re-analysis (ERA-40) data of air temperature at different levels. A relationship between median glacier elevation, minimal elevation, the general elevation of the surrounding mountains and mean climatic values was found. In the Austrian Alps, the existence of glaciers at low elevations can only be maintained with above-average accumulation or strong dynamic ice supply. For debris-free glaciers, we found a limit of ~2080ma.s.l., where mean summer temperatures (June–August) exceed 4°C. Glacier changes from 1969 to 1998 are strongly negative both in relative area and in mean thickness. There is a weak and regionally varying negative trend in precipitation over this period. A spatially consistent sequence of positive temperature anomalies in the early 1980s and after 1990 offers an explanation for the retreat. The study shows that the observed spatial variability of glacier changes is connected more strongly to the topographic differences than to a regionally different climate change signal.

Introduction

The extent and location of mountain glaciers depend on both topography and climatic conditions. These two factors are interdependent because of the altitudinal gradients in temperature and precipitation but also as a result of synoptic processes (e.g. prevailing weather patterns, orographic uplifting) and specific local factors (e.g. local snow distribution, avalanching, shading). Furthermore, glaciers transport ice from high elevations to the terminus such that in steady-state conditions, low-elevation melt equals dynamic resupply. Thus, conditions that affect the upper end of a glacier (i.e. above-average precipitation) also help determine the altitude of its lower end (i.e. below-average elevation of the glacier tongue). The combination of regional glacier inventories taken at different points in time with climate data provides an opportunity to study the connection between glacier distribution, glacier change and climate.

Attempts to understand this complex combination of factors have been made by Shea and others (2004) for the Canadian Rockies and by Schiefer and Menounos (2010) for British Columbia, Canada. The relationship between exposure to solar radiation and glacier distribution was investigated by Evans and Cox (2005) for glaciers worldwide, in greater detail by Evans (2006) for alpine glaciers, and by Evans and Cox (2010) for arctic glaciers only. Haeberli and Hoelzle (1995) relate inventory data to basic glaciological characteristics in the European Alps; Hoelzle and others (2007) derive estimates of surface mass balances from glacier inventories and a parameterization scheme comparing the European Alps with the Southern Alps of New Zealand. Recently, the glacier setting in northern Italy (Knoll and others, 2009) has been described comprehensively and Bolch and others (2010) investigate regionally different glacier changes in western Canada based on Landsat scenes. This dataset is also used in various publications on glacier changes in the Swiss Alps (e.g. Kääb and others, 2002).

In this study the Austrian glacier inventories (Patzelt, 1980; Gross, 1987; Lambrecht and Kuhn, 2007; Kuhn and others, 2009a), which are unique in both accuracy and timespan, are used to investigate the relationship between: (1) glacier location and representative climatic parameters; and (2) glacier changes as a direct result of climate change.

Study Area

The investigations are performed in the Austrian part of the eastern Alps (46˚40′–47˚35′ N, 9˚50′–13˚40′ E) where, in 1998, 910 glaciers covered a total area of 470 km² (Lambrecht and Kuhn, 2007). Figure 1 shows a map with the 1998 glacier coverage and an Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) digital elevation model (DEM) of elevations higher than 2000m a.s.l. in the background. The ASTER DEM is for illustrative purposes; the analyses carried out in this study were performed with photogrammetrically derived DEMs. The largest part of the glacial area is along the main alpine divide, which follows the southern border of Austria from approximately 10˚30′ E to 12˚15′ E and continues eastward into the Austrian interior. Some small glaciers exist along the northern slopes of the Alps where peak altitudes are significantly lower. The ellipses indicate glacier groups of fairly uniform climatic and topographic settings (A–E in Fig. 1).

Fig. 1. Glacier cover in Austria according to the glacier inventory of 1998 (black outlines; Lambrecht and Kuhn, 2007) and an ASTER DEM in the background displaying elevations higher than 2000ma.s.l. in colour. This figure distinguishes five areas (A–E) by their climatic and topographic settings. Austria’s two largest glaciers, Pasterzenkees (PAS) and the Gepatschferner (GEP), are labelled.

Data and Methods

Two complete glacier inventories compiled in 1969 (Patzelt, 1980; Gross, 1987) and 1998 (Lambrecht and Kuhn, 2007; Kuhn and others, 2009a) are used in this study. Both surveys were conducted by aerial photogrammetry and include glacier boundaries as well as DEMs. Median elevations were calculated from the DEMs by linearly interpolating the area–elevation distribution, given in 50 m elevation bands, to the elevation where 50% of the individual glacier’s area is located above and 50% below. The median elevation is a characteristic glacier variable as shown by Kuhn and others (2009b) who use the median elevation to transfer mass-balance profiles from measured to unmeasured glaciers.

Mean glacier thickness changes, Δz, have been calculated as follows, where the overall volume change between 1969 and 1998 is ΔV _1969–98 and the glacier areas in 1969 and 1998 are A ₁₉₆₉ and A ₁₉₉₈:

(1)

Estimates of the accuracy of area and volume changes are made by Gross (1987), Eder and others (2000) and Lambrecht and Kuhn (2007).

We were interested in calculating a single temperature variable and single precipitation variable for each glacier that would best represent the local climate. As glacier mass balance in the Alps is influenced most strongly by summer temperature and winter precipitation (e.g. Kuhn and others, 1999), these two quantities were derived as a basis for comparisons.

The mean summer temperature was defined as the temperatures averaged between June and August inclusive. The temperature data were obtained from the European Centre for Medium-Range Weather Forecasts re-analysis project (ERA-40) (Uppala and others, 2005), which includes a dynamically consistent three-dimensional gridded dataset combining a numerical weather forecast model, meteorological observations and data from satellites from 1957 to 2002. The gridspace of the ERA-40 data is 1.25˚. As temperature is highly elevation-dependent and thus a sensitive parameter when comparing glaciers of different sizes in different regions (with different altitudes as a consequence) a glacier-relevant constant level of 2500m a.s.l. was defined. This is a typical elevation of high summer ablation areas in the Alps (e.g. WGMS, 2008) and always falls between the ERA-40 pressure levels of 700 and 850 hPa. Six-hour temperatures and the respective geopotential for these levels at the ERA-40 gridpoints were used. These values then were interpolated to derive time- and space-dependent lapse rates of temperature. Using the temperature and elevation of the 700 hPa pressure level together with the derived lapse rates, the mean summer temperature at 2500 ma.s.l. was determined.

Efthymiadis and others (2006) created a precipitation dataset with monthly resolution and 10 0-sized cells for the entire Alps by homogenizing weather station data from more than 150 stations. Winter precipitation was determined for each glacier by interpolating linearly between the respective gridpoints and summing monthly precipitation values between October and May inclusive. The precipitation dataset is created using valley stations only (stations below 1900 m; Auer and others, 2005) because of the notorious uncertainties of high-altitude precipitation measurements (e.g. Yang and others, 1998; Sevruk, 2004). As precipitation has a higher local (x, y, z) variance than temperature, the precipitation field used in this study is less accurate than the temperature field.

Both winter precipitation and summer temperatures have been averaged to find the widespread ‘climatological mean’ of 1961–90 and are referred to as mean winter precipitation and mean summer temperature. The ‘climatological mean’ was chosen in order to make our results comparable with other studies; however, as we are concerned only with how these data change qualitatively over time (i.e. anomalies), the use of a different period would not alter the results of the study but would instead shift the curves along the ordinate.

To analyse temporal changes in winter precipitation and summer temperature the cumulative anomalies of these variables were derived from the climatological mean from 1969 to 1998, the years in which the two glacier inventories were compiled.

Results

Glacier distribution and climatic setting

Figure 2a displays the relationship between mean winter precipitation over the period 1961–90 and median glacier elevation from the inventory of 1998. Mean winter precipitation varies considerably in the Austrian Alps: the wettest areas receive nearly three times as much precipitation as the driest. The drier the local climate, the earlier a glacier exposes bare ice at a given altitude and the longer the ablation period lasts. As a result, for a given altitude and during a period of general warming, glaciers situated in a drier climate are expected to lose more mass than glaciers situated in a wetter climate.

Fig. 2. (a) Mean winter precipitation (1961–90) in the study area (background) and each glacier’s median elevation (circles). Precipitation data from Efthymiadis and others (2006). (b) Mean summer temperature (1961–90) at 2500ma.s.l. derived from ERA-40 data (background) and each glacier’s minimum elevation (circles).

Mean winter precipitation is greatest in the easternmost and westernmost parts of Austria’s glacial region and much lower in the centre. Glaciers in the north and northeast tend to be fairly wet as well. This pattern is readily explained by the fact that most winter precipitation falls out of weather systems from the north and northwest (Fliri, 1975). The inner alpine areas are shielded from the bulk of these systems by the northern ridges. The eastern ridges are less thoroughly shielded as the northern alpine ridge is more open there.

In general, the pattern of median elevations closely follows the pattern of winter precipitation. Wetter glaciers in the west and east have lower median elevations (e.g. 2500ma.s.l. in the northwest), while glaciers in the dry Ötztal and Stubai region are typically much higher (~3000ma.s.l.) (Kuhn and others, 2009b).

Temperature is highly elevation-dependent and thus the median elevation contains a simplified temperature signal. In turn, the median elevation of a glacier can be expected to be influenced by temperature conditions. To study the horizontal temperature signal, the mean summer temperature at 2500 ma.s.l. as derived from the ERA-40 is presented in Figure 2b. Summer temperatures at 2500 ma.s.l. average 5.5˚C, with variations of <0.5˚C in either direction. There is a north-to-south temperature gradient, with higher temperatures in the south.

For various size classes, the lowest altitude of each glacier in 1998 is related to mean winter precipitation and mean summer temperature at 2500 ma.s.l. in Figure 3. Each circle represents one glacier; the size of each circle is proportional to the area of the respective glacier. In each figure the correlation coefficient, r, between minimum elevations and mean winter precipitation is displayed. Correlations in Figure 3a–e are statistically significant at the 99% confidence level; the correlation in Figure 3f is statistically significant at the 95% confidence level. The relation between the parameters mentioned is investigated for all glaciers in Figure 3a and for individual size classes in Figure 3b–f.

Relationships exist between:

minimum elevation and mean winter precipitation. Figure 3a–f show generally higher values of minimum elevation in regions with less winter precipitation, resulting in negative slopes of the regressions. This supports our hypothesis that greater accumulation leads to more mass turnover and lower minimum elevations.

minimum elevation and mean summer temperature at 2500ma.s.l. (Fig. 3, colour code). Areas with higher minimal elevations coincide with slightly higher temperatures than areas with lower minimum elevations. These also generally coincide with drier regions (compare with Fig. 2a and b).

Fig. 3. Mean winter precipitation vs a glacier’s minimum elevation, each point representing one glacier’s climatic conditions. The size of the circles is proportional to the glacier’s area and the colour code is a measure for the mean summer temperatures at 2500ma.s.l. at the glacier’s position. (a) All glaciers; (b–f) glaciers are divided into area classes.

minimum elevation and glacier area. In general, the larger the glacier, the lower the minimum elevation; this is due to larger mass turnover for large glaciers than for small glaciers. Note the progression of the cluster of dots from high (Fig. 3b) to low (Fig. 3f). For comparisons of glacier changes across different regions it is therefore advisable to compare glaciers of similar area only.

To quantify the relations described above objectively, a multiple regression was run, where the minimum elevation is z _min (m), the mean winter precipitation for 1969–90 is p _w (m), the mean summer temperature at 2500 ma.s.l. is T _s2500

(K) and the glacier area in 1998 is A ₁₉₉₈ (m²):

(2)

The correlation coefficient between predicted and measured minimum elevations is 0.65. Logarithmic or square-root transformations were selected by evaluating different possibilities and choosing the best result (highest correlation coefficient). A similar regression analysis was performed with median elevations, but that leads to a weaker correlation (r = 0.55).

Glacier changes

In order to interpret the relationship between regional climate and resulting glacier changes, the spatial distributions of relative area changes and mean thickness changes between the glacier inventories of 1969 and 1998 are displayed in Figure 4. The overall results for the defined regions A–E are summarized in Table 1, wherein relative area changes and mean thickness changes of the regions are subdivided into glaciers smaller than 0.5 km² and glaciers larger than 0.5 km²; the total values are shown in the last two columns. Small glaciers generally shrank more in area and less in mean thickness than large glaciers. Regions A and E, the two regions situated furthest north in the study area, show less negative area changes than the more central alpine regions B, C and D, the only exception being relative area changes of glaciers larger than 0.5 km² in region A. With the same exception, changes within regions B and C are significantly more negative than within A and E. Reductions in area and mean thickness are of similar magnitude throughout regions B and C. Region D contains Austria’s largest glacier, Pasterzenkees, which influences the negative record value for mean thickness changes of glaciers larger than 0.5 km² and is also visible in the negative record of mean thickness change values for all glaciers.

Fig. 4. (a) Relative area changes and (b) mean thickness changes between 1969 and 1998. The crosses display glacier coordinates of glaciers that are smaller than 0.5 km². The ellipses A–E show areas referred to in the text.

Table 1. Summary of relative area and mean thickness change for glaciers smaller than 0.5 km², glaciers larger than 0.5 km² and all glaciers in the areas shown in Figure 1 and the values for all glaciers in total

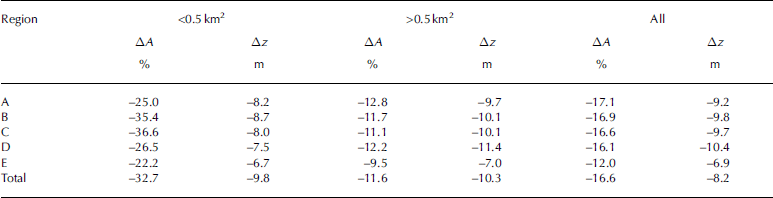
Small glaciers are strongly influenced by very local conditions such as wind, avalanches or topographic shading (e.g. Kuhn, 1995; DeBeer and Sharp, 2009). This makes it very difficult to interpret changes in the size or thickness of small glaciers as a direct result of climate change. In order to keep Figure 4a and b more comprehensible, changes of glaciers larger than 0.5 km² are displayed in colour; smaller glaciers are plotted as black crosses. Both relative area changes and mean thickness changes show a very heterogeneous pattern between the regions, as pointed out above and quantified in Table 1, but also contain gradients within the regions.

The westernmost glacier in region A shows a more negative value than the others in region A; however, the change in one rather small glacier should not be over-interpreted. More significantly, region B has a wide variety of values with a north-to-south gradient, which is visible both in relative area changes (Fig. 4a) and mean thickness change (Fig. 4b). At the southern edge of B, along the main alpine divide, glaciers shrank more and lost more of the initial thickness than in the north. Within region C, area changes tend to be less negative in the eastern part than in the western part; this is only barely visible in mean thickness changes. With the exception mentioned above, region D generally displays slightly less negative values than those in region E, where the western part (Hochköniggruppe) experienced significant area loss (approximately –20%). The eastern part (Dachstein) of region D changed little.

The pattern of mean thickness changes (Fig. 4b) is weakly but significantly related to the pattern of relative area changes, with a correlation coefficient of 0.29 at the 99% confidence level.

Climate change

In Figure 5, glacier area and volume changes are related to possible regional differences in climate change. Figure 5a displays the cumulative anomalies of winter precipitation from the long-term winter precipitation mean (1961–90) for the center of each region (Fig. 1). There is no significant overall trend of winter precipitation in regions A, B and E. Following a slightly negative precipitation anomaly in the early 1970s, eastern areas (D, E) show basically no trend from that date forward with the exception of a few years with positive anomalies in the early 1980s. In regions C and D, however, the study period also started with some negative anomalies (until the mid-1970s), followed by basically no anomalies until about 1985. After that, a series of years with stronger negative anomalies occurred again.

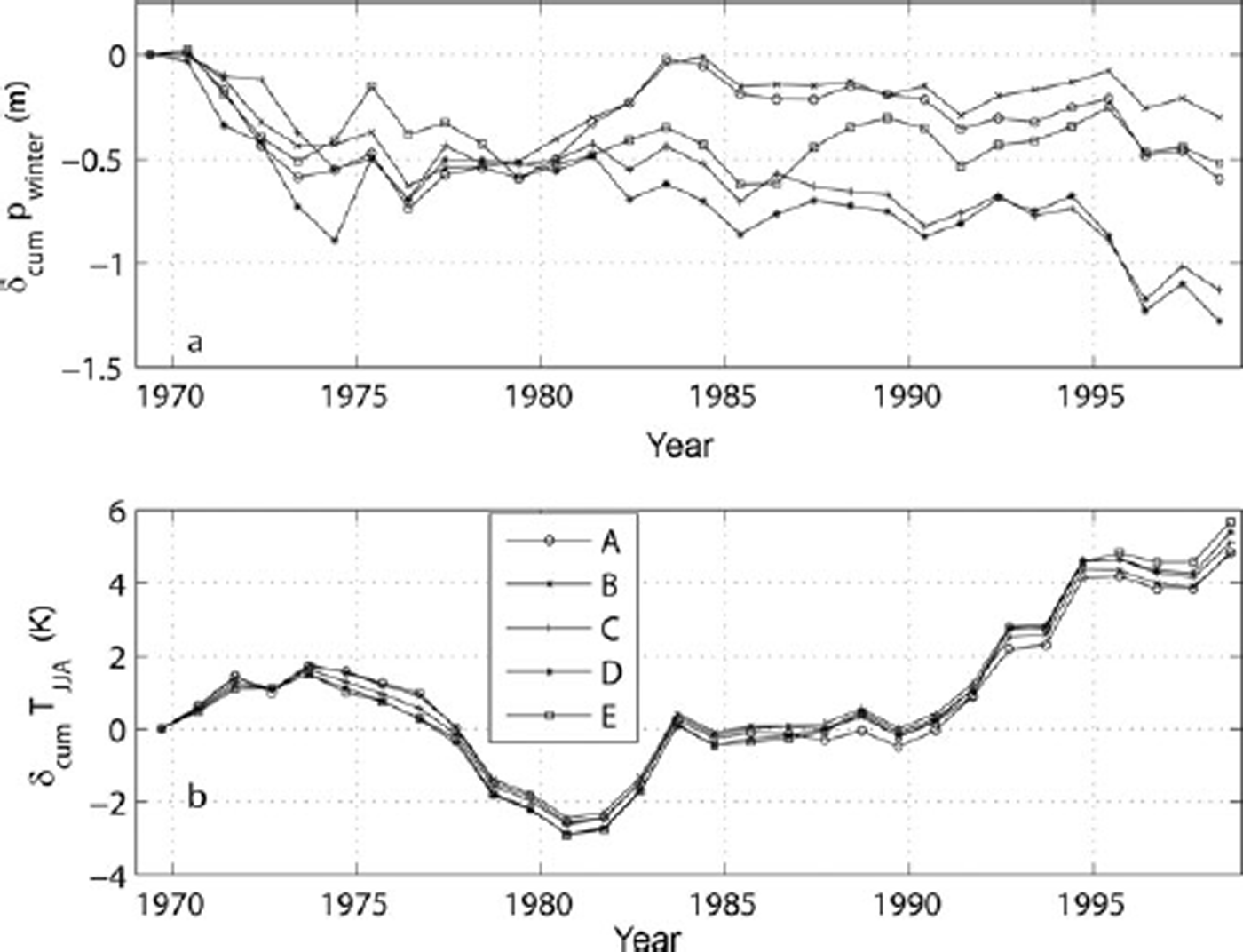
Fig. 5. Cumulative anomalies from the climatological mean (1961–90) at the centre of regions A–E (see Fig. 1). (a) Cumulative anomalies of winter precipitation and (b) cumulative summer temperature anomalies at 2500ma.s.l.

Temperature anomalies (Fig. 5b) show less spatial variability than do precipitation anomalies. There are six distinct time periods: an initial positive anomaly (1969–73); generally negative anomalies (1974–80); strong positive anomalies (1981–83); temperatures near the mean (1984–89); strong positive anomalies (1990–95); until 1998 nearly average ones. Both positive and negative temperature anomalies were strongest in region E and weakest in region A. There are no significant negative summer temperature anomalies after 1981.

Discussion

The results presented above attempt to relate climatic parameters to typical descriptive glacier variables. We propose to invert this argument by asking: which climatic parameters are necessary to establish an environment in which a typical glacier can exist? While there are exceptions like Boggeneikees, which survives 5˚C summer temperatures at <1750ma.s.l. due to debris cover and a reliable ice supply through a steep narrow valley, glacier size is the dominant parameter that determines the minimum elevation (Fig. 3), suggesting that ice dynamics plays the most important role. The glacier size signal thus has to be removed in order to determine the effects of different climatic parameters on the minimum elevation; this is accomplished by comparing glaciers of similar size. The two largest glaciers, Pasterzenkees and the Gepatschferner (for locations see Fig. 1), have their minimum elevations at about the same altitude, ~2080 m, despite very different precipitation conditions because of compensating differences in their respective topographic settings. The Gepatschferner has a larger accumulation-area ratio than Pasterzenkees because of larger portions of the glacier at high elevations. Therefore less accumulation is necessary in order to transport mass to similarly low elevations. The lowest elevation of these glaciers (2080 m) can be taken as the limit at which debris-free glaciers can exist in the study area. Smaller glaciers show a significant dependence of minimum elevations on mean winter precipitation (Fig. 3b–f).

While the sign of the correlation coefficient (negative in all correlations; Fig. 3a–f) demonstrates a dependence of minimum elevation on mean winter precipitation, the upper boundary of the point cloud, that is the highest elevation of the terminus for a given precipitation value, must be interpreted differently because the peak elevations of the glacier-covered areas vary widely within the study area.

The correlations shown in Figure 3a–f are rather weak. The wide scatter is due to the wide diversity of local topographic conditions and is unsurprising as it has been shown in various other studies how glaciers with similar climates can have very different dimensions and characteristics (e.g. Kuhn and others, 1985; Andreassen and others, 2008; Abermann and others, 2009).

The negative glacier changes between the two glacier inventories can be attributed to almost continuous positive temperature anomalies since 1981 throughout the study area, which is consistent with climate change interpretations made in globally directed studies (e.g. Solomon and others, 2007). Successive positive temperature anomalies amplify their own effect on a glacier’s mass balance due to feedback mechanisms (e.g. albedo, heat conduction from surrounding terrain) as described in recent publications (e.g. Oerlemans and others, 2009; Fischer, 2010).

Individual years of positive mass and area changes in the late 1970s and early 1980s have been reported previously (Patzelt, 1985; Abermann and others, 2009). Figure 5 allows the attribution of these positive mass and area changes to changes in atmospheric conditions qualitatively: there was a sequence of negative temperature anomalies throughout the study area between 1974 and 1981 combined with some positive precipitation anomalies (Fig. 5).

Anomalies in winter precipitation have a less distinct temporal evolution than temperature anomalies. All regions show negative cumulative anomalies in total. While the period 1969–98 was marked by negative area and mass changes in Austrian glaciers, a sequence of positive anomalies of winter precipitation was observed (e.g. 1974 –83), especially in the western part of the country (regions A and B). The significantly more negative precipitation anomalies in regions C and D after 1983 add an argument for less negative glacier changes in A and E.

A reason why glacier changes in region B are more negative than, for example, in regions A and E, despite very similar precipitation and temperature anomalies, could be found by investigating the typical morphology of the glaciers in this region. Glaciers in region B consist of a relatively high fraction of low-lying (and comparably thick) valley glaciers that tend to react more strongly and on a longer timescale to climatically induced change. The extremely low glacier flow velocity values measured in recent years, for example on the Kesselwandferner (Abermann and others, 2007) and the Hintereisferner (Span and others, 1997), suggest an additional dynamic reason for the stronger recession: ice supply is reduced and the dynamically supported downwasting of these low-lying thick tongues follows as a direct consequence. Therefore, regionally varying temperature and precipitation anomalies alone cannot explain the regionally varying glacier change as shown in Figures 4 and 5.

Absolute values of mean precipitation should be interpreted with care because of the lack of altitudinal information in the dataset. However, in this study we base the line of argument on spatial differences of precipitation or temporal deviations from the mean and do not use absolute values for interpretation. It has been shown that anomalies of high and low elevations evolve similarly (Auer and others, 2005), which justifies the qualitative use of this dataset.

Conclusions

We have investigated the relationship between climatic parameters and glacier distribution in the Austrian Alps. Spatial differences in 1969–98 glacier changes can be attributed mainly to regional differences in local topography.

We found a relationship between glacier median elevation, glacier minimum elevation and mean winter precipitation. Spatial temperature gradients alone cannot explain the regionally very different glacier extents, but support the general pattern caused by spatial precipitation differences and general topographic conditions.

Since only basic glaciological data are required for this study, similar analyses are planned in other climatic regions. The inclusion of German, Swiss, Italian and Slovenian glaciers would allow an analysis of Alps-wide glacier changes and spatial gradients of their climatic setting. Meteorological data are also restricted to basic parameters: mean summer temperature including spatially varying lapse rates and mean winter precipitation which makes the analysis easy to apply over large areas.

Responding to the large glacier changes of the past decade, Abermann and others (2009) initiated a third lidar-based glacier inventory, which will soon be available as a database with which to continue investigations of regional climate change and its impact on glacier changes in the present and recent past.