Creep experiments and numerical simulations of very light artificial snowpacks

Abstract

This paper reports on the measurement of the viscosity coefficient of very light artificial snow with H. density of < 100 kg m^−3. The temperature dependency on the viscosity coefficients of the snow was also obtained, and these results were applied to the problem of snow creep. General comparison between experimental and computed results shows good agreement, but differences between the two creep flows along the slope indicate that low-density snow near the freezing point should be considered as an orthotopic material.

Introduction

The mechanical properties of very light snow affect the avalanche release in the first stage immediately after a snowfall. There are only a few data on the viscosity coefficient of a linearly viscous fluid model for low-density snow of < 100 kg m⁻³, and still fewer on its temperature dependency (Nakamura, 1988; Endo and others, 1990; Kominami and others, 1998). On the other hand, the problems of snow creep have been investigated by many researchers (e.g. Bader and others, 1954; Lang and Sommerfeld, 1977; Salm, 1977; McGlung and Larsen, 1989; Olagne and McGlung, 1990). However, creep tests on low-density snow have not been attempted for a long time.

Measurements

Cryospheric Environment Simulator (GES)

To obtain the viscosity coefficient of very light snow, artificial snow made in the Cryospheric Environment Simulator (CES) was used. The CES was established at the Shinjo Branch of Snow and Ice Studies, National Research Institute for Earth Science and Disaster Prevention, in 1997 (Higashiura and others, 1997). This facility includes an artificial snowfall machine which grows a large number of crystals from the vapor phase. A snow particle has one or two branches of a dendritic crystal, i.e. the snow particle is a frost crystal (Fig. 1). The maximum intensity of snowfall is 1 mm h⁻¹ we. The density of the snow immediately after snowfall is approximately 20 kg m⁻³.

Fig. 1. Artificial snow particles.

Viscosity coefficients of low-density snow

Densities of newly fallen dry snow are usually in the range 20–100 kg m⁻³ (Nakamura, 1986). Below 0°C and under calm conditions very light snow with a density of <50kg m⁻³ is sometimes observed. Endo and others (1990) reported that the relationship between the viscosity coefficient ηPa s) and the snow density p (kg m⁻³) of < 180 kg m⁻³ is expressible as

(1)

where C (Pas (kg m⁻³)-n) is a constant and n is a nearly constant power coefficient with a value of approximately 4.00. Endo and others measured the viscosity coefficient of compression for dry snow.

For processes of long duration snow is considered as a linearly viscous material, so that the compressive viscosity coefficient of snow is defined by the following equation (Kojima, 1955):

(2)

where W is the load on a snow layer (Pa) including half of its weight, and v is strain rate (s⁻¹).

To obtain the viscosity coefficient of low-density snow, a strain meter was installed over each snowpack as shown in Figure 2. The cubic specimens of the snowpacks were 0.9 × 0.9 m², and the heights were initially 0.13–0.36 m. The applied load on each snowpack was kept constant during the measurement. Using Equation (2), the compressive viscosity coefficient was calculated from the load and strain rate of the snow. Figure 3 shows the viscosity coefficient vs the snow density as measured in this study. The snow densities used here were 20–100 kg m⁻³, and the snow temperatures were controlled to be –5°, –11°, –14° and –19.5°C, respectively. The solid line in Figure 3, reported by Endo and others (1990), for dry snow in the temperature range –5° to 0°C, matches the present results for a snow temperature of –5°C. The viscosity coefficient for –11 ° and –19.5°C is greater than that for –5°C. From these results, using the least-squares method, the temperature dependency of the constant C in Equation (1) is estimated as follows (Fig. 4):

(3)

where T_s is the snow temperature in°C, and C is obtained in Pas (kg m⁻³)-n. Equations (1) and (3) will be used for numerical simulations later on.

Fig. 2. Strain meters installed over the snow_Packs.

Fig. 3. Viscosity coefficient vs snow density.

Fig. 4. Temperature dependency on the viscosity coefficient.

Creep experiments

Creep experiments using very light artificial snow on a slope were carried out under different temperatures in the CES. The maximum snowpacks were 5 m long, 3 m wide and 0.5 m high. The initial densities of the snow were in the range 30–57 kg m⁻³. In the experiment a snowpack was initially formed on a table (5 m × 3 m), maintained at this position for several hours, then the table was inclined at a fixed angle. The snowpack was fixed to a carpet frozen onto the table, thus preventing the snow from gliding down the slope. To observe the deformation of the snow, cross marks were sprayed on the side at 0.1m intervals using blue ink with water, and chopsticks were horizontally inserted at the center of the cross marks.

Figures 5a and 6a show side views of the center of the snowpack on the table every 24 h for a period of 3 days at –19.5°C and –11°C. In both cases the slope angles were maintained at 30°. The deformation of the snowpack at –11°C is faster than that at –19.5°C. In the following section these results are compared with numerical simulations.

Fig. 5. Comparison of the deformation between experimental (a) and computed (b) results at a snow temperature of-19.5° C.

Fig. 6. Comparison of the deformation between experimental (a) and computed (b) results at a snow temperature of –11°C

Numerical Simulations

Constitutive equation for snow deformation

The constitutive equation between the stress and strain rate for isotropic materials was established by Lang and Nakamura (1984) as a viscous body. For plane strain it is as follows:

(4)

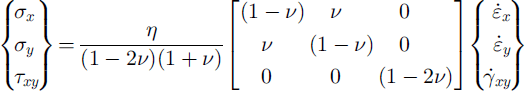
where a and τ are the tensile and shear stresses respectively, _η and v are the viscosity coefficient and Poisson’s ratio, and and are the tensile and shear strain rates at .

The computer program used to model the creep problem is a finite-element code which can be used to analyze linear orthotropic planar elasticity problems (Lang and others, 1984). This program was applied to evaluate snow-settlement problems by Lang and Nakamura (1984) and Nakamura (1988).

Initial conditions

In the numerical simulations the layout of the element array was considered as shown in Figure 7. The modeled snow-pack consists of four or five layers. The left (lower) and right (upper) sides of the snowpack with a width of 1 m were disregarded because the snowpack had sufficient length (3 m) compared with its height (0.5 and 0.36 m, respectively). The bottom nodal points are assumed to be fixed on the table, as was the case for the experimental conditions. The initial snow densities used in this model are measured for each layer at the initial stage of the experiments. Poisson’s ratio is considered to be 0.27 of an average of compression and tension (Shinojima, 1967).

Fig. 7. Element layout and initial conditions for numerical simulation at a snow temperature of-19.5° C.

Time incrementation

Time incrementation is conducted using the following procedure.

1. (1) Calculate the viscosity coefficient for each element from the snow density and temperature using Equations (1) and (3).

2. (2) Calculate the deformation of each nodal point lhour later with the finite-element model using Equation (4).

3. (3) Calculate the snow density for each element from the deformation based on the conservation law of mass.

4. (4) Repeat steps (1–3) by stepping forward in time. In this procedure the snow temperature is considered to be constant as measured at the initial experimental conditions. The driving force is gravity.

Computed results

The results of the computer simulation are shown together with the experimental results in Figures 5b and 6b for temperatures –19.5° and –11 °C, respectively. Satisfactory agreement was obtained in general, but slight differences can be observed in Figure 6 for temperatures of –11°C.

Discussion and Conclusions

A formula was developed for the density dependence of the compressive viscosity of a viscous model for very light artificial snow. Laboratory creep experiments were conducted on a slab of this snow on an inclined plane, and the deformation of an initially rectangular grid was observed for three consecutive days. Assuming plain strain and a linear viscous law (with constant Poisson’s ratio), this deformation was computationally reproduced (by simultaneously imposing the basal no-slip condition).

Good agreement of the deformations between the experimental and computed results suggests that the viscosity coefficients for low-density snow measured here can be generally applied to snow creep. However, the low-density snow at high temperatures should be considered to be an orthotropic material, because the snowpack at a temperature of –11°C is slippery as compared with the model snow which is considered to be an isotropic material. Yamada and others (1974) reported that the physical properties of snow are strongly sensitive to its texture, particularly in new snow. Furthermore, snow under stress changes its microstructure even at high density (Edens and Brown, 1991). Figure 8 shows a thin vertical section of a snow specimen on the slope 9 days after the start of the experiments in snow temperatures of –19.5°C and with a slope angle of 30°, in which the bottom is parallel to the slope. In this figure the microstructure of the snow is quite different between the directions perpendicular and parallel to the slope, because most of the ice columns tend to run parallel to the slope. Thus low-density snow has different properties in different directions depending on the acting stress. The constitutive equation of orthotropic behaviour is needed to describe snow creep near the freezing point.

Fig. 8. Thin vertical section of a snow specimen on a table.