Introduction
Significant progress in knowledge of the rheological properties of ice has been made possible by the study of the ice structure from deep ice cores. Variations in grain-size and the development of lattice-preferred orientations (fabrics) in response to changing temperature, stresses and impurities are directly related to different physical processes. At high stresses, the non-linear constitutive law with a stress exponent equal to three is observed (Reference PatersonPaterson, 1983; Reference Lipenkov, Salamatin and DuvalLipenkov and others, 1997). At low stresses, a stress exponent lower than 2 seems to be verified mainly from borehole-deformation measurements (Reference Mellor and TestaMellor and Testa, 1969; Reference Doake and WolffDoake and Wolff, 1985; Reference Dahl-Jensen and GundestrupDahl-Jensen and Gundestrup, 1987) and bubbly-ice densification (Reference Lipenkov, Salamatin and DuvalLipenkov and others, 1997).
With regard to physical processes involved in the deformation of polar ice, conflicting results are still found in spite of new data from the study of deep ice cores. From Reference Goldsby and KohlstedtGoldsby and Kohlstedt (1998) and Reference Tarasov, Peltier, Goldsby and KohlstedtTarasov and others (1998), grain-boundary sliding would often be the dominant creep mechanism in polar ice sheets. A value of the stress exponent close to 1.8, at stresses lower than 0.1 MPa, would indicate that superplastic flow is occurring extensively in ice sheets. These conclusions are obviously in conflict with the development of fabrics, interpreted by numerous authors as the rotation of the lattice by intracrystalline slip (Reference Azuma and HigashiAzuma and Higashi, 1985; Reference AlleyAlley, 1992; Reference AzumaAzuma, 1994; Reference Castelnau, Duval, Lebensohn and CanovaGastelnau and others, 1996b; Reference Godert and HutterGodert and Hutter, 1998; Reference Gagliardini and MeyssonnierGagliardini and Meyssonnier, 1999).
A more complex response prevails for so-called tertiary creep. Initially polycrystalline isotropic ice deformed in the laboratory exhibits a primary decelerating creep associated globally with the redistribution of stress within the polycrystal, as the softer creep-slip systems relax. Beyond the minimum creep-rate stage, the creep rate accelerates into tertiary creep and a steady state is observed at a strain of about 10% (Reference Jacka and MaccagnanJacka and Maccagnan, 1984; Reference Budd and JackaBudd and Jacka, 1989). This steady state is associated with the formation of textures with interlocking grains and fabrics with crystals well-oriented for basal slip (Reference DuvalDuval, 1981). This tertiary creep is clearly involved in temperate glaciers and in the deepest ice layers of ice sheets (Reference Gow and WilliamsonGow and Williamson, 1976; Reference GowGow and others, 1997; Reference Thorsteinsson, Kipfstuhl and MillerThorsteinsson and others, 1997).
It seems difficult to assert that this tertiary creep is occurring in the major part of ice sheets. From Reference De la Chapelle, Castelnau, Lipenkov and DuvalDe la Chapelle and others (1998), tertiary creep is associated with migration recrystallization which involves a high grain-boundary-migration-rate regime. Stable fabrics are formed for a strain lower than 10% Reference Jacka and MaccagnanJacka and Maccagnan, 1984). This behavior does not correspond to the slow development of fabrics observed in ice sheets from the surface and induced by the rotation of the lattice by slip. The variation of the ice texture with depth results from normal grain growth near the surface and from rotation recrystallization (Reference Pimienta and DuvalPimienta and Duval, 1987; Reference AlleyAlley, 1992). Rotation recrystallization is associated with the nucleation of grains by the progressive misorientation of sub-boundaries and with a regime where grain boundaries migrate in the same low-velocity regime as that associated with normal grain growth (Reference De la Chapelle, Castelnau, Lipenkov and DuvalDe la Chapelle and others, 1998). This recrystallization regime appears to slow down fabric development (Reference Castelnau, Thorsteinsson, Kipfstuhl, Duval and CanovaGastelnau and others, 1996a). With these assumptions, a steady state cannot be invoked and, depending on the imposed velocity gradients, strain rates lower than those corresponding to secondary creep observed in the laboratory can be found.
In order to improve the interpretation of fabrics in ice sheets and to determine the relation between fabrics and the instantaneous mechanical behavior, polycrvstal models based on a micro-macro approach were developed recently (Reference AzumaAzuma, 1994, Reference Azuma1995; Reference Castelnau, Duval, Lebensohn and CanovaCastelnau and others, 1996b, Reference Castelnau, Canova, Lebensohn and Duval1997; Reference Godert and HutterGodert and Hutter, 1998; Reference Gagliardini and MeyssonnierGagliardini and Meyssonnier, 1999). Predictions of fabric development by these models are generally in agreement with measurements. Concerning the charactenzation of the mechanical behavior of anisotropic ices, significant differences between models, however, are found.
This work is focused on the analysis of deformation and recrystallization processes which occur in ice sheets. Special emphasis is placed on the occurrence of both rotation and migration recrystallization. An estimate of the energy stored within deep ice of the Vostok core is made from X-ray diffraction imaging carried out at the European Synchrotron Radiation Facility (ESRF, Grenoble).
Deformation Modes of Polar Ice
At high deviatoric stresses (>0.2MPa), the stress exponent for the polycrystal is close to 3. During primary creep, strain rate decreases by more than three orders of magnitude (Reference JackaJacka, 1984). On first loading, the stress state within polycrystalline ice is almost uniform. However, owing to the very large plastic anisotropy of ice crystals, the resolved stress on the basal plane on each grain relaxes and the load is transferred to the harder slip systems (Reference Duval, Ashby and AndermanDuval and others, 1983). As a result, an increasingly nonuniform state of internal stress develops. The anisotropic viscoplastic self-consistent (VPSC) model used by Reference Castelnau, Canova, Lebensohn and DuvalCastelnau and others (1997), for predicting the mechanical behavior of polycrystalline ice and fabric development, reproduces the macroscopic behavior of isotropic and anisotropic ice very well by assuming that ice crystals deform by dislocation glide on basal, prismatic and pyramidal planes. The resistance of these slip systems was determined by an inverse approach, based on a comparison between model results and results of several mechanical tests. It was shown that the VPSC estimate of the rheology of in-situ grains matches that obtained experimentally on isolated crystals. The static model (uniform stress within the polycrystal) can reproduce the macroscopic behavior of anisotropic polycrystalline ice, but only by imposing a resistance to the basal slip systems much higher than that deduced from the behavior of isolated monocrystals (Reference Castelnau, Canova, Lebensohn and DuvalCastelnau and others, 1997).
At low deviatoric stresses ( <0.2 MPa), the value of the stress exponent corresponding to secondary creep for which the creep rate reaches a minimum value is < 2 (Reference Mellor and TestaMellor and Testa, 1969; Reference Duval and CastelnauDuval and Castelnau, 1995). This laboratory result is supported by field measurements (Reference Doake and WolffDoake and Wolff, 1985; Reference Lliboutry and DuvalLliboutry and Duval, 1985; Reference Dahl-Jensen and GundestrupDahl-Jensen and Gundestrup, 1987). A polynomial flow law with n = 1 at low stresses was obtained by Reference Lipenkov, Salamatin and DuvalLipenkov and others (1997) from the densification of bubbly ice. This law has already been suggested by Reference LliboutryLliboutry (1969) and Reference HutterHutter (1983).
Creep experiments were recently carried out on finegrained ice (grain-size ranging from 8–89 pm) samples by Reference Goldsby and KohlstedtGoldsby and Kohlstedt (1997) to obtain accurate data on the flow law at low stresses. A regime with n = 1.8 was found at low stresses with a grain-size dependence ![]() giving p = 1.4. According to these authors, grain-boundary sliding would be the dominant creep mechanism in the n = 1.8 regime. Extrapolation of this flow law to grain-sizes of 1mm or larger, i.e. for conditions prevailing in ice sheets, would indicate that grain-boundary sliding would often be a dominant mechanism of deformation in large ice sheets (Reference Goldsby and KohlstedtGoldsby and Kohlstedt, 1998). This conclusion is not in accordance with the development of fabrics induced by the rotation of the lattice by dislocation slip (Reference Azuma and HigashiAzuma and Higashi, 1985; Reference Castelnau, Duval, Lebensohn and CanovaCastelnau and others, 1996b). Figure 1 shows both the observed fabric at 622 m depth for the Vostok ice core (Fig. 1a) and that simulated by the VPSC model used by Reference Castelnau, Duval, Lebensohn and CanovaCastelnau and others (1996b) for an equivalent strain of 0.25 corresponding to the estimated equivalent strain at this depth (Fig. 1b). Figure 1 also shows the fabric obtained by the VPSC model by assuming that grain-boundary sliding represents 80% of the total strain (Fig. 1c). It is clear that the assumption of Goldsby and Kohlstedt does not hold for polar ice. Intracrystalline dislocation glide should be the predominant deformation mode of polar ice at high and low stresses.
giving p = 1.4. According to these authors, grain-boundary sliding would be the dominant creep mechanism in the n = 1.8 regime. Extrapolation of this flow law to grain-sizes of 1mm or larger, i.e. for conditions prevailing in ice sheets, would indicate that grain-boundary sliding would often be a dominant mechanism of deformation in large ice sheets (Reference Goldsby and KohlstedtGoldsby and Kohlstedt, 1998). This conclusion is not in accordance with the development of fabrics induced by the rotation of the lattice by dislocation slip (Reference Azuma and HigashiAzuma and Higashi, 1985; Reference Castelnau, Duval, Lebensohn and CanovaCastelnau and others, 1996b). Figure 1 shows both the observed fabric at 622 m depth for the Vostok ice core (Fig. 1a) and that simulated by the VPSC model used by Reference Castelnau, Duval, Lebensohn and CanovaCastelnau and others (1996b) for an equivalent strain of 0.25 corresponding to the estimated equivalent strain at this depth (Fig. 1b). Figure 1 also shows the fabric obtained by the VPSC model by assuming that grain-boundary sliding represents 80% of the total strain (Fig. 1c). It is clear that the assumption of Goldsby and Kohlstedt does not hold for polar ice. Intracrystalline dislocation glide should be the predominant deformation mode of polar ice at high and low stresses.
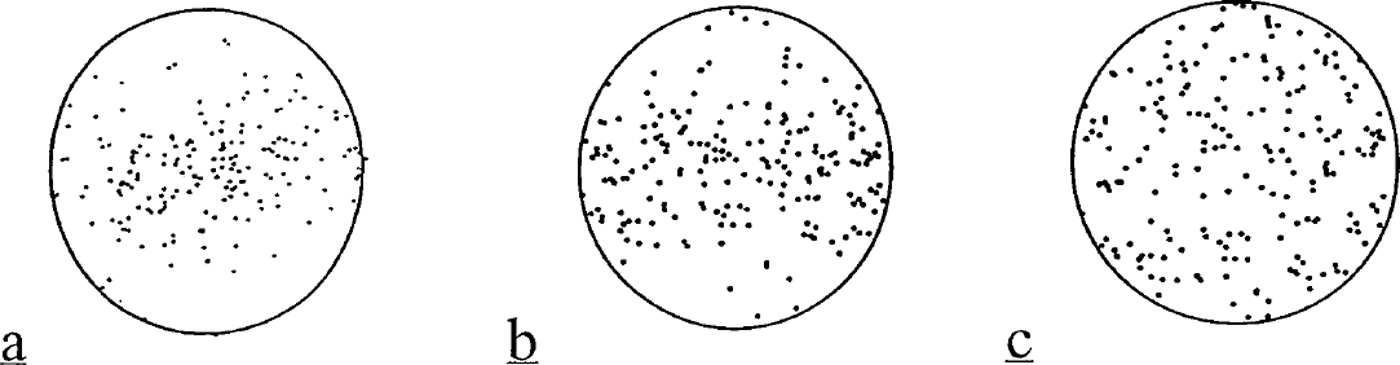
Fig. 1. (a) The fabric pattern of the Vostok ice core for 622 m depth compared with fabrics calculated using the VPSC model in uniaxial extension with (b) an equivalent strain of 0.25 and ( c) an equivalent strain of 0.05 (20% of the total strain; grain-boundary sliding being assumed to represent 80% of the total strain).
We suggest that deformation of polar ice at low stresses, when migration recrystallization does not occur, is produced by intracrystalline slip accommodated by grain-boundary migration (gbm) linked to grain growth or rotation recrystallization (Reference Duval and CastelnauDuval and Castelnau, 1995). The generation of dislocations during deformation is given by :
where ![]() is the strain rate; the dislocation-free path, d, is assumed to correspond to the grain-size when grain growth is occurring and to the subgrain-size when rotation recrystallization is occurring.
is the strain rate; the dislocation-free path, d, is assumed to correspond to the grain-size when grain growth is occurring and to the subgrain-size when rotation recrystallization is occurring.
From Reference De la Chapelle, Castelnau, Lipenkov and DuvalDe la Chapelle and others (1998), the main process for the reduction of the dislocation density is gbm associated with grain growth or rotation recrystallization. If we neglect other recovery processes (dislocation climb, etc.), the reduction in the dislocation density by gbm is given by:
where K is the gbm rate and α is a coefficient exceeding 1, which makes it possible to take into account a higher dislocation density near grain boundaries.
The reduction of the dislocation density by the formation of boundaries associated with rotation recrystallization is not taken into account. With these assumptions, the evolution of the dislocation density within grains during deformation can be obtained. Calculation of the dislocation density along the Vostok core indicates that the driving force for the initiation of migration recrystallization is not reached (Reference De la Chapelle, Castelnau, Lipenkov and DuvalDe la Chapelle and others, 1998).
Information on the distortion of the lattice on Vostok samples was obtained by X-ray diffraction imaging at the ESRF. Figure 2a shows a topograph of a 5 mm thick ice crystal at 3286 m depth with reflection on the basal plane (0002 reflection). Figure 2b shows a section topograph of the same crystal (0002 reflection). The horizontal beam width was restricted to 300 μm. The diffracting image corresponds to a part of a thin tube with the symmetry axis along the c axis. This three-dimensional structure is clearly displayed on the section topograph. The rocking curves do not exhibit the presence of sub-boundaries, but indicate a continuous change in lattice orientation, as produced by the three-dimensional distribution of dislocations. This structure should be produced by the ice crystal bending through isolated basal dislocations. The dislocation density deduced from these measurements, of the order of 1010 m−2, is in accordance with that deduced from Equations (1) and (2) (Reference De la Chapelle, Castelnau, Lipenkov and DuvalDe la Chapelle and others, 1998). Migration recrystallization cannot be involved in this sample even if the in-situ temperature is above –10°C

Fig. 2. (a) X-ray diffraction topographs of a 5 mm thick ice crystal from the Vostok ice core (3286 m depth; 0002 reflection). (b) X-ray diffraction section topograph of the same sample (0002 reflection).
Dynamic Recrystallization and Tertiary Creep
In order to clarify the relationship between dynamic recrystallization, creep behavior and the development of fabrics, recent results obtained by Reference Jacka, Li and HondohJacka and Li (in press) appear very useful. Figure 3 shows a creep curve obtained in uniaxial compression at –21°C. The fabric pattern observed after a strain of about 8% is very weak. On the other hand, the minimum creep rate attained at about 1% strain is maintained up to the end of the experiment. This new result indicates that migration recrystallization was not occurring and that the development of the fabric was mainly induced by deformation. We assume that rotation recrystallization associated with the slow gbm rate was occurring during this test. Figure 4 shows the usual creep curve obtained at –3°C also in uniaxial compression (fromReference Jacka and MaccagnanJacka and Maccagnan, 1984). A circle girdle fabric around the compression axis is obtained. The observed structure with interlocking grains indicates that migration recrystallization was the main recrystallization process. The ratio between the tertiary strain rate and the minimum creep rate is about 3 in uniaxial compression and tension and about 10 in simple shear (Reference DuvalDuval, 1981; Reference Budd and JackaBudd and Jacka, 1989). The high tertiary strain rate is due to both the formation of anisotropic ice and softening processes associated with gbm.
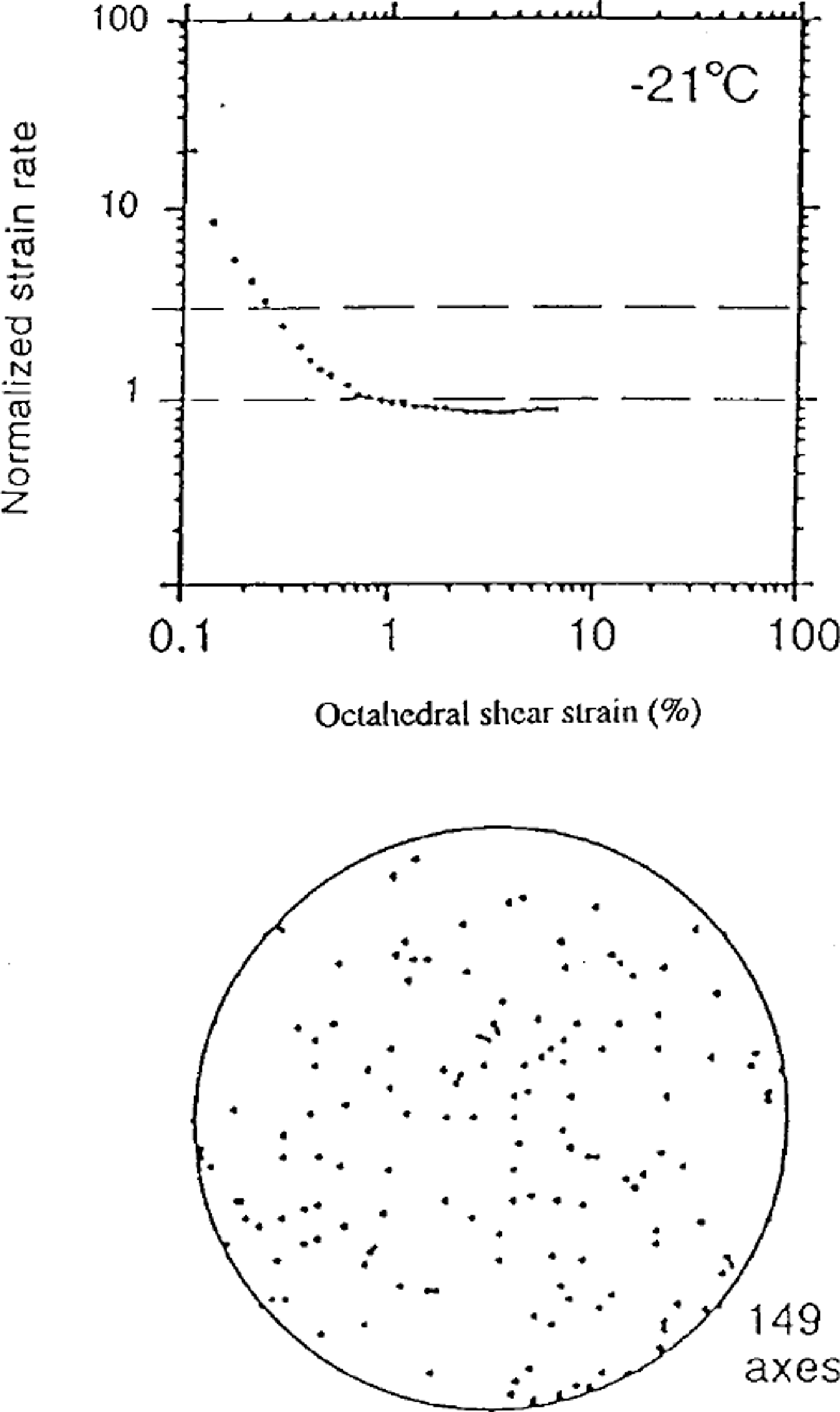
Fig. 3. Creep curve and fabric data for an intially isotropic ice sample deformed in uniaxial compresion at 0.2 MPa. (from Reference Jacka, Li and HondohJacka and Li, in press).
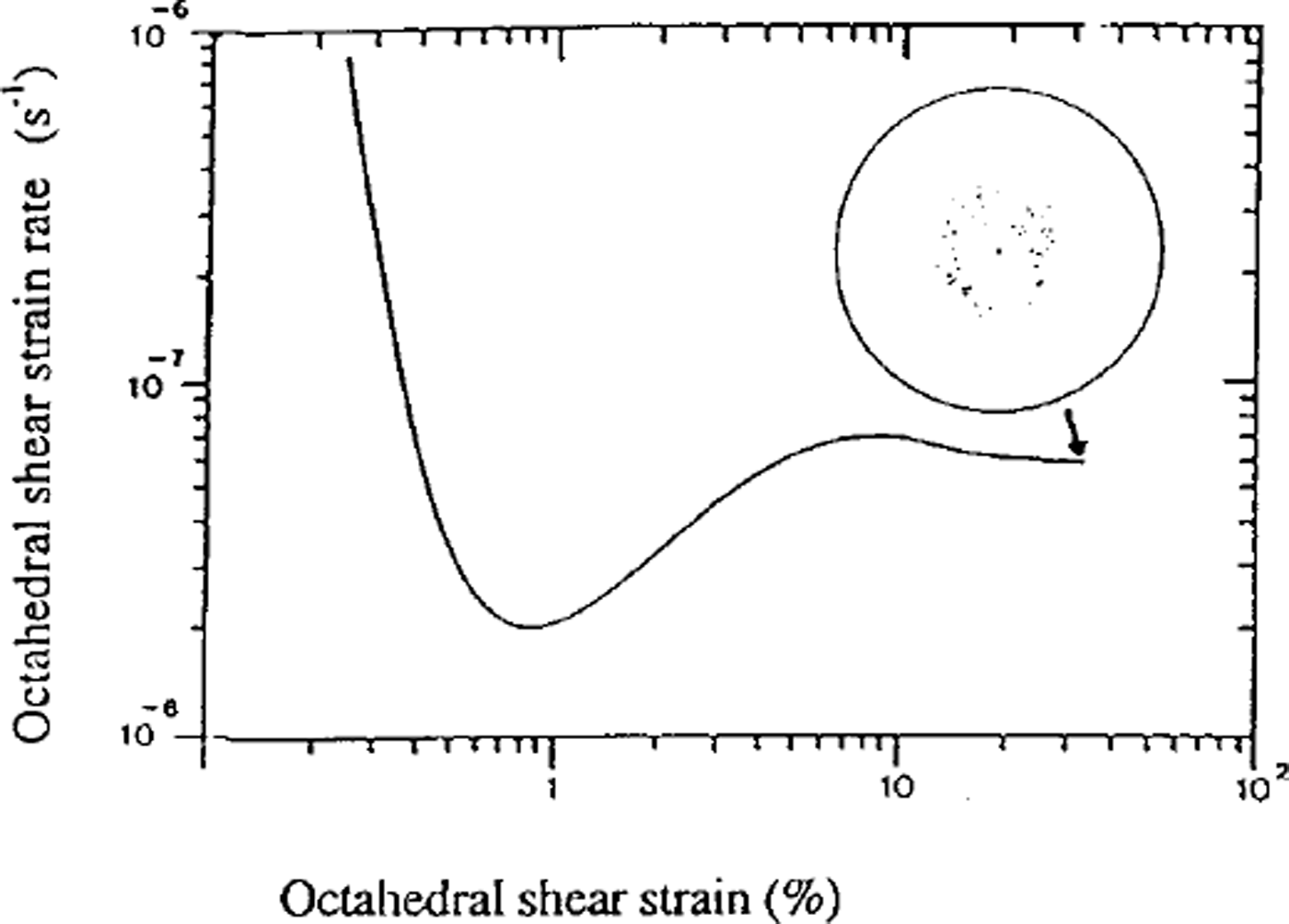
Fig. 4. Creep curve and crystal fabric at a strain of 0.32for an intially isotropic ice sample deformed at 0.2 MPa. and a temperature of–3.0°C (from Reference Jacka and MaccagnanJacka and Maccagnan, 1984).
The marked difference between fabric development and recrystallization mechanisms is clearly displayed in the Byrd ice core (Reference Gow and WilliamsonGow and Williamson, 1976). Figure 5 illustrates this transition between rotation and migration recrystallization in the Greenland Icecore Project (GRIP) ice core. At 2806 m depth, a tight clustering of the c axes around the vertical is found with a fine-grained structure. At 2862 m depth, an open fabric is observed and the ice consists of large, interlocking grains. The fine-grained structure is associated with glacial ice whereas the coarse-grained ice is associated with interglacial ice. The gbm is probably dependent on the impurity content and the fast gbm regime observed in interglacial ice indicates that impurities do not alter gbm (Reference Thorsteinsson, Kipfstuhl and MillerThorsteinsson and others, 1997).

Fig. 5. Photographs of thin sections in polarized light and crystal fabrics in the GRIP ice core at 2806m (top) and 2862 m (bottom) (from Reference Thorsteinsson, Kipfstuhl and MillerThorsteinsson and others, 1997).
With regard to the creep behavior associated with rotation recrystallization, the creep curve shown in Figure 3 is one example. The "steady state" probably corresponds to a true equilibrium between strain hardening and softening processes. The insignificant effect of the fabric development is related to the slow fabric development by slip. However, a slow decrease of the strain rate is expected at large strains as soon as anisotropic ice forms.
The creep behavior when only the "normal" grain growth is occurring is interesting, i.e. in the upper layers of ice sheets (Reference Alley and WoodsAlley and Woods, 1996; Reference De la Chapelle, Castelnau, Lipenkov and DuvalDe la Chapelle and others, 1998). Grain-boundary migration is induced by the decrease of the free energy of grain boundaries. It therefore occurs at a rate which is independent of strain rate. However, as explained above, strain rate is dependent on grain growth since gbm accommodates dislocation glide. The consequence of this is that the creep behavior associated with grain growth is dependent on the velocity of gbm. At small strain rates, the transient creep should be partly suppressed and the ice viscosity could be much lower than that extrapolated from higher strain rates. A stress exponent lower than 3 is therefore expected (Reference Pimienta and DuvalPimienta and Duval, 1987; Reference AlleyAlley, 1992). Obviously, this behavior cannot be observed in the laboratory.
Conclusion
The study of the structure of deep ice cores from polar ice sheets has provided important information on the occurrence of recrystallization processes and the formation of fabrics along the cores.
Due to the difficulty of making laboratory experiments under real in-situ conditions, conflicting results on the deformation modes of polar ice are found. Several data from ice cores support the assumptions of the preponderance of dislocation slip for the deformation of polar ice. Intracrystalline slip would be accommodated by grain-boundary migration associated with normal grain growth or rotation recrystallization. The well-known tertiary creep, associated with migration recrystallization, can be invoked only near the bottom of ice sheets. However, it is not observed in the Vostok core because the driving force is not sufficiently large to initiate this recrystallization process.
At low stresses, the value of the stress exponent associated with the normal grain growth should be φ2. From tests performed at low stresses in the laboratory, the stress exponent also appears to take a value ≤ 2 when rotation recrystallization is occurring.
Acknowledgements
This work was supported by the CNRS (Departement des Sciences pour l’lngénieur) and the Commission of European Communities (CEC) Environment and Climate Programme (EU Project: Fabric development and rheology of polar anisotropic ice for ice sheet flow modelling (1996–1999)). We are very grateful to T. H. Jacka and Li Jun for fruitful discussions and for allowing us to use their results. The authors are very grateful to J. Baruchel and J. Hartwig, from the European Synchrotron Radiation Facility, for advice and fruitful discussions on X-ray diffraction topography experiments performed there.






