DEM quality assessment for quantification of glacier surface change

Abstract

Photogrammetric digital elevation models (DEMs) are often used to derive and monitor surfaces in inaccessible areas. They have been used to monitor the spatial and temporal change of glacier surfaces in order to assess glacier response to climate change. However, deriving photogrammetric DEMs of steep mountainous topography where the surface is often obscured by regions of deep shadow and snow is particularly difficult. Assessing the quality of the derived surface can also be problematic, as high-accuracy ground-control points may be limited and poorly distributed throughout the modelled area. We present a method of assessing the quality of a derived surface through a detailed sensitivity analysis of the DEM collection parameters through a multiple input failure warning model (MIFWM). The variance of a DEM cell elevation is taken as an indicator of surface reliability allowing potentially unreliable areas to be excluded from further analysis. This analysis allows the user to place greater confidence in the remaining DEM. An example of this method is presented for a small mountain glacier in Svalbard, and the MIFWM is shown to label as unreliable more DEM cells over the entire DEM area, but fewer over the glacier surface, than other methods of data quality assessment. The MIFWM is shown to be an effective and easily used method for assessing DEM surface quality.

1. Introduction

Glaciologists have become increasingly dependent on the use of digital elevation models (DEMs) to analyze topographic landforms and as an input for further modelling. DEMs are particularly useful for monitoring and mapping both spatial and temporal change, as large areas can be modelled with only minimal field-based input. For this reason, DEMs provide a useful method of monitoring glacier surface change. Observing glacier mass balance is seen as a critical indicator of climate change and, importantly, helps quantify the volume of water being released into the oceans, raising global sea levels. However, only a handful of glaciers have been the subject of long-term mass-balance investigations (Meier, 1984; Dyurgerov and Meier, 1997; Dyurgerov, 2000). Projected rates of global sea-level rise in response to climate change can be criticized for using such a small sample, especially since it is not evenly distributed throughout the glaciated regions of the Earth (Braithwaite, 2002).

Glacier surface change derived from remote sensing does not produce detailed interannual records like the traditional mass-balance technique, but it does offer a way to increase significantly the number of glaciers for which we have knowledge of their surface change through time (Etzelmüller and Sollid, 1997; Fox and Nuttall, 1997; Fox and Gooch, 2001). Photogrammetrically derived DEMs are particularly useful, with image data spanning >60 years available in some regions. This historical and relatively untapped archive allows glaciologists to assess the long-term surface change of glaciers that have never been the subject of mass-balance studies. If several surveys have been carried out over a glacier, rates of change can also be investigated.

Software that allows semi-automated DEM collection has become relatively accessible and has greatly increased the use of the photogrammetry technique. However, many studies have been criticized for failing to adequately estimate surface reliability and accuracy. This criticism has led to some calculations of sea-level rise excluding results derived using digital photogrammetry (Dowdeswell and others, 1997; Dyurgerov and Meier, 1997; Braithwaite, 2002). Ensuring that the photogrammetric DEM surface is reliable is therefore crucial if this method is to be used with confidence.

In this paper, a number of methods that assess surface reliability are investigated. Each technique is tested for the area around a small valley glacier, austre Brøggerbreen, Svalbard, which is surrounded by steep mountains and has an undulating forefield (Fig. 1). The performance of these reliability indication methods is compared in particular for the identification of unreliable regions across the glacier surface. The most basic method is the use of the statistical confidence of matching produced during the stereo-matching procedure. The second method is a failure warning model (FWM) developed by Gooch and Chandler (2001), which uses the sensitivity of a cell’s elevation to changes in the DEM collection parameters. The final method develops this method further by calculating cell variance for a number of input DEMs collected with different parameters. We show that the latter technique is an improvement on the other two and can be used easily and efficiently to assess DEM reliability. Finally we demonstrate the method using photographs from 1970 and 1990 to create a difference DEM for austre Brøggerbreen.

Fig. 1. Geo-rectified aerial image showing part of the Brøggerhalvøya peninsula with austre Brøggerbreen outlined. Image reproduced courtesy of the Norwegian Polar Institute. (Image 6456 from the 1990 1 : 50 000 series.)

2. Data

The aerial images used in this study are from the 1990 1 : 50 000 series commissioned by the Norwegian Polar Institute (NP). The images were supplied as diapositives which were scanned at a density of 17 μm, resulting in a pixel size of about 0.7 m. Ground-control points (GCPs) were collected around the glacier during a field campaign in spring 2002 using the differential global positioning system (GPS). Positional accuracies of around ±0.05m were achieved during this survey, but unfortunately, due to the steepness of the mountains, most GCPs were located around the front of the glaciers. To overcome this problem, an older set of GCPs that fixed the position of many nearby mountain tops was supplied by NP. These GCPs were surveyed optically and should be sufficiently accurate, although their accuracy was degraded slightly during their conversion from European Datum 1950 (ED50) to World Geodetic System 1984 (WGS84). This degradation is not expected to affect the results to any significant degree. All photogrammetry was undertaken using ERDAS Imagine OrthoBASE software.

3. Assessing Surface Reliability

Before discussing indicators of surface reliability, it is important to define some terms (more detailed definitions may be found in Cooper and Cross, 1991). Accuracy is defined as the difference between the modelled DEM surface and the actual ground surface. Accuracy can be quantified by comparing the modelled surface to another dataset of higher accuracy, usually surveyed ground-truth data. Reliability is the ability to repeatedly model a surface and return the same value each time. The smaller the difference between returned values, the more reliable the surface may be considered to be.

The advantage of investigating surface reliability is that it is possible to quantify reliability over the entire DEM surface. The accuracy can only be defined where there is ground control, and while the DEM may easily contain over 500 000 cells the number of GCPs is unlikely to exceed 100. A surface may, however, be reliable but inaccurate, and reliability tests are not a replacement for rigorous accuracy assessments. Reliability assessments are, though, the only method to investigate the DEM surface where there is no ground control.

3.1. Matching statistic

The degree of confidence that a match between the two image pairs is correct can be calculated by assessing the features within a conjugate block on each of the input images. This matching statistic has traditionally been used as a standard method of assessing DEM surface reliability. To make the analysis easier, confidence levels were grouped into a number of classes (Table 1). However, there is no certainty that an excellent or good match as defined in Table 1 is actually a correct match, or that a correct elevation value is being returned. Similarly, there is a chance that isolated or suspicious cells were actually matched correctly, returning accurate elevations. Therefore this study investigates a better way to assess the elevation reliability of DEMs.

Table 1. Matching statistic correlation groupings used in this study

3.2. Failure warning model

In response to the limitations of the matching statistic method, Gooch and Chandler (2001) developed a more robust method of determining DEM surface reliability, which they called the ‘failure warning model’. This method used the sensitivity of individual DEM cells to changes in the DEM collection parameters, such as the search window size, the correlation size and coefficient limit. Two DEM surfaces collected using different parameters were subtracted from one another to produce a DEM of difference. Two reliability tests were used in the FWM. Firstly, any cell in the DEM of difference that returned a value higher than a 1 m threshold was flagged as unreliable. Secondly, cells interpolated during matching and located in regions of high slope angle were also flagged as unreliable. No indication is given in the original publication of what would constitute a steep slope. However, it seems that this should be linked to the nature of the topography of each study site (personal communication from M. Gooch, 2003). The rationale for the slope threshold of the FWM is that many studies have outlined the difficulty of obtaining reliable stereo matches in regions of steep slopes (Lane and others, 1994; Gooch and others, 1999). Thus use of the FWM method requires two raw input DEMs, and a slope map generated from one of the raw DEMs.

By changing the collection parameters, any number of DEMs can be derived. We collected 15 DEMs for austre Brøggerbreen and a FWM was calculated for each with the same base DEM. The results of these FWM runs are summarized in Table 2.

Table 2. Percentage of cells in each matching statistic class before (1) and after (2) implementation of the FWM

In each FWM run, the number of cells in each of the matching statistic image classes was calculated before and after the FWM, allowing the performance of the two tests to be assessed. Output from the FWM (e.g. Fig. 2) helps the operator identify the most reliable parts of the DEM by masking out regions that have failed one or both of the reliability tests. In this example, it is clear that the most unreliable parts of the DEM are the steep mountain slopes and the regions of deep shadowing. Both of these features are known to pose significant difficulties for stereo-matching algorithms (Gooch and others, 1999; Lane and others, 2000). Encouragingly, the forefield and the glacier appear to be reliable. Around 30% of the cells which the statistic image classed as an excellent match have been rejected by the FWM. Moving through the other class distinctions, on average around 50% of the good cells, 60% of the fair cells and 70% of the suspicious cells were flagged as potentially unreliable by the FWM. It is concerning that such a significant percentage (30%) of the cells matched to the highest confidence were removed by the FWM, and this result casts doubt over the suitability of the matching statistic image for assessing DEM surface reliability.

Fig. 2. An example output from the FWM: light grey indicates cells that failed both elevation and slope tests, dark grey those that failed elevation but passed slope tests, and black those that passed elevation but failed the slope test. Areas where the aerial photograph is visible have passed both tests.

However, Table 2 also shows that the total number of cells classed as unreliable by each run of the FWM can be as low as 37% or as high as 68.5%. This is a considerable variation but only represents 14 runs of the FWM. With the 15 DEMs it is possible to have 105 different runs of the FWM. These 105 runs are summarized in Figure 3. It is clear from Figure 3 that the number of cells identified by each FWM varies considerably, so care would have to be exercised when choosing the collection parameters for each of the input DEMs.

Fig. 3. Graph showing the number of cells removed in each of the 105 possible runs of the FWM.

3.3. Multiple input failure warning model

The sensitivity of the FWM method to the collection parameters forms the basis of its methodology, but it may also prevent the method being used to its full potential. To overcome the FWM’s shortfalls, we propose a new method, the ‘multiple input failure warning model’ (MIFWM). The basis of the MIFWM is to use multiple input DEMs (in this case the 15 DEMs) at the same time so that the sensitivity of the surface to all the collection parameters can then be used effectively. The MIFWM is based on the calculation of the variance of each DEM cell which is defined as

(1)

where σ ² is the variance of a cell, Z _c is the elevation of a cell in one particular DEM run, Z _m is the mean elevation of the cell for all DEM runs, and n is the number of input DEMs. Using this approach, it is possible to set a variance threshold value that determines whether a cell is classed as reliable or unreliable.

Table 3 shows that as the variance threshold is decreased, the number of cells that fail the MIFWM increases. However, it is useful to see the geographical distribution of cells that pass or fail the MIFWM at different threshold levels. Figure 4 shows the effect of altering the variance threshold level over the study area. Regions of shadowing that fall on steep slopes return the highest variance values. The shadowed areas of the forefield and the illuminated mountain sides are removed as the threshold level approaches 10 m (Fig. 4e). It is only as the variance threshold level is decreased to <5m (Fig. 4f) that significant areas of the forefield are flagged as unreliable.

Fig. 4. Binary output from the MIFWM for the study area generated using a number of different variance thresholds. Areas that are black have been masked as failing the variance test as described in the text. We use a threshold of 1 m, which masks 73% of the total DEM cells as unreliable, but only 34% of those cells on the glacier surface.

Table 3. Number of cells removed during each run of the MIFWM

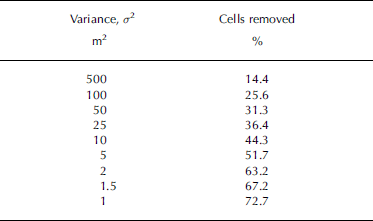
In this study, a variance threshold of 1 mwas used, and this flagged as unreliable almost 73% of the DEM cells (Table 3). This is a significant portion of the DEM cells. However, it is apparent that most of the glacier surface has passed the MIFWM threshold and is considered reliable (Fig. 4h).

4. Suitability of the Technique for Glacier Surface Monitoring

The primary purpose of this investigation was to determine the reliability of DEM surfaces in order to calculate the longterm surface change of glaciers. From a simple visual inspection, it appears that the MIFWM identifies significantly more unreliable cells in the glacier foreland than on the glacier surface (Fig. 4). Just over a third of the cells on the glacier surface were identified as being unreliable using the MIFWM technique (Table 4). If this analysis is extended to compare the performance of the other reliability tests that have been presented, then it is apparent that the MIFWM method actually identifies fewer unreliable cells on the glacier surface than either the statistic image or the original FWM (Table 4).

Table 4. Breakdown of cells removed across the glacier surface for the three data quality indicator methods. The glacier surface comprised 89 452 cells

Figure 5 presents the difference DEM for austre Brøggerbreen between 1970 and 1990. Areas that fail the MIFWM are masked out, together with those areas where the calculated height change is less than the combined error in the difference DEM, ±8m (Fig. 5). Errors in each individual DEM were calculated as the standard error of the difference between the modelled surface (DEM) and ground-truth data. The difference DEM is dominated by glacial retreat of ~550m and thinning of 0–50m over almost the entire glacier. Maximum thinning of ~50m occurs at the location of the ice terminus in 1990 (Fig. 5b). Regions just up-glacier of this have typically thinned by 30–40 m, which is an annual thinning rate of 1.5–2.0ma^–1 if this is assumed to be uniform over time. The frontal retreat is ~28ma^–1. In order to compare these results with those measured using conventional techniques, the whole area of the glacier was divided into 50m contour bands. The average thinning in each 50m band was then assigned to all pixels in that band, and the total mass loss calculated assuming a density for the volume lost of 0.91 kgm^–3 (i.e. ice). Over the entire surface of austre Brøggerbreen the lowering is equivalent to an annual balance of –1.06±0.3ma^–1w.e. This balance is higher than that calculated using traditional methods, –0.45±0.32ma^–1w.e. (Lefauconnier and others, 1999), but within error estimates. Other studies have also suggested traditional field-based methods may underestimate mass loss from glaciers, perhaps because stakes melt into the surface, resulting in an overestimate of accumulation (Braithwaite, 2002; Rippin and others, 2003).

Fig. 5. (a) Difference DEM showing surface lowering between 1970 and 1990. Background is low-resolution DEM. Cells that fail the MIFWM or where the difference is less than the combined error have been masked out. Solid line is glacier boundary in 1970; dashed line shows boundary in 1990. (b) Centre-line transect up-glacier through difference DEM. The glacier front in 1990 is at the dashed line between regions A and B.

5. Conclusions

Defining the reliability and accuracy of a DEM surface can be difficult, especially when the environment includes areas of high slope angle and deep shadowing. Collecting ground-truth data allows the user to be sure that the modelled surface represents the actual ground surface. However, the use of archived photogrammetry in a highly dynamic topographic setting such as the surface of a mountain glacier or a glacial forefield reduces the effectiveness of ground-truth data.

It has been shown that the statistical confidence of matching may not be a good indicator of surface reliability. Alternative techniques such as the FWM of Gooch and Chandler (2001) exploit the sensitivity of each DEM cell to subtle changes in the collection parameters in order to provide an indication of surface reliability. This method appears to be effective and can save the photogrammetrist considerable time. However, we show that the number of cells identified as potentially unreliable can vary by over 30% depending on the choice of parameters used to generate the two input DEMs. To fully utilize the FWM, the operator must understand and appreciate the effect of altering each collection parameter.

The development of the MIFWM addresses these shortcomings of the FWM and exploits all the collection parameters, thus truly testing the sensitivity of the surface to the collection parameters. The geographical distribution of reliable cells can be investigated easily and allows the operator to assess the fitness for purpose of the DEM. When applied to the mountain glacier study area, the MIFWM identified more cells as unreliable over the entire DEM, but fewer over the actual glacier surface, than the FWM technique.

Overall, the MIFWM is a more robust test of surface reliability than either the statistical confidence of matching or the FWM. It seems well suited to determining the reliability of DEM surfaces generated from archived images where ground-truth data may be sparse.