Determining the floe-size distribution of East Antarctic sea ice from digital aerial photographs

Abstract

Floe size within the Antarctic pack ice is an important parameter that affects both the ocean-ice-atmosphere energy exchange and the mechanical properties of pack ice. In this paper we present a computer-based algorithm to extract floe-size distribution information from digital aerial photographs of Antarctic sea ice. The algorithm segments digital images of sea ice into distinct floes from which the size of each floe is calculated and floe-size distributions are derived. Through a recursive application of the morphological erosion operator, each floe is eroded towards its centre while each pixel’s erosion number is recorded. This ensures no information is lost while individual floes are identified. The algorithm combines image-processing techniques with some manual input to accurately identify the boundaries of individual floes within an image. To demonstrate the functionality of the algorithm, six images, representing regions along a 22 km south-to-north transect through a transitional zone of pack ice near 65° S, 140° E, have been processed. Regional variations in the floe-size distributions show an increase in the number of smaller floes relative to larger floes and a decrease in the dominant floe size (in terms of areal coverage) from south to north. These results are consistent with ship-based observations.

Introduction

The Antarctic sea-ice zone is a highly dynamic environment, which causes the sea ice to be broken up into discrete floes. In the absence of any mechanical forcing, the surface of the ocean would freeze into a uniform sheet of sea ice, with a thickness determined solely by thermodynamic processes. Modelling studies (e.g. Wu and others, 2001) indicate that a thermodynamics-only scenario would result in much thicker ice than is presently observed. Hence, sea-ice dynamics and the creation and deformation of floes are fundamentally important processes within the Antarctic sea-ice zone.

The break-up of the sea ice into discrete floes is determined by stress and strain within the pack ice, including the effects of ocean swell, and the floe-size distribution is determined by the thickness and strength of the ice and the characteristics of the external forcing. The differential drift of floes will result in divergence or convergence of the pack and a resultant change in the thickness distribution. Thus, a complicated feedback develops as the floe-size distribution both affects and is affected by many other characteristics of the pack ice.

To accurately determine the floe-size distribution of a particular region, some form of aerial or satellite-based imagery must be processed. In this paper we present a new algorithm for processing aerial photographs of the Antarctic pack ice and compare the algorithm’s output with both the original images and manually segmented versions of each image. The algorithm is then applied to a set of six images of late-winter pack ice near 65° S, 140° E to quantify regional variability in floe-size distributions across a transitional zone within the pack. This transitional zone was chosen from aerial observations to represent a wide range of floe sizes.

Background

To calculate the floe-size distributions from digital images (satellite, aerial or otherwise) it is necessary to identify individual floes and estimate their size. Numerous approaches to this problem have been investigated (e.g. Rothrock and Thorndike, 1984; Banfield and Raftery, 1992; Burns and others, 1992; Korsnes, 1993; Muramoto and others, 1993; Lindsay and Rothrock, 1995; Soh and others, 1998), and in each study the approach taken was dependent on the source data, particularly its resolution. Of these authors, Banfield and Raftery (1992), Burns and others (1992) and Soh and others (1998) have extracted floe-size distributions from digital images through either automatic or mostly automatic procedures. The erosion-expansion (EE) algorithm presented in this paper is based on the algorithm of Banfield and Raftery (1992) but with significant alterations, and takes a similar approach to that of Soh and others’ (1998) restricted-growing algorithm. The EE algorithm improves on the algorithm of Banfield and Raftery (1992) in its ability to retain the actual sizes and shapes of floes, and in its ability to identify smaller floes.

Floe size can be defined in a number of ways (e.g. the area of the floe, the diameter of the largest inscribed circle, the mean of all diameters across the floe (mean calliper diameter), or the perimeter of the floe (Rothrock and Thorndike, 1984)). As our research employs a computer-based technique to process digital images, we use the number of pixels that make up a floe to define the size of a floe. Since the resolution of each image is known, this approach allows the approximate area of each floe to be easily calculated.

Once the sizes of floes have been calculated, there are two approaches for displaying and analyzing a floe-size distribution, namely a fractional-area distribution and a number-density distribution (Rothrock and Thorndike, 1984; Burns and others, 1992; Lindsay and Rothrock, 1995). The number-density distribution expresses the total number of floes within a size range (usually the bin size in a histogram) as a fraction of the total number of floes in the image. The usefulness of the number-density distribution may be limited, as the information relating to the spatial density of floes has been lost (Rothrock and Thorndike, 1984). The fractional-area distribution is similar to the number-density distribution but weights the floes according to their size. This distribution gives the area of all floes within a size range as a fraction of the area covered by the image. The fractional-area distribution gives a clearer indication of the distribution of floe size than the number-density distribution, but a spatially restricted sample space may increase the significance of large floes (Lindsay and Rothrock, 1995). More involved discussions on the number-density distribution and the fractional-area distribution, including formal definitions, are provided by Rothrock and Thorndike (1984) and Burns and others (1992).

Partially sampled floes (i.e. floes that are intersected by the edge of an image) complicate image processing. One approach is to include the partially sampled floes in a floe-size distribution to increase the sample size, but one cannot recover the actual size of such floes. In this paper we disregard the partially sampled floes that are identified in the south-to-north transect, in an effort to reduce the bias from our analysis of the transect.

A floe-size distribution generated from each image may be approximated by a mathematical function, providing a useful and robust method for comparing changes in floe-size distributions. The two functions proposed here are a power law and an exponential function (Rothrock and Thorndike, 1984; Lindsay and Rothrock, 1995). We may expect the coefficients and indices from these functions to relate to the properties of the sea ice; however, this is not investigated in this paper.

Methods

The algorithm for identifying sea-ice floes follows Banfield and Raftery (1992) and involves a two-stage process: segmentation of an image with an erosion algorithm, followed by re-creation of the original floe boundaries. Once individual floes have been identified, floe sizes can be calculated and the two floe-size distributions described above can be produced.

Our EE algorithm first requires a binary (black and white) image, where white represents thick ice (referred to as ice) and black represents new ice or open water (referred to as water), and a number of erosions to apply to the binary image. At present, the binary image is produced by applying a simple threshold to the original image at a given grey level. This means that all pixels with a grey level greater than or equal to the threshold grey level will be classified as ice (white), and all other pixels classified as water (black). The threshold level may be chosen either manually or automatically. The number of iterated morphological erosions to apply to the image is chosen manually and, apart from the threshold level which is optional, is the only manual input required. The EE algorithm iteratively erodes the binary image to a state where each remaining region of white pixels (ice) is considered to be a distinct floe. Thus, it is important that the number of erosions is chosen such that the leads and cracks are sufficiently opened to separate the surrounding floes, while the growth of any "holes" formed at the thresholding stage is restricted. "Holes" may form as a result of incorrectly classifying ice as open water (e.g. in the shadow of a ridge). While the growth of the "holes" themselves may not greatly affect the sizes of the floes, a "hole" grown during the erosion stage may split a floe in two. "Holes" may be overcome by choosing a lower threshold value, such that a greater range of dark pixels is changed to white (ice). For our images, which have ∼90% of grey-scale values between 30 and 100, a typical value for the threshold is around 50, and a typical number of iterative erosions is 15−20. Figure 1 shows the result of iteratively applying the morphological erosion operator to a binary version of a test image. The various regions of black (new ice/open water) can be seen expanding into the white regions (thick ice) such that closely spaced floes are eventually separated and leads and cracks are opened.

Fig. 1. The effect of the morphological erosion operator on a binary image, where white represents ice and black represents water, (a) binary image; (b) 5 erosions; (c) 10 erosions; ( d) 15 erosions.

The EE algorithm begins by iteratively applying the morphological erosion operator to the binary image a specified number of times. At each step, each pixel that is eroded (changed from white to black) has its erosion number recorded (e.g. 3 for the third iteration). This is an important element of the EE algorithm, as it allows the binary image to be later "regrown", step by step, to the image’s exact starting state. The erosion part of the algorithm is complete when the required number of erosions have been applied to the binary image.

The expansion part of the algorithm is then applied. This takes the eroded binary image and the information relating each eroded pixel to its erosion number and recreates the original binary image with each distinct floe individually identified. As it is presumed that the fully eroded version of the binary image contains distinct floes, the remaining regions of white pixels (thick ice) are identified and allocated a unique floe number. The eroded image is then recreated, step by step, back to its initial state. At each step this time, the pixels eroded at that step are included back into the image. For each of these pixels: if there is one and only one floe represented in the pixel’s 8−pixel neighbourhood then the pixel is associated with that floe (by assigning that floe number to the pixel); if there is more than one floe represented in the pixel’s 8−pixel neighbourhood then the pixel is associated with the floe with the greatest representation in the neighbourhood (or by a random choice between floes if two or more floes are equally represented); if no floes are represented in the pixel’s 8−pixel neighbourhood then nothing happens for the moment. This procedure is repeated until no more of the pixels are associated with existing floes. Any pixels that remain must represent floes that were fully eroded and have just come back into existence at this expansion step. As such, each group of these remaining pixels is identified as a distinct floe and is assigned a unique floe number. This process continues through each expansion step until the binary image has been recreated. At this time the image has been segmented into distinct floes based on the initial selection of the number of iterative erosions to apply to the binary image. This completes the expansion part of the EE algorithm. From the resulting segmented binary image, where each pixel has an associated floe number, it is an easy process to extract exact floe sizes and calculate a floe-size distribution for the image.

The algorithm is written in Interactive Data Language (IDL) with some Fortran and takes 1.5−3 min to fully process a 1536 x1024 pixel image.

Verification of the EE Algorithm and Discussion

We verify the validity of the EE algorithm by applying it to two different images of Antarctic pack ice, a (1536×1025 pixels; Fig. 2a) and b (subset of a full image, 770 × 566 pixels; Fig. 3a) and compare the results with manually segmented versions of the same images. The two images were obtained during a helicopter flight in August 1995 over a region of Antarctic pack ice near 65° S, 140° E. Both images were captured from an altitude of 1500 m looking straight down, giving each image a resolution of 0.47 m. Each image shows different ice conditions, with a displaying many closely packed floes with no one or two floes dominating the scene with their size, and b displaying generally distinct floes of similar size and one larger floe dominating.

Fig. 2. Test image a (1536 × 1024 pixels, 720 m × 480 m): (a) the original image; ( b) the ee segmented version; (c) the manually segmented version; ( d) comparison of the number-density distributions of both the ee and manual segmentation versions (bin size = 4.7m = 10 pixels); (e) comparison of the fractional-area distributions of both the ee and manual segmentation version (bin size = 4.7 m = 10pixels). the diamonds represent thefloe-size distributions of the manually segmented versions, and the squares represent thefloe-size distributions of the ee segmented versions.

Fig. 3. Same as for figure 2 but for test image b (770 × 566 pixels, 360 m × 266 m).

Threshold values of 50 for a and 51 for b were chosen to minimize the occurrence and size of shadows from both ridges and high freeboard floes, and to maximize the amount of new ice classified as open water. The number of erosion-propagations for each image (17 for a and 11 for b) was chosen to produce correct separation between floes. Each image presented in this paper was processed individually but with these same considerations.

Figures 2b and 3b show the results from the EE algorithm. Each shade of grey simply represents a floe identified by the algorithm. These results can be compared to both the original images (Figs 2a and 3a) and the manually segmented versions of the original images (Figs 2c and 3c). The majority of floes are accurately identified in both segmented versions for each image. Some differences are noticeable, however, and these mainly stem from ambiguities associated with defining a floe boundary. Tracing around each floe by hand created the manually segmented versions. To discriminate floe boundaries we applied a rule of thumb that "if one can walk from point A to point B then both A and B are on the same floe". To ensure an objective comparison, we performed the manual segmentation of the images before processing them with the EE algorithm. In Figures 2d and e and 3d and e the × axis is expressed in terms of the "effective floe width" (the square root of the floe area) to create a non-linear distribution of floe widths. All of the floes identified (partially and fully sampled) have been included in these analyses, as we are more interested in this section in the algorithm’s ability to identify floes than in the resulting floe-size distribution. A power law has been applied to the number-density distributions, and an exponential function to the fractional-area distributions. The similarity of the resulting best-fit functions verifies the ability of the EE algorithm to segment an image into individual floes and to accurately identify the boundaries of those floes.

The sensitivity of the algorithm to the threshold value and number of erosions was also investigated. The results of processing the two test images with (a) different thresholds for a constant erosion number, and (b) different erosion numbers for a constant threshold, were analyzed. The chosen values for the threshold and the number of erosions for each image were taken as the constants; hence, we investigated the sensitivity of the variables about our chosen optimal values. Few differences were observed between the results for each image, and no trends were apparent. This indicates that although user input is important for an accurate floe-size distribution, the particular values chosen for the threshold and number of erosions are not critical provided they are close to the optimal values.

In summary, the comparisons in Figures 2 and 3 show that the EE algorithm successfully extracts discrete floes and floe-size distributions from digital aerial photographs. The main limitation of the algorithm at present is the thresholding stage where a single threshold is required for the whole image. While the images cover only a relatively small area, anomalies in the pixel values due to ridge shadows, shadows from high freeboard floes and new ice can still cause cracks to be classified as thick ice, and shadows over ice to be classified as new ice/open water. The local dynamic thresholding technique described by Haverkamp and others (1995) and further used by Soh and others (1998) is an alternative option for creating a binary image that we are yet to investigate. The advantage of the EE algorithm is its ability to quickly and accurately identify each floe within a large image regardless of the floe’s size (down to the resolution of the image, i.e. 1 pixel or 0.2 m²). It is possible, however, that such small "floes-are not true floes but speckle in the image enhanced by the thresholding stage. As such, we use a minimum floe size of 9 pixels (3 × 3 pixels), or 2.0 m², in the analyses presented in the following section.

Results From the South-North Transect and Discussion

As an application for the algorithm, six images of East Antarctic pack ice have been processed and their floe-size distributions have been calculated. Each image was collected on 8 August 1995, and the series represents a 22 km south-north transect through a transition zone of pack ice between 64°38’ S, 139°54’ E and 64° 12’ S, 140° ll’E. Although this transect is short, the six images show a good range of floe sizes from large floes with diameters up to 250 m to small floes with diameters around 5 m (visual estimate prior to processing). These six images, from south to north, are referred to as images c-h. Each image has the same spatial dimensions and resolution as test image a, i.e. 1536 x1024 pixels (720 m × 480 m) with a resolution of 0.47 m.

Table 1 gives the distance from the ice edge, the user-defined variables, the number of floes identified and the ice concentration for each image. Figures 4–6, respectively display from south (C) to north (h) each original image, the number-density distribution for each image, and the fractional-area distribution for each image. The threshold and iteration values for images g and h were particularly difficult to choose as the sea ice was faintly illuminated and consisted of densely packed floes. Three of these images (d, f, h) have been analyzed manually by Lytle and others (1996) to assess the effect of floe size on SAR imagery. They calculated average floe widths from the floe area assuming round floes. After adjusting for this, they report average floe widths of 88,17 and <9 m for d, f and h, respectively. This compares to our average floe widths of 19, 13 and 9 m, respectively, as calculated for the fully sampled floes only with a minimum floe area of 9 pixels. As such, our average floe widths are less as we did not count the large floes that are partially sampled, while Lytle and others (1996) did not include many of the smaller floes (personal communication from V. Lytle, 2000). This is particularly evident in the comparison between average floe widths for image d.

Table 1. A list of all the images in the south-to-north transect, with their distance from the ice edge, values for the threshold and number of erosions applied, the number of floes identified (fully sampled floes only; minimum floe size of 9 pixels) and the ice concentration

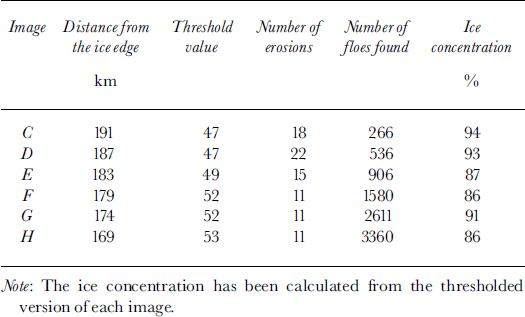
Fig. 4. The transect images from south (c) to north (h).

Fig. 5. The corresponding number-density distributions for each image in figure 4 (bin size = jo pixels = 4.7 m).

Fig. 6. The corresponding fractional-area distributions for each image in figure 4 (bin size = 10 pixels = 4.7m).

The floe-size distributions for each image have also been calculated from only the floes that were fully sampled by the algorithm. Hence we see floe widths no greater than around 130 m, and image c, which clearly has the greatest average floe size of the set of images, with a maximum floe width less than images d and e. This is due to the relatively small spatial coverage of the images with respect to the average floe size for each of the southern images. Power and exponential functions were fitted to each floe-size distribution. A power law was a consistently better fit for each number-density distribution, while exponential functions better described each fractional-area distribution (although the r² values for the exponentials are low for the southern images).

The regional variations in both the number-density distributions and the fractional-area distributions show interesting characteristics. Each number-density distribution in Figure 5 is approximated very well by a power law. Although the power functions themselves are not similar, trends can be seen in the coefficients (increasing rapidly) and indices (slowly decreasing). These trends suggest that as we move north towards the ice edge the numbers of smaller floes within a range of floe sizes (3×3 pixels to ∼80 × 8 0 pixels or 2 m² to ∼1400 m²) rapidly increase, while a significant contribution from relatively larger floes is maintained. In other words, we see an almost fractal behaviour of the pack as relative numbers of smaller and larger floes are maintained while the average floe size decreases towards the north.

The fractional-area distributions presented in Figure 6 also show an interesting trend, with the general slope of each dataset gradually decreasing from south to north. This change is reflected in the exponents of the fitted exponential functions. These exponents decrease from positive to zero to negative through the south-to-north transect, indicating continuous changes in the dominant floe size from large floes in the southern images to small floes in the northern images. This change in the dominant floe size is also well observed in the hourly ship-based observations conducted in the region. While these observations and trends are suggested in a qualitative sense by the original images, and are intuitive to some degree, it is comforting for them to be replicated in these results from a 22 km transect through a transition zone of pack ice. Further investigations are underway to analyze longer transects involving a greater number of images in other regions of East Antarctic pack ice.

Conclusion

Floe-size distribution is an important parameter for defining the character of the Antarctic pack ice, and a new technique for determining this from digital aerial photographs has been presented. The algorithm used in this method represents an almost completely automated method for processing digital images of sea ice, and produces both fractional-area and number-density distributions of floe size. The results from a number of different test images, and comparisons with manually processed images, show that the algorithm accurately identifies and calculates the area of floes within the image. Ambiguities in the definition of floe boundaries complicate the processing in some cases, and to resolve these the user is required to specify the number of erosion iterations that are performed. This, and an option to specify the threshold value used to create the binary image, are the only interactive elements of the algorithm.

A series of images along a south-to-north transect were processed and clearly showed spatial variability in the floe-size distribution that can occur through a transition zone of Antarctic pack ice. Such a zone may represent the limit of swell penetration from a particular storm event, and clearly identifies a marked change in the character of the pack. Lytle and others (1996) showed from a subset of these images that variations in floe size affected the backscatter values in synthetic aperture radar (SAR) imagery and qualitatively segmented near-coincident SAR imagery into distinct backscatter zones based on floe size. The research presented in this paper indicates that we will now be able to apply a quantitative measure of floe size to further assess the effects of floe size on SAR and other satellite imagery.