Experimental study on the micro-fabric of frozen sediment using triaxial deformation and computerized tomography

Abstract

The micro-fabric of frozen sediment was studied using a triaxial deformation machine with computerized tomography (CT) to describe a quantitative relationship between microstructure and mechanical behaviour at different temperatures and confining pressures. Micro-fabric changes were described by CT images and CTvalues. Relationships between CT values and the stress–strain curves were analyzed. It was shown that CTvalues can describe the deformation quantitatively.

Introduction

The mechanical behaviour of frozen sediments is one of the key issues for understanding glacial flow (Boulton and Dobbie, 1993). The microstructure of frozen sediments plays an important role in their mechanical properties. As shown in Gong and others (2000), both stress–strain and pore-water-pressure–strain relationships for saturated soil are closely related to fabrics. Soil fabric depends on the soil’s density, granularity and moisture and reflects its mechanical behaviour. For example, the void volume in loess is related to its collapsive property, and the orientation of particles in clayey soil is related to its anisotropic mechanical properties. The fabric of frozen soil is closely related to its temperature and water content due to a phase transformation of water, which affects the arrangement and linkage among soil particles.

Optical and electronic microscopes have been used to analyze the micro-fabric of frozen sediments (Chamberlain and Gow, 1979; Pusch, 1979; Konrad, 1989), but many of these studies were focused on the freeze–thaw process and its influence on the soil fabric. It was found that freeze–thaw changes the soil fabric, which leads to changes in both the physical and mechanical properties of soils.

In recent years, computerized tomography (CT) has been widely used in geo-engineering studies (Tollner and Verma, 1989; Homem and others, 1999; Alshibli and others, 2000; Ren and others, 2000). CT has two main advantages over the microscope as a means of describing the microstructure. Thefirst is that information on the internal fabric of specimens can be obtained quantitatively and dynamically without damaging the specimen during the experimental process; the second is that three-dimensional images can be obtained and there is no overlap in images. In previous studies, the failure progress was described and discussed. The CT technique proved effective in detecting internal fabric, inhomogeneities, localization patterns, and quantifying void ratio variation within specimens, but little work has been carried out on frozen soil. Wu and Ma (1994) studied fabric change during the uniaxial creep process of frozen soil and found that fracture was initiated from micro-fissures and other structural defects during deformation of frozen soil.

Besides soil particles, the fabric of frozen soil is related to interstitial ice and unfrozen water. The average density, which characterizes the distribution of particles, ice and unfrozen water across a specimen section, is described by the CT value as defined in the following formula (Siemens AG, 1991):

where μⁱ denotes the absorption index of the target, and μ^H2O denotes the absorption index of pure water. The unit of CT value is HU (Hounsfield unit).

In this paper, we aim to find a quantitative relationship between the mechanical behaviour and microstructure change in frozen soils by CTscanning.

Preparation of Samples and Test Process

The material used in the test was a loess soil from Lanzhou, China. The specimens were remoulded and cylindrical, being 61.8 mm in diameter and 150 mm in length. The water content and bulk density were 2 2% and 1.6 gcm–₃, respectively. We prepared the samples in an unfrozen state using an automatic sampling device, then froze them in a fixed mould to prevent freezing dilation and to avoid changing their dry density. The prepared frozen samples were stored in a freezer at their testing temperatures.

A Siemens-Somaton Plus X-ray horizontal CT machine (Siemens Company, Germany) with a spatial resolution of 0.12 mm₃ and a density comparison resolution of 0.3% (3 HU) was used in conjunction with a dedicated low-temperature triaxial deformation machine.

Tests were carried out at –5° and –10°C. At each temperature, four confining pressures, a₃ = 0, 1, 2 and 3 MPa, were applied. For the confining pressure of 0 MPa, we did not apply any cell pressure; there was only cooling liquid around the sample. Before every test, the temperature of the liquid in the pressure cell was lowered. Then a frozen specimen was taken from the freezer and installed in the cell, and the cell temperature was stabilized. The deformation strain rate was 0.00133 min^–1 in the whole series. The specimen was scanned before the application of axial pressure to produce a reference CT image and CT value.

During deformation, we scanned the specimen at strain stages of 2%, 5%, 8%,10%,12% and 13%. For each stage, five sections, each 5 mm thick, were scanned. We took care to locate the position of each section in the specimen taking into account specimen deformation, so that the same target section was scanned at every strain stage. The stress–strain data were recorded together with the CTscans.

Results Analysis and Discussion

Every point within a section can yield a CT value, but we could not focus on every point since not every point can be located precisely when the specimen deforms, and the randomness of the CT value for a point is too large. Any particular point in the specimen cannot be related to the specimen stress–strain behaviour, but the average of all points in all five sections is related. Then we obtained an average CT value of the five sections in the specimen at a certain strain stage. Our analysis focused on mechanical behaviour of the specimen and this CT value.

Figure 1 shows the failure process of the specimens at –5°C and a₃ = 0 and 3 MPa, respectively. When unconfined, damage started from the centre of the specimen, then expanded to the sides until fractures appeared on the wall (see Fig. 1a). At all strain stages, the damage gradually evolved. By contrast, upon increase of the deformation at a₃ = 3 MPa, the holes in the specimen gradually closed (see Fig. 1b). For the specimens at –5°C and a₃ = 1 and 2 MPa, the same phenomenon was observed as at a₃ = 3 MPa. Therefore, for the specimen under unconfined compression (a₃ = 0 MPa), the deformation was of dilation type, while for the specimen under a confining pressure ≥ 1 MPa, it was of densification type. This was also the case for samples analyzed at –10°C.

Fig. 1. CTimages of specimens at two confining pressures and at a temperature of –5°C. (Deformation increases left to right, top to bottom.) (a) σ3 = 0 MPa (unconfined); the damage starts from the centre of the specimen, and the damage zone expands to the sides. The fractures ultimately appear on the walls. (b) σ3 = 3 MPa; with the increase of deformation, the holes in the specimen gradually close.

From the stress–strain curves in Figure 2a and b, we find at both temperatures (–5° and–10°C) that whena₃ = 0 MPa the stress–strain curves all showed a softening shape. However, under confining pressures of 1, 2 and 3 MPa, the stress–strain curves all showed a hardening shape. Comparing the CT-value–strain curves with the stress–strain curves in Figure 2, we find a similarity in curve types, i.e. CT-value–strain curves have the same weakening or hardening shapes as the stress– strain curves under the same experimental conditions.

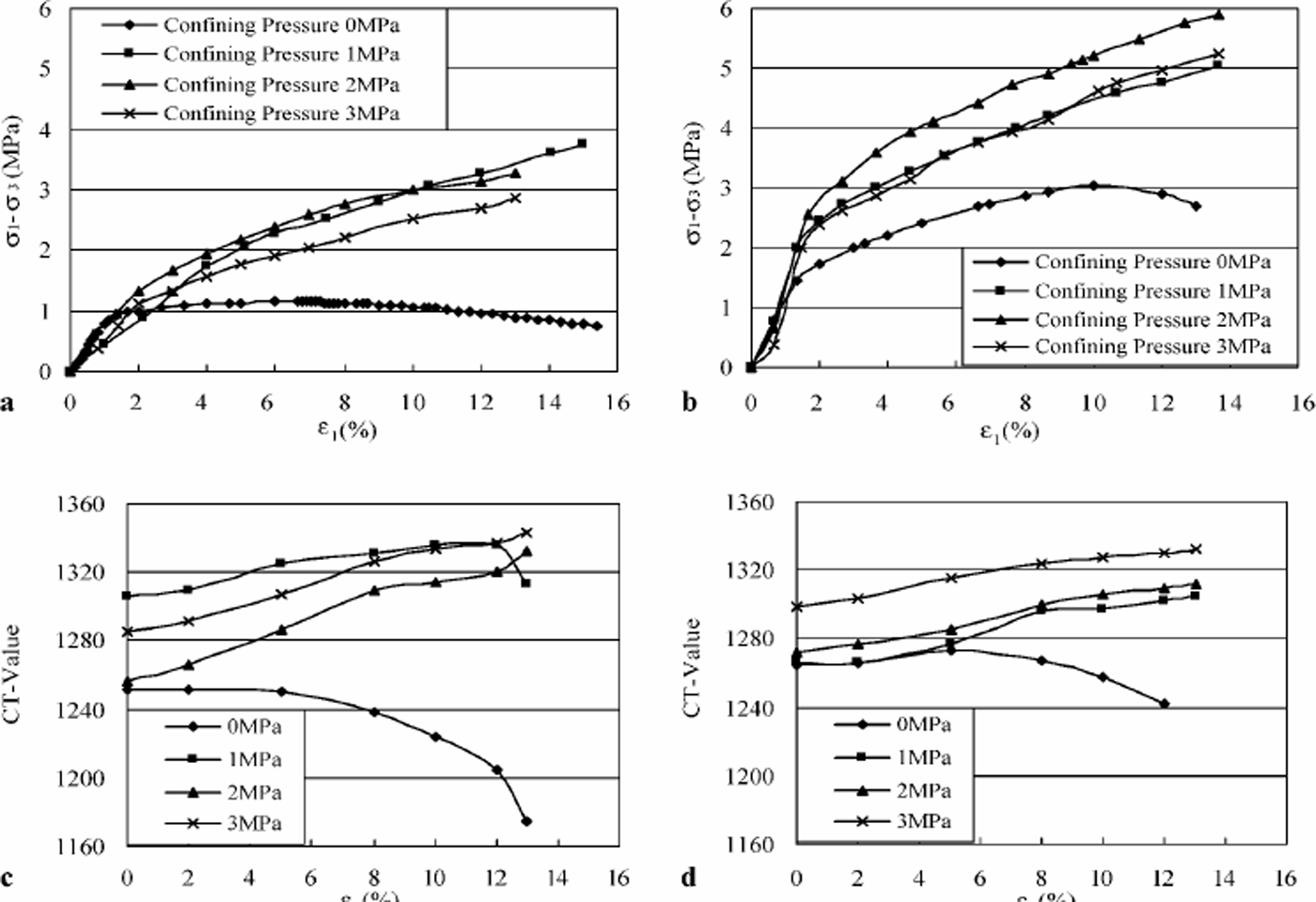
Fig. 2. Stress–strain curves and CT-valuestrain curves: (a, b) stress–strain curves at–5°C (a) and–10 C (b); (c, d) CT-values strain curves at –5°C (c) and –10 'C (d). CT-value–strain curves have the same softening or hardening shapes as stress– strain curves under the same experimental conditions, which is significant for describing the mechanical behaviour of frozen soil.

Based on the data presented in Table 1 and Figure 2a and c, we see that at –5°C and a₃ = 1 MPa the test produced an abnormally large initial CT value and high strength. For tests at CT₃ = 3 MPa, the data in Figure 2 show that at both temperatures the specimens had less strength than at 2 MPa. We believe that the high confining pressure damaged the original structure of the specimens, resulting in damage to the connection between particles, which was described by Ma and others (1999) as a weakening function of the confining pressure. Table 1 shows that at –5° and –10°C when a₃ = 3 MPa, the original CT values increase more rapidly than at lower confining pressures. This to some extent reveals this phenomenon quantitatively. As with the relationship between the CT value and the strength of frozen sediments, further study is required considering the weakening function of confining pressure.

Table 1. Indexes and parameters of specimens used for tests

Conclusions

It is concluded that:

CT images can reflect deformation quantitatively for frozen soil;

the CTvalue can be used for quantitative description of frozen sediment fabric during deformation;

CT-value–strain curves change in the same way as stress–strain curves.

This is important for the development of a micro-fabric-based constitutive relationship for frozen soils.