Introduction
The polar ice sheets are major contributors to changes in global sea level. They are among the least explored major reservoirs of water on Earth and are very likely changing volume with time. The reason for the poor understanding of them is their very large size and the technical difficulty in measuring their state of balance. To date there is no precise assessment of the current behaviour of the ice sheets.
The advent of geodetic-quality global positioning system (GPS) survey methods opens the possibility of a direct and locally specific method of measuring mass balance with long-term significance. This method involves the comparison of the vertical component of velocity of markers set beneath the surface, as measured using GPS, with the long-term rate of snow accumulation, obtained from a firn core. The difference between vertical velocity and snow-accumulation cate is the local rate of ice-sheet thickening or thinning. The first results of this method, presented here, involve setting long poles into “coffee cans” at the bottom of deep holes. Newer versions of the method no longer use coffee cans, but it is still called the “coffee-can” method.
Very precise results can be obtained with the “coffec-can” method. An assessment of measurement uncertainties and their effect on the result indicates a net uncertainly of about 0.02 m a−1 thickness change over a 5 year observation interval (Reference Hulbe and WhillansHulbe and Whillans, 1994). With such long-term measurements, the biggest uncertainty is the accumulation rate; the uncertainty arises from the difficulty in measuring the profile of density above dated horizons. Lesser uncertainties derive from the correction for densilication beneath the markers and from the GPS surveys, where it is estimated that the uncertainty is a few mm a−1 (Reference MorganMorgan, 1994).
The “Coffee-CAN” Method
There are two parts to the “coffee-can” method. The first part relates to the determination of a vertical velocity, i, of a master station. The second part relates to the transfer of information from the master station to the local array which is used to ensure that the spatial terms are well determined as well as providing for spatial averaging and variability of local rates of change.
In both parts, markers are set at the bottom of vertical holes, usually 10-20 m deep. in the prototype set-ups, each marker is connected to a surveyablc point above the snow surface by a steel pipe (Fig 1). Latter set-ups use non-stretch-able steel cable. Static GPS surveying is done using dual-frequency receivers (Trimble 4000 series or Ashtech Z-12) to the master pole, during at least two field seasons to determine its vertical velocity. Kinematic GPS and optical levelling surveys connect the master station to other markers in the local array.
The vertical component of velocity, ż, is combined with other measurements to calculate the local rate of thickness change, Ḣ as follows:

Fig. 1. Schematic rif a "criffee -can" marker.
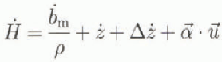
in which ![]() is accumulation rate (expressed as mass per unit area and time), ρ is the density at marker depth, and Δż is an adjustment if the marker is different from the master tracking site. Local surface slope,
is accumulation rate (expressed as mass per unit area and time), ρ is the density at marker depth, and Δż is an adjustment if the marker is different from the master tracking site. Local surface slope, ![]() , is considered positive in the down-grade direction. It is obtained by profiling the local terrain in various directions away from the site out to a distance of about 5 km using GPS. The slope over a horizontal scale, about equal to ice thickness (2 km), is assumed to be time-invariant. Horizontal velocity,
, is considered positive in the down-grade direction. It is obtained by profiling the local terrain in various directions away from the site out to a distance of about 5 km using GPS. The slope over a horizontal scale, about equal to ice thickness (2 km), is assumed to be time-invariant. Horizontal velocity, ![]() , is obtained from the repeated tracking of the marker pipes by GPS. The dot product of surface slope and horizontal motion is the correction for along-slope motion. That correction is small and relatively free of measurement uncertainties (~0.0004ma−1).
, is obtained from the repeated tracking of the marker pipes by GPS. The dot product of surface slope and horizontal motion is the correction for along-slope motion. That correction is small and relatively free of measurement uncertainties (~0.0004ma−1).
Accumulation rate, ![]() is obtained from dated horizons in firn cores and the depth-integrated density above that horizon. If a good-quality value for the site is not available from other work, accumulation rate is taken from the depth of measured nuclear-bomb fall-out. These levels are detected using measurements of gross beta activity, as described in Whillans and Bindschadler (1988). Densities are obtained from measurements conducted in the field immediately after core recovery. Core loss is assigned according to the scheme in Whillans and Bolzan (1988).
is obtained from dated horizons in firn cores and the depth-integrated density above that horizon. If a good-quality value for the site is not available from other work, accumulation rate is taken from the depth of measured nuclear-bomb fall-out. These levels are detected using measurements of gross beta activity, as described in Whillans and Bindschadler (1988). Densities are obtained from measurements conducted in the field immediately after core recovery. Core loss is assigned according to the scheme in Whillans and Bolzan (1988).
The time-scale of significance for the “coffee-can” results is limited by the time-span of the accumulation-rate value. in the present study, I hat span is 40 years, the age of buried nuclear bomb levels. This time-span is significant to discussions of the cause of changes in global sea level, which is considered at the 30-70 year time-scale (Reference Warrick, Oerlemans, Houghton, Jenkins and EphraumsWarrick and Oerlemans, 1990). However, this is not an intrinsic limitation. in principle, it is possible to recover longer cores and potentially obtain a longer-term accumulation rate.
The limitation of the “coffee-can” technique is that only point measurements of thickness change are obtained. The spatial representativity of the results musi be assessed by installing several sites, or by coordinating measurements with other methods. The ideal would be to combine the “coffee-can” method with other methods that have wider spatial significance, such as repeat laser altimetry. “CofTee-can” sites can serve as fiducial control on such studies. They can be used to link short-term fluctuations in snow-surface height to mass balance, and provide locally specific values that can be extrapolated over larger areas with laser altimetry.
The largest uncertainties in Equation (1) are those relating to the GPS determination of ![]() and the glaciological de-termination of
and the glaciological de-termination of ![]() . Uncertainties in
. Uncertainties in ![]() improve with increasing time-spans of observation. Uncertainties in the determination of bm
are limited by physical measurements of the core and are not improved with a longer record.
improve with increasing time-spans of observation. Uncertainties in the determination of bm
are limited by physical measurements of the core and are not improved with a longer record.
Gps Calculations
Marker positions are calculated using the GAMIT/ GLOBK software package (Reference HerringHerring, 1997; Reference King and BockKing and Bock, 1997). This package uses data from tracking stations around the world to compute orbits for the GPS satellites and precise positions for the stations. The tracking data come from the International GPS Service for Geodynamics (IGS), as well as other Southern Hemisphere tracking stations. Parameters solved for include the three coordinates of each station position, 13 tropospheric delay parameters for each station, 15 parameters for each satellite (six gravitational parameters and nine non-gravitational parameters of the BERNE model (Reference BeutlerBeutler and others, 1994)) and six parameters associated with the Earth's orientation. Extensive modelling was undertaken for solid Earth tides and the effects of receiver and satellite clocks. Corrections for antenna phase-center variation are made as appropriate for the antenna model (unpublished information from G. L, Mader and J.R. MacKay).
For data from 1992 and 1993 (table 1) a single global network of 28-30 stations is used, together with some other data from permanent trackers in Antarctica (Fig. 2). These additional regional data added stability to the solution.
The 1995 data (table 1) cannot be satisfactorily reduced in GAMIT, as they were sampled at 15 min intervals, compared to the 30 s sampling used in 1992,1993 and 1996.
Table 1. Calculation of rate of ice-thickness change

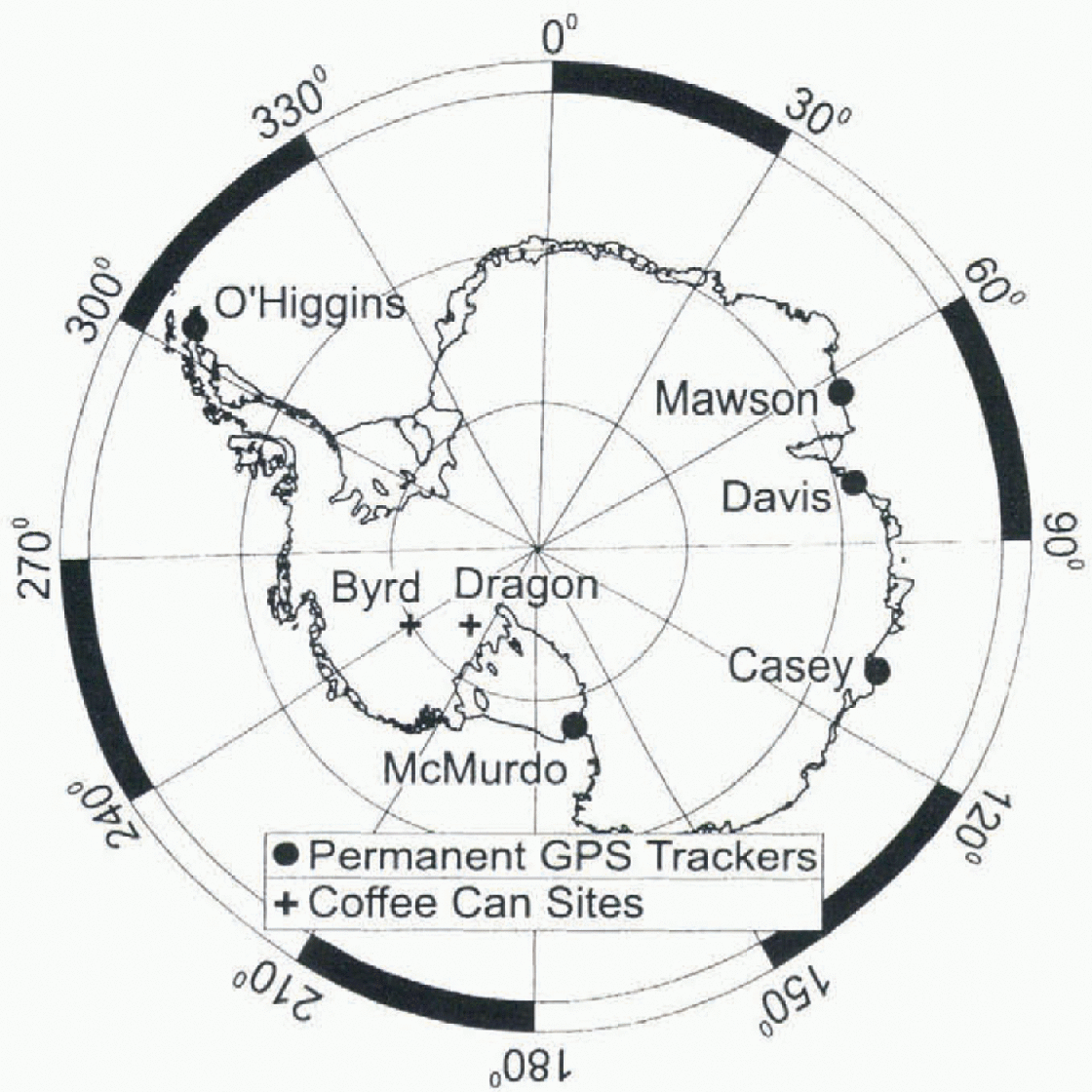
Fig. 2. Location map of Byrd and Dragon “coffee-can” sites and Antarctic permanent GPS sites.
For 1996 (table 1) two solutions are made. The first is a 12-station Southern Hemisphere solution, which includes the master reference poles DG37 and ORSP at the “coffee-can” sites. The second is a full global solution without these special poles. The first solution is, as noted below, folded onto the global solution utilising common stations so that all three epochs are referenced to the International Terrestrial Reference Frame, ITRF94, as determined by the International Harth Rotation Service.
At this point in the calculations, there are solutions available for each 24 h time period of satellite tracking. Some of the ice-sheet stations have several consecutive days of tracking, each of which has produced a solution for positions of the icc-shcct stations as well as for the seiet led global stations. These results, together with the full var-iance-covariance matrix of the daily solutions, are unified using the GLOBK package into a single consistent solution of positions and velocities of the stations. The velocities are constrained to be constant in time.
In the case of the 1996 data, two solutions, each with a full variance—covariance matrix, were used. The two solutions were reconciled by utilising the eight common stations and determining a common orbit. The procedure of computing regional and global networks is described in Morgan and others (1996). It conserves computational effort while providing better access to the global reference frame.
As a final step, the positions of some of the IGS stations are constrained using the GLORG software package. The nine IGS stations, whose positions are known to belter than lem at all relevant times according to the International Earth Rotation Service's reference system ITRF94, art-used. These stations are ALGO, FAIR, HART, KOSG, SANT, TIDB, TROMS, YARl and YELL, and are globally well distributed. The procedure results in a seven-parameter (three rotations, three translations and one scale) fit of GLOBK output to the ITRF frame. The adjustment in scale is 1-2 x 10−9 and so is insignificant, meaning that the adjustment is basically a rigid mapping of the coordinate systems. The result is positions and velocities of the icc-shcct stations tied to known positions and velocities around the globe.
Site Descriptions
Each site consists of a suite of five markers. The Byrd site is located 2 km east of Byrd Surface Camp (80°01'S, 119°28'W; Fig. 2). Its location is clear of any drift effects associated with Byrd Surface Camp and the former New Byrd Station.
The “Dragon” site is at the edge of an inter-stream ridge next to the shear margin to Ice Stream Β (83 45'S, 138°W; Fig. 2). This ridge, called the Unicorn, separates ice-stream tributaries Bib and B2. Horizontal velocities on the Unicorn are typically less than 2 m a−1 (Whillans and Reference Van der VeenVan der Veen, 1993). The ridge is bounded to the north, about 1 km north of the marker site, by a shear margin called the Dragon.
Results
Table 1 displays results from the master marker at each site. The results from the other markers are consistent (within 0.015 ma−1) except for one of the markers at the Dragon site, which is suspected of settling into drill chips left behind from the drilling. Local ice-sheet thinning is indicated for the Dragon site, whereas the Byrd site is close to balance.
Figure 3 shows the individual height determinations for the master marker DG37 at the Dragon site, and the variations in these determinations which impact on the determination of i. The quality of this mean value is improved by increasing the frequency of observations and their span. Reductions in individual uncertainty over time restili from an improved GPS constellation, a denser tracking network and longer occupation times.
Accumulation rates and horizontal velocities are consistent with earlier results. The velocity at the Dragon (measured as 1.98 (0.02) ma−1 to the northwest) is comparable with two earlier determinations. Whillans and Van der Veen (1993) used Transit satelliie surveys on station 21, which is 3 m away from DG37, and reported a velocity of 1.5 (0.4) m a−1 to the northwest. K. E. Echclmeyer (personal communication, 1995) obtained a velocity of 2.04 (0.04) m a−1 to the northwest from GPS tracking of DG37 between January 1994 and January 1995. Horizontal velocity at the Byrd site measured in this study is 11.83 (0.01) ma−1 to the southwest. This is comparable with earlier measurements of 11.5 m a−1 obtained in 1992 using GPS (U.S. Geological Survey, unpublished report) and 12.7 ma−1 from satellite Doppler fixes (W. H. Chapman, reported in Whillans, 1977), both towards the southwest. Accumulation rate measured at the Byrd silt-is 0.127 m a−1 (ice equivalent). This falls with in the range of values reported by Reference Langway, Osada, Clausen, Hammer, Shoji and MitaniLangway and others (1994) for two cores in the vicinity: 0.101 m a−1 from a 1350 year record obtained 1 km east-northeast of Byrd Surface Camp, and 0.127 m a−1 from a 40 year record at a site 14 km east-northeast of the Station, Some of the variations could be due to small differences in position of the measurements or to measurement uncertainties, but these differences are minor.
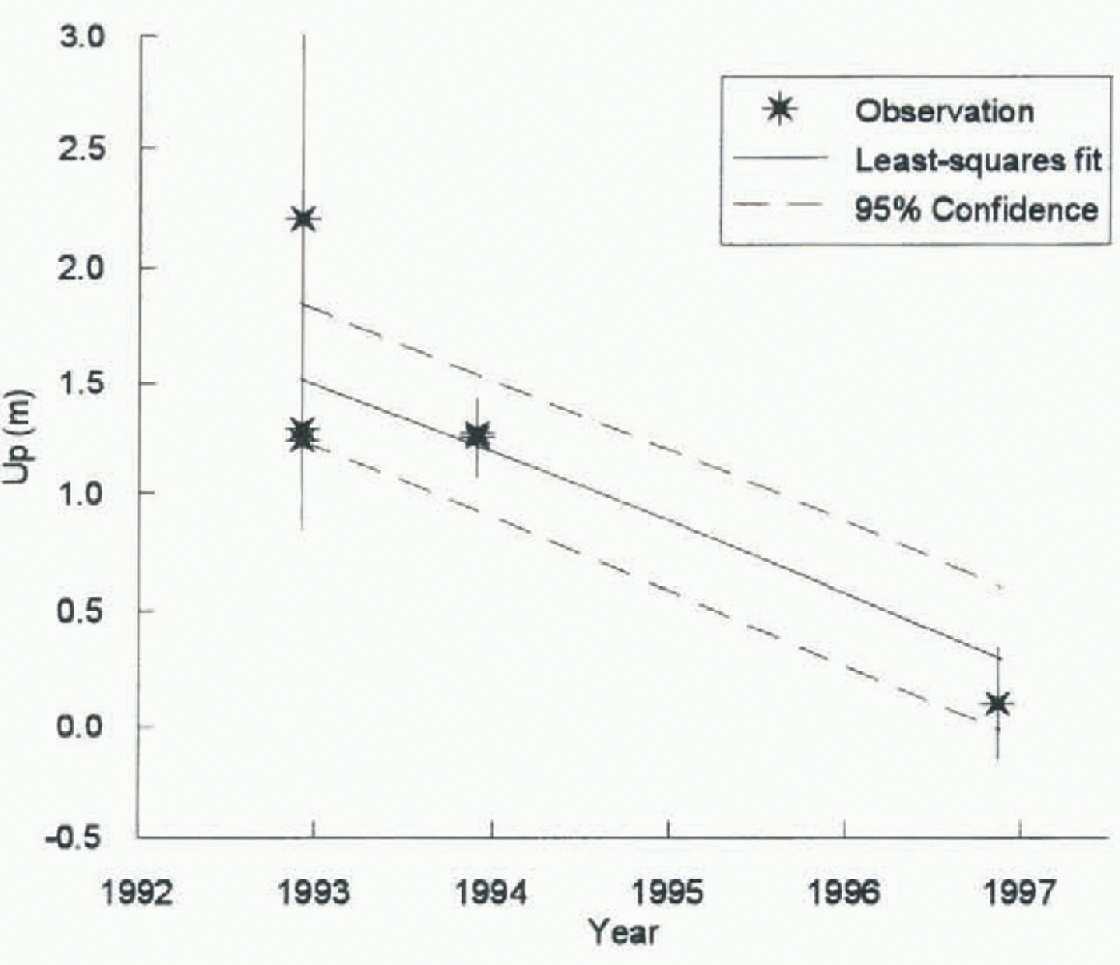
Fig. 3. Vertical motion of marker DG37. Horizontal axis tick marks are at 1 January of the year.
Other Evidence on Mass Balance at the Measured Sites
The thinning rate measured at the Dragon expands on other evidence of change. The inter-stream ice is being consumed by Ice Stream B. The evidence for this is that the hook-shaped crevasses at the outer edge oflhe shear margin are too straight to be accounted for by steady-stale kinetics. Their shape indicates a relative motion of the shear margin with respect to the ice of the inter-stream ridge that is faster than the measured motion of the ice from the inter-stream ridge. This indicates an ongoing southward migration of the shear margin (which is interpreted as widening of the ice stream). Very probably lhis southward migration and the thinning discovered here are mani lesta ι ions of a single overall process of evolution of the ice sheet in this region.
The calculations of shear-margin migration are as follows. The radius of curvature of the hook-shaped crevasses, is 100-400 m (Reference Vornberger and WhillansVornberger and Whillans, 1990). The lateral shear rate, ux,y, is 0.15 m a−1 (Whillans and others, 1993). These values are used in the formula
from Vornberger and Whillans (1990) that describes the bent crevasses in a zone of simple shear with translation perpendicular to the shear zone. Solving the formula for the rate, Uy , at which ridge ice flows across the outboard limit to the ice stream yields 7.5 30 m a−1. This is to be compared with the GPS-measured horizontal speed of about 2 m a−1. The différence between the crevasse-inferred speed and the GPS-inferred speed of 5-28 m a−1 indicates that the outboard limit to the ice si ream is migrating into the inter-stream ridge and that this migration is most probably-accompanied by thinning.
At Byrd Station, an earlier study found that the ice sheet is thinning at 0.03 m a−1 (Whillans, 1977). The present work obtains a consistent value. However, identical results are not to be expected. The earlier work applies to the region up-glacier of Byrd Station, whereas the present “coffcc-can” results apply just next to Byrd Station.
Other Techniques for Mass-Balance Determination
The conventional method for obtaining mass balance entails comparing the mass input by snow accumulation with horizontal discharge through a coastal gate (e.g. Reference Giovinetto and BentleyGiovinetto and Bentley, 1985; Whillans and Bindschadler, 1988). However, the propagation of measurement uncertainties leads to rather large uncertainties in the calculated results. in the case of Ice Stream B, the most thoroughly studied catchment, the uncertainty is 0.04 m a−1 in thickness change (Whillans and Bindschadler, 1988), a rather large uncertainty thai is limited by the ability to define the limits to the catchment area (Reference Price and WhillansPrice and Whillans, 1998) and by-spatial and secular variations in accumulation rate and the expense involved in adequately sampling it (Reference Venteris and WhillansVenteris and Whillans, 1998). The precision of the mass-balance estimate for the catchment of Ice Stream Β is slightly better than that obtained here, but without the potential for great improvement with a few more measurements as with the present method.
A second method is remote sensing of the snow surface by satellite radar or aircraft laser ranging. Repeat measurements provide the change in elevation of the snow surface or of subsurface reflectors over the time-span between measurement epochs. Each airborne laser mission provides elevations that are accurate to about 0.30 m (Reference Krabill, Thomas, Jezek, Kuivinen and ManizadeKrabill and others, 1995). Mass balance is obtained from repeat determinations of the elevation of the snow surface. The limitation in precision is due to short-term fluctuations in snowfall and near-surface densification, whose importance is as yet unknown but is believed to be critical (Reference Wingham, Ridout and ArthernWingham and others, 1997).
There is some disagreement in results. Reference Zwally, Brenner, Major, Bindschadler and MarshZwally and others (1989) and Wingham (1995) used radar altimetry to find that southern Greenland is thickening rapidly. Krabill and others (1995) confirmed this with repeal airborne tracking of the ice-sheet surface. However, Reference Kostecka and WhillansKostecka and Whillans (1988) presented measurements of flow divergence in Greenland that approximately balance snow accumulation and so indicate steady state. The difference may be in the time-scale of significance. The thickening may be a very recent phenomenon.
A new method under development entails measuring time changes in acceleration due to gravity at the edge of the ice sheet (Reference Wahr, Han and TrupinWahr and others, 1995).
Many of these methods suffer from difficulties in obtaining results thai apply to a long enough time-scale such that ordinary fluctuations in precipitation (cf. Van der Veen, 1993) do not dominate the error budget.
Discussion
Ice-sheet thinning and near-balance are found for the two studied sites. They represent a very poor sampling of the ice sheet. Nevertheless, these measured imbalances can be placed into a perspective relevant to global sea-level change. Supposing that all of Antarctica is thinning at the average measured rate, a global sea-level rise of about 0.001 m a−1 is indicated.
These first results have uncertainties of about 0.02-0.04 ma−1. For both sites, the uncertainties derive mainly from the precision oflhe vertical velocities from long-term GPS tracking. These uncertainties can be reduced by increasing the occupation time at the pole, the frequency of occupations and, most especially, the time interval between first and final surveys. Unfortunately the early surveys used short occupation times, now known to be too short for best-quality work.
Merits of the “coffee-can” method include small cost and immunity from decadal and shorter time-scale effects. Field costs are small, being mainly the outcome of the logistics of flying two people to the site to install and, in later years, to remcasurc and service the markers. Because the markers are subsurface, near-surface fluctuations in density or snow accumulation do not affect them.
The major demerit of the technique is that results apply only to the sites visited. By this method, it is not feasible to obta in the average mass balance over an entire catchment area. Thus, the “coffee-can” method is best augmented with satellite and airborne laser or sled-mounted kinematic GPS to extend the results over wider areas, using the “coffee-can” sites as fiducial control on long-term significance, and so obtain regionally significant mass-balance results with long-term significance.
Archive
The GPS tracking data and the solution results are retained in the daily storage system at the University of Canberra (P.J.M.). The field notes and local surveys are archived at The Ohio Stale University (G.S.H.). Contact these people for access.
Acknowledgements
We thank K. van der Veen, J. Zwally and an anonymous referee for helpful comments. The work was supported by the U.S. National Science Foundation (OPP-9419396), BPRC contribution C-1093 and the University of Canberra Research Committee.






