Frictional relaxation in avalanches

Abstract

We use velocity profile measurements captured at the Vallée de la Sionne test site, Switzerland, to find experimental evidence for the value of extreme, Voellmy-type runout parameters for snow avalanche flow. We apply a constitutive relation that adjusts the internal shear stress as a function of the kinetic energy associated with random motion of the snow granules, R. We then show how the Voellmy dry-Coulomb and velocity-squared friction parameters change (relax) as a function of an increase in R. Since the avalanche head is characterized by high random energy levels, friction decreases significantly, leading to rapidly moving and far-reaching avalanches. The relaxed friction parameters are near to values recommended by the Swiss avalanche dynamics guidelines. As the random kinetic energy decreases towards the tail, friction increases, causing avalanches to deposit mass and stop even on steep slopes. Our results suggest that the Voellmy friction model can be effectively applied to predict maximum avalanche velocities and maximum runout distances. However, it cannot be applied to model the full range of avalanche behaviour, especially to find the distribution of mass in the runout zone. We answer a series of questions concerning the role of R in avalanche dynamics.

1. Introduction

A key problem in snow science is to physically explain the low friction values required to model extreme runout of dense flowing avalanches. These low values have been deduced from back-calculation of avalanche events (Buser and Frutiger, 1980), but must be changed from event to event, primarily depending on avalanche size (Salm and others, 1990; Gruber and Bartelt, 2007). Although empirical, they are the basic requirement for the predictive application of avalanche dynamics models in practice.

In this paper, we model avalanche friction by introducing a frictional process based on tracking the kinetic energy R of the random motion of the snow granules (Buser and Bartelt, 2009). We show that this process is capable of modelling the continual evolution of internal avalanche velocity and therefore can predict the heightened mobility of avalanche fronts as well as the stopping behaviour of avalanche tails. In the discussion we answer a series of questions to help explain the role of random kinetic energy in avalanche flow, especially questions regarding the relationship between R and mechanical work, frictional shearing, avalanche velocity and flow density.

2. Random Kinetic Energy

We shall denote in two dimensions

(1)

the kinetic energy associated with the fluctuating velocites u_r (P, t) and w_r (P, t) of snow granules moving within a flowing avalanche with continuum density p at time t at point P (Fig. 1). The motion is defined within a rectangular plane defined by the Cartesian coordinates x and z, P(x, z). The fluctuation velocities are mathematically defined as the difference between the instantaneous avalanche velocities, u(P, t) in the horizontal direction and w(P, t) in the vertical direction, and the steady average velocity, u(P) and w(P) = 0:

(2)

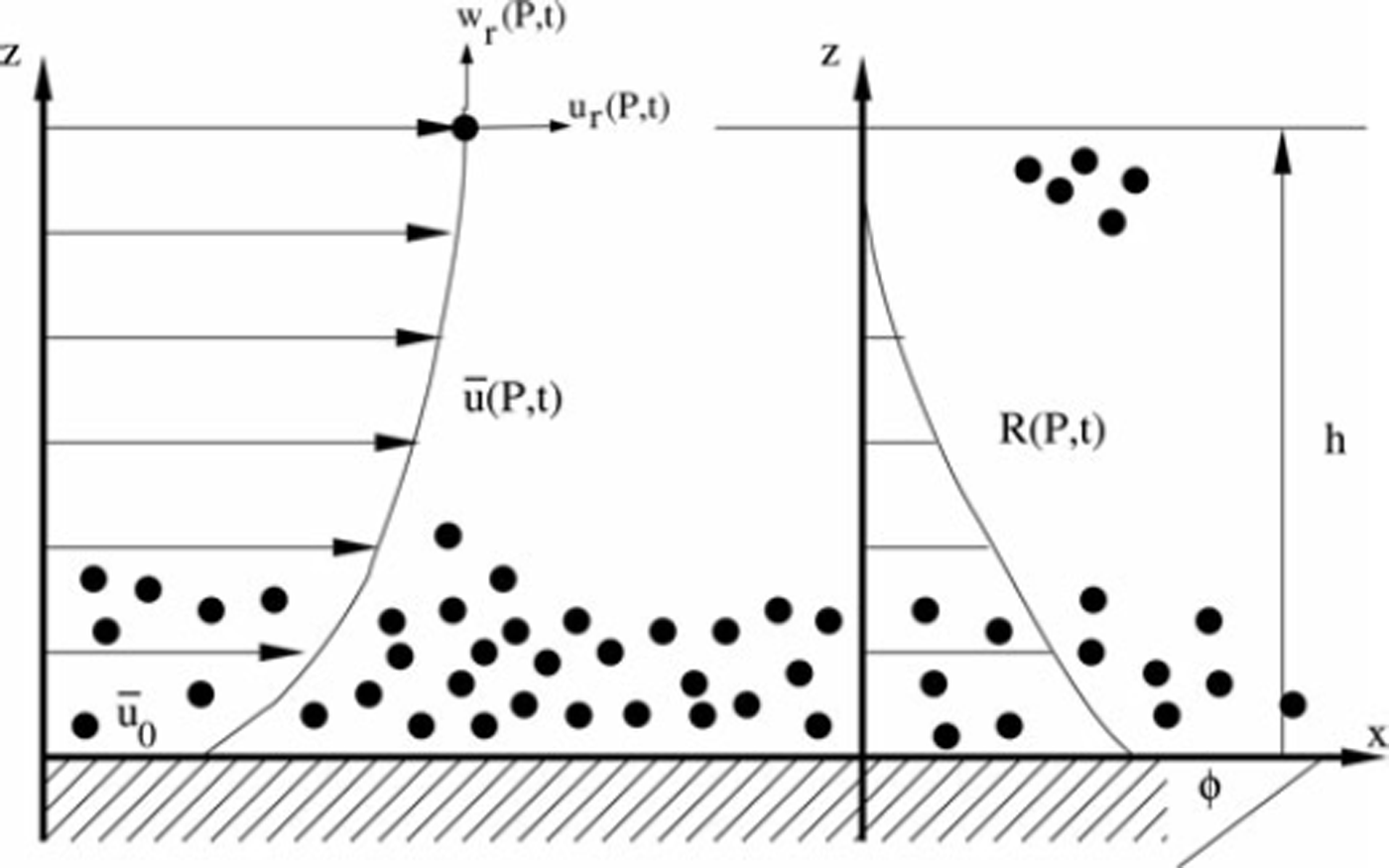
Fig. 1. Avalanche cross-section. Definition of coordinate system, velocity u(P; t) and random kinetic energy distribution R(P; t).

and

(3)

We therefore divide the total flow velocity into two separate flows – the mean flow and the fluctuating flow – although both flows are associated with the same mass. The steady average velocity is also time-dependent, but on a much longer timescale than the fluctuation velocities, which primarily represent any velocity component not in the mean flow direction, which is always defined either parallel or perpendicular to the slope with angle ϕ(x) (Fig. 1). By definition, the fluctuation velocities have zero mean, so they can be considered random. As such, the random kinetic energy R(P, t) cannot perform mechanical work (Bartelt and others, 2006). Energy fluxes associated with the production and dissipation of R(P, t) are therefore irreversible because the density is constant (Buser and Bartelt, 2009).

3. Frictional Relaxation

Experiments with real-scale avalanches (Salm and Gubler, 1985; Gubler and others, 1986; Gubler, 1987; Kern and others, 2009) have led us to apply the constitutive equation for shear stress S_zx,

(4)

to predict the evolution of measured shear rates

(5)

of the mean velocity field in avalanches observed at the Vallée de la Sionne (VdlS) test site, Switzerland (Fig. 2) (Buser and Bartelt, 2009). Because the constitutive Equation (4) contains a dry-Coulomb part (coefficient b) and a viscous part (coefficient m), it can model avalanche flow just after release and near stopping (when the granular avalanche behaves as a solid block) and when the avalanche is moving rapidly in the acceleration zone (when the avalanche moves as a viscous fluid). We now adjust the constant Coulomb friction coefficient b and the effective viscosity m with correcting terms (b′ and m′) to account for different friction values, depending on the velocity, etc. The height of avalanche flow h(t) and density at P defines the normal stress N(P,t) if vertical accelerations are negligible.

Fig. 2. Examples of avalanche velocity profiles from VdlS (see Buser and Bartelt, 2009; Kern and others, 2009): (a) velocity avalanche head; (b) velocity avalanche tail. Velocity profiles are fitted assuming shear stress Equation (4).

The parameters b′ and m′ depend on the random kinetic energy R(P,t) and account for frictional relaxation leading to extreme avalanche runout. These coefficients are determined by two thermodynamic constraints. Firstly, all combinations of b′ and m′ must satisfy the second law of thermodynamics. For each frictional process (Coulomb and viscous), we cannot reduce the friction such that we violate the second law. Secondly, if the avalanche is in steady state, the increase in heat generation must be zero (Bartelt and others, 2006). In this case, an increment in frictional heat must be followed by an equal decrement in the dissipation of R and vice versa. This indicates that the two heat-producing processes must be symmetric. We impose these two constraints on our constitutive formulation by completing the squares of the two heat-producing processes. Letting represent the dissipation by Coulomb friction

(6)

and represent the dissipation by viscous shearing,

(7)

we find

(8)

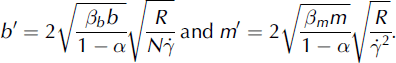
The parameters α and β = β_b + β_m parameterize the production of random kinetic energy by the mean flow field and its dissipation, namely,

(9)

The parameter α ∈ [0,1] describes the generation of random energy from the mean flow, while the parameter β = β_b + β_m (with β_b ≥ 0 and β_m ≥ 0) accounts for the dissipation of random energy. We assume that the generation depends only on the local strain rate and that no energy is transferred from the mean flow field to larger-scale flow structures (vortices) and is associated only with the random velocities of the granules.

To fit the measured velocity profiles, we assume three values: μ = [b – b'], m and β_m /(1 − β). The values b, m, β_b , β_m and a are constant for each avalanche. They do not change as a function of location or time. For each measured velocity profile, we then select R(z) and solve the momentum balance equation in simple shear (Buser and Bartelt, 2009). The calculated velocity profile is then compared to the measurements (Fig. 2). In the previous work, only the viscous friction term was relaxed, but strong variations in μ were noted (Buser and Bartelt, 2009). These variations can be explained by reducing all frictional processes, not only the effective viscosity, in accordance with the thermodynamic constraints outlined above. We find good agreement between the selected μ values and the values predicted by the constitutive model, that is [b – b'] where b′ is defined by Equation (8) (Fig. 3a). Our analysis of the experimental results from five avalanches observed at the VdlS test site (Buser and Bartelt, 2009; Kern and others, 2009) reveals that 0.15 ≤ β _b ≤ 0.25 and 0.55 ≤ β _m ≤ 0.65 (Fig. 3b; 0.75 ≤ β ≤ 0.85). The production parameter a varies between 0.10 ≤ a ≤ 0.25, leading to fluctuation velocities that are 20–30% of the mean translational velocity at the avalanche head but are close to zero at the avalanche tail.

Fig. 3. Relaxation of Coulomb friction. (a) Comparison between μ values found from velocity profiles and Coulomb friction values deduced from [b – b'(R)]; (b) dissipation coefficients βb and βm from VdlS measurements.

4. Voellmy Parameters

The Voellmy friction equation (Buser and Frutiger, 1980; Bartelt and others, 1999) has long been applied in avalanche science to predict avalanche runout:

(10)

The two Voellmy coefficients are the dry friction coefficient μ and the turbulent friction coefficient ξ (ms⁻²). For agreement with other applications of the Voellmy model, we define the coefficient s = ρg/ξ (Norem and others, 1987). The model relates mean avalanche velocity U_m(x, t),

(11)

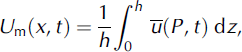
to the total shear stress. Shear gradients are therefore concentrated in a thin layer at the avalanche bottom (Salm, 1993). From the experimental data we can find both the mean flow velocity (Equation (8)) and the mean random kinetic energy R_m(x, t),

(12)

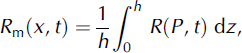
and therefore find the dependency of μ and ξ on the mean values U_m and R_m. Moreover, we define

(13)

and

(14)

The results from five avalanches observed at the VdlS test site are depicted in Figure 4. We find that μ(R _m) decreases to μ(Rm) =0.15 for high mean random kinetic energy levels at the head of the avalanche (Fig. 4a). Similarly, the turbulent friction ξ(R _m) increases to ξ = 2000 ms⁻² (Fig. 4b). These μ and ξ values are similar to the recommended guideline values (Buser and Frutiger, 1980; Salm and others, 1990) as well as Coulomb friction values found in snow-chute experiments (Platzer and others, 2007). Figure 4c depicts the results for the variable s(R _m). Note that s(R _m)decreases to values s(R _m) = 0.5 kg m⁻³, in good agreement with Norem and others (1987) or Bartelt and others (1999). At the tail, friction values increase, indicating that an avalanche can stop on steep slopes if the mean random kinetic energy decreases to small values such that μ(R_m ) ≈ tan(/> (Bartelt and others, 2007).

Fig. 4. Voellmy friction parameters as a function of the mean random kinetic energy: (a) Coulomb friction μ(R_m); (b) turbulent friction ξ(R _m); and (c) s(R_m). The values relate to values near Swiss guideline recommendations (Salm and others, 1990; Bartelt and others, 1999).

The change in parameters μ(R _m) and ξ(R _m) can be expressed in differential form as

(15)

with μ(R _m = 0) = μ ₀ and ξ(R_m = 0) = ξ₀. Typical values for snow avalanches are 0.30 ≤ μ ₀ ≤ 0.4, 50 m s–₂ ≤ ξ₀ ≤ 300 m s–₂; R ₀ ≈ 6kJ m–₃. This relation indicates that the change in shear stress is a function of the shear itself, reflecting the fact that the shear rates 7 are a function of R(P, t) (Equation (4)), while conversely R(P, t) is a function of the shear rate 7 (Equation (9)).

5. Discussion

The following questions are raised so often that we decided they deserve a special section.

Why do the authors ignore the role of the dispersive pressure, pd, which is due to the random kinetic energy R?

Because our experimental measurements indicate that in the mean the dispersive pressure is zero. When we measure the normal pressure at the bottom of the avalanche, either in snow-chute experiments (Platzer and others, 2007) or granular experiments (Bartelt and others, 2007), we find that the normal pressure acting on our force plate is equal to the weight of the avalanche. This experimental result implies that the acceleration of the centre of mass is zero in the vertical direction (normal to the slope); otherwise we would see a change in pressure as the centre of mass is accelerated upwards or downwards by the dispersive pressure. This experimental result is the first indication that R, in a flowing avalanche, does no mechanical work. If R did mechanical work, we would see some deviation from the self-weight pressure at the bottom of the avalanche.

How can R do no mechanical work? When random energy exists inside a closed container it exerts a pressure on the side walls and can increase the volume of the container, like a gas in a combustion engine

For R to do mechanical work we would have to have a corresponding change in either the position (potential energy) or velocity (kinetic energy) of the centre-of-mass of the flow volume we are considering. In the container problem, R accelerates the piston and we see the transfer of internal energy to kinetic energy as well as a rise in the centre of mass. If we were to measure the weight of the container, we would measure the self-weight plus the acceleration force of the piston as it is pushed upwards. If the piston did not move, we would simply measure the weight of the container. What we measure in our experiments is more similar to the piston which is not moving than the system where the piston is being accelerated upwards. We simply do not observe large deviations from the self-weight of the flow material as it moves across the force plate.

But if the internal pressure or R increases and the piston did not move, or moves with contact velocity, what happens?

If the piston is not pushed or accelerated upwards, we cannot measure any change in weight or normal force, although the dispersive pressure or R increases. Moreover, nothing happens. This has two important consequences. Firstly, the sum of the velocity fluctuations must be zero; that is, the centre of mass does not move. Secondly, the sum of the fluctuation velocity squared has certainly increased, raising the internal pressure. But because the centre of mass does not move upwards, this rise must be compensated by an equal rise in internal friction in the flow plug. Again, R cannot do any mechanical work. In our avalanche model, we enforce this result by defining the velocity fluctuations with respect to the steady-on-average velocities of the volume. This averaging procedure, which is often invoked in turbulence theory, ensures that R in fact does no mechanical work when we have no vertical accelerations.

If R does no mechanical work, why consider it?

Because we are interested in frictional shearing. Consider a block sliding down an incline that is lubricated with a thin oil film. The properties of the film are a function of its thermal temperature (or the temperature dependence of the viscosity, or a function of the random movement of the oil molecules, or the random kinetic energy, or the dispersive pressure – whichever reason the reader prefers). The oil film itself does no mechanical work. However, the film influences the position and speed of the block or block’s centre of mass. Now the speed of the block influences the generation of heat in the oil film. There are also heat losses. The final velocity will be reached when there is no temperature change within the oil film, i.e. when we have equilibrium between the generation and losses of heat. This familiar picture of lubrication can be applied one-to-one to the avalanche problem, replacing the generation of heat with the production of R and the loss of heat with the decay of R.

What is the relation between frictional shearing and R?

Our understanding of the interaction between R and frictional shearing began with simple chute experiments. We measured the shear S and normal forces N at the bottom of granular avalanches and saw firstly that the normal force corresponds to the height of the avalanche, i.e. no dispersive pressure. Secondly, we observed that the shear force at the front of the avalanche is different from the shear force at the tail, although the flow height and the velocity could be the same. When we plotted S/N vs N we found a straight line for N ≠ 0, but S/N=0 for N=0. This result suggests that the tangent modulus dS/dN is more or less a constant, but S/N, the secant modulus, is far from a constant (Bartelt and others, 2007). On closer examination we discovered a hysteresis, showing that dS/dN can change between the front and tail of the avalanche. The interpretation of the experimental results was more difficult than we imagined, because at every slope angle the dS/dN was different, although the running surface and material did not change. Sometimes we found that dS/dN was near to the tangent of the slope angle, implying some near-steady flow behaviour, but never for the entire flow. The velocities differed, but only slightly, and could not be explained by some simple velocity-dependent rheology. The sum of this behaviour led us to believe that we have some memory effect due to the time-dependent and competing processes of the production and decay of R.

One implication of the paper is that the U_m ² drag term of the Voellmy model can be derived directly from the R model. Furthermore, it appears that m′ is independent of the shear rate. What is the relationship between flow velocity and friction?

We performed chute experiments with snow and granular materials at different slope angles, hoping to find some simple U _m ² drag term. Of course, we found that the steeper the slope angle, the faster the flow. However, we could not find a drag law relating mean velocity U _m or the mean velocity squared U _m ² to the measured shear stress S. For each slope angle and for different locations in the avalanche we found different drag coefficients. Sometimes we found no velocity effect at all (Platzer and others, 2007). This result reinforced our idea that we have some memory effect, and a constitutive relation based on a nearly instantaneous balance between creation and dissipation of random energy could not describe our observations. In an avalanche the velocity depends on the shear stress, and the shear stress depends on the velocity. The velocity and shear stress are continually readjusting, especially when the avalanche encounters slope angle deviations. The velocity and shear stress can reach equilibrium, but the equilibrium will vary from one slope angle to the next. For the entire avalanche, it is impossible to express this complex process with a simple U _m ² drag term. We rewrite our results in terms of Voellmy parameters only because this is the most often applied model in avalanche dynamics.

What does R ‘compete’ against?

All the kinetic energy we place in the random motion of the granules must eventually be dissipated, i.e. transformed to internal heat energy. Therefore we must treat R as an irreversible energy flux (that as such does no mechanical work). R therefore has a distinct one-way character. However, where does R come from? It comes from the frictional shearing. If we produce some R from this frictional work rate, we must reduce the amount of heat produced by exactly the amount we need for producing R. Otherwise we have a mismatch between heat generation and frictional work. Therefore, R and the direct production of heat compete against each other. In our model, this competition is defined by the parameter α.

What is the importance of this competition?

The competition determines the reduction in friction. We repeat, when we produce some R, then we must reduce the heat produced by a corresponding amount, since both processes share the irreversible work done by shearing. This means reducing the friction, since the frictional work and the heat generation are the same thing. This process ensures that the source of all movement, the gravitational work rate, is divided up correctly, i.e. that it conserves the potential energy and that our direct heat-producing processes are associated with the frictional work. In Buser and Bartelt (2009) we presented a flow chart of the energy fluxes. In reality, this flow chart is a construct since everything happens at the same time: potential energy is transformed simultaneously into kinetic energy, random energy and heat. In a short time interval, we need some simple bookkeeping to track the energy fluxes because at the same time random energy is being produced, the heat generated is decreasing.

Why all this thermodynamics? Why not apply force mechanics to determine the appropriate constitutive model?

The avalanche problem must be solved with force mechanics and momentum balances. A constitutive model reflects the relationship between shearing and deformation and therefore is a force balance. We will always need to solve these equations to predict avalanche runout. However, thermodynamics was essential for the development of statistical mechanics since no microstructural and complicated deterministic model of atomic interactions was necessary. The avalanche problem is similar. Although we cannot attribute the reduction of friction to some mechanical process at the microstructural level (at least not for now), we can predict what the overall consequences will be when random kinetic energy is produced in an avalanche. This opens the door to both useful and simple avalanche dynamics models as well as bringing a step nearer the solution of the microstructural problem.

What is the relation between flow density and R?

It would be natural to assume that the higher R, the lower the density. However, we do not think the relationship is so simple. For example, to create R one needs a certain density; one needs mass to have granular interactions and therefore produce R. We could imagine the upper regions of the avalanche have low density, but all the particles move with the same (mean) velocity, so we have low density but no R. Furthermore, if we have little mass, R no longer remains random because there are too few interactions to maintain the randomness. For example, if particles reach the top of the flow, R is no longer random. In this case the particles fly away or increase the flow height. The piston and the centre of mass move upward, so we are doing true mechanical work. We simply do not let this happen, by keeping the density constant, which agrees with the stipulation that R can do no mechanical work.

Why not consider a density change when considering avalanche flow? Observations would certainly support the idea that the density is not constant

Small and local changes in density at the base of the avalanche appear to have a large influence on the frictional behavior. We account for these changes with R, not by tracking the local variations in density directly which would be computationally difficult. However, it likewise appears that large bulk changes in density are not as important as we imagine. To understand why, we must ask the question, ‘how does a bulk density change affect the movement of a dense flowing avalanche?’ In order to decrease the density, we must increase the height of the avalanche and keep the mass constant. This increase in height can be accomplished in one of two ways: steadily, with a constant upward velocity, or suddenly, by accelerating the mass upwards. A steady increase in height does not affect the normal pressure. Only when the rate of change of the height increases, i.e. when the mass is accelerated, will we see an effect on the normal pressure measurements. If we let z _m represent the z location of the centre of mass, then the vertical acceleration is The additional normal pressure at the base of the avalanche is then . If the normal pressure remains unchanged, we expect little change in the frictional behaviour although the height is increasing. Since the production of R is a function of the total mass (not the mass density), the bulk density change will not affect R. In most cases, the additional acceleration due to h is small in comparison to gravity. This helps explain why depth-averaged models, which make this assumption, can simulate dense flowing avalanches. However, we believe that we can see these second-order effects in some of our measurements. This is the problem we are now working on.

Therefore, should we not consider density changes?

To predict avalanche impact pressures and flow heights, engineers will need to assess the flow density. The influence of density changes on the frictional behaviour of avalanches will require a model that accounts for vertical accelerations.

Can an avalanche reach a steady flow state?

Avalanches are ‘finite-sized’ mass movements and will hardly reach a steady flow state. Because the mass in the upper flow regions travels faster than at the bottom, where the basal friction is greatest, this finite mass elongates. A tail develops which can eventually stop, depending on the slope angle. If the tail stops, mass ceases to travel to the front and the avalanche starves. The front can then stop if the slope angle is not too large. This process, which can be observed every winter when small avalanches release and stop on slopes with more or less constant inclination, underscores the fact that the mass is finite, so it is impossible for an avalanche to reach a true steady state. Of course, if the avalanche entrains material and can maintain the front, a steady flow state can be achieved. In this case, there is a region between the front and tail where the mass travelling to the front is equal to the mass lagging behind. The mass lost to the tail might be compensated. If there is no entrainment, this region can exist, but only briefly, and will disappear as the avalanche travels downslope and starves. This region can be observed in experiments with force plates if one chooses the right slope angle for the given granular material. If the slope is too steep, the front accelerates as it passes the force plates; if the slope is too shallow, the flow decelerates. If one selects the right slope angle, it is possible to see all the conditions of steady state fulfilled: constant flow height, constant velocity and tan φ = S/N but only for this region in the middle. However, what is measured depends strongly on where the force plate is positioned. If the force plate is positioned, say, 1 m downstream, it could be that the steady middle region has disappeared since the flow form of the avalanche evolves continuously. The tail of the avalanche is truly fascinating, since as the mass slows down, one will often measure tan φj) = S/N, which must exist as the avalanche stops. Turnbull and McElwaine (2007) have reported that powder-snow avalanche fronts travel with constant velocity, which we believe is correct, but how long that velocity is maintained depends on how long the avalanche can supply the front with mass to compensate the tail losses.

If this is the case, why do you consider steady states to find your flow parameters and fit the velocity profiles?

One way to answer this question would be to cite Kolmogorov’s famous turbulence paper (Kolmogorov, 1991): ‘Within small time intervals it is natural to consider this regime steady, even in the case when the flow on the whole is not steady.’ Therefore, any steady state is defined by the time interval of observation. The velocity profiles are found by optical sensors using a correlation procedure (Kern and others, 2009). If the accelerations are large, it is simply not possible to correlate any signals. Thus, the fact that we can correlate our measurements implies that for this small time interval (the time interval of the correlation), the flow is steady for our time interval of observation. Another argument would be the following: we first find the model parameters by fitting them to the velocity profiles assuming steady flow. We then use the parameters we have found to numerically model the entire flow, dropping the assumption of steady state. We find we can model the highly non-steady behaviour of the whole avalanche, such as the stopping of the tail or the mobility of the front. In this case, the assumption of steady flow can be validated when the model parameters satisfactorily reproduce the entire avalanche behaviour. This result would justify our assumption of steady state for the velocity profiles.

Why does the tail stop?

The tail is the tail because it is the tail - meaning that the tail is the tail because it has a small flow height and low velocity. No mass is available from behind the tail, because the mass is finite. Small flow heights and velocity translate into small gravitational work rates. Remember that the gravitational work rate is the source of all energy in an avalanche: kinetic, internal (heat) or random. Because the gravitational work rates decrease at the tail, the production of R also decreases, causing the friction to increase. As R decreases, other microeffects could come into play (e.g. sintering and microroughness), but we first prefer an explanation based on energy fluxes, before invoking micro-properties, which might or might not play a role. One of the salient features of all gravitational mass movements, especially snow avalanches, is the size effect: large events travel farther than small events. This size effect can be simply explained as the competition of R with the other energies to get the most gravitational work. Often one sees considerable basal slip at the tail because the flow locks up (no R) and then slides as a rigid block. Before modelling this process, we think it is important to model the plug or the lock-up behaviour first.

The frictional parameters in the R model are not microstructural parameters, but rather continuum parameters, viscosity and Coulomb friction. But surely the interactions between the granules would be better described by microstructural parameters?

Of course, a microstructural model would better describe the processes we are interested in. However, at the moment we can only measure bulk properties of the avalanche flow (e.g. shear and normal forces or flow velocities). To determine the parameters required to develop a microstructural model, valid for snow avalanches, we would require the particle size and shape distributions, particle agglomeration, disintegration or abrasive wear characteristics, to name but a few. We try to lump all of these processes in a production and decay coefficient. Our hope is that the production and decay coefficients reflect the statistical mean of all these microscopic properties.

The model now has five parameters (a, β, R0, (μ0, ξ0). You state that the Voellmy model can be used, but then why replace a two-parameter model with a five-parameter model?

It is too early to speak about replacing the Voellmy model which is the backbone of the Swiss guideline procedure for runout calculations. But it is very comforting to know that a more physics-based model can explain the Voellmy parameters (e.g. why the Voellmy parameters change) or the avalanche behaviour that the Voellmy model cannot explain (e.g. the starving and deposition process, why small avalanches stop on a steep slopes, and the mobility of large avalanches). This is helpful, especially when dealing with dam design, where the volume and distribution of mass along the avalanche length is of importance. When we back-calculate avalanches, we now take γ ₀ to be the angle of repose of avalanche deposits; we determine ξ ₀ from the velocity of the tail; velocity profile measurements in VdlS reveal that β=(1 – α) varies between 0.8 (dry avalanches) and 1.2 (wet avalanches). We do not say the Voellmy model is now useless, merely that our theory can explain a wider range of avalanche behaviour. In the limit of large avalanches, the R model reduces to the Voellmy model. In a way, we have developed an even stronger respect for Voellmy and Salm. They achieved a considerable success with fewer resources, and never aimed at modelling the full range of avalanche behaviour, as we do not aim at modelling all the microstructural interactions.

6. Conclusions

Voellmy-type models containing a combination of Coulomb and turbulent friction have long been applied to the avalanche problem, with little or no experimental verification. Although the Swiss guidelines for extreme runout calculation recommend values of μ = 0.155 and ξ≈2000m s⁻², these values were based on back-calculations of observed extreme avalanche events (Buser and Frutiger, 1980), not on direct and independent measurements. Using actual measurements from the VdlS test site, we find that these μ and ξ values correspond to high R levels encountered in the observed VdlS avalanches. Since it is the head of the avalanche which governs the maximum flow velocity and runout distance, there appears to be some experimental validity to the guideline values. However, the Voellmy model will not predict the distribution of mass in the runout zone, which appears to be governed by high μ and low ξ friction values (low R levels), causing the avalanche to stop, even on steep slopes. Since the production of R depends on the gravitational work rate (which finally produces the shear deformations in the avalanche body) and therefore on the mass, larger avalanches will experience a corresponding larger decrease in friction. Thus, size effects are an intrinsic part of frictional relaxation in avalanches.