Introduction
Conventional treatments of glacial erosion characteristically discuss four primary mechanisms: abrasion, quarrying, subglacial fluvial erosion, and dissolution (e.g. Reference DrewryDrewry, 1986). In comparison with abrasion and dissolution, which are relatively well defined and have been the subject of considerable analysis (e.g. Reference HalletHallet, 1979; Reference LliboutryLliboutry, 1994; Reference Sharp, Brown, Tranter, Willis and HubbardSharp and others, 1995), little is known about the other mechanisms.
The importance of quarrying (also termed plucking) relative to abrasion is essentially unknown (Reference DrewryDrewry, 1986), and even its existence has been questioned recently (Reference LliboutryLliboutry, 1994). The quarrying phenomenon remains elusive not only in modelers, but even to those attempting to define precisely the controlling processes: subglacial rock fracture, loosening of rock fragments and evacuation of those rock fragments. Nevertheless, quarrying has long been recognized as an important erosional mechanism based on diverse geologic evidence, including: (1) rock fragments on glaciers and erratics in deglaciated areas that had to be derived from the bed; (2) widespread evidence for subglacial rock fracture on proglacial bedrock exposures; and (3) occurrence of quarried lee surfaces on boulders that are embedded in lodgement tills (Reference SharpSharp, 1982), as well as on bedrock hills and roches moutonnées (e.g. Reference JahnsJahns, 1943).
Quarrying also warrants scientific attention because it can play a crucial role in the generation and maintenance of bed roughness, which in principle can profoundly affect the sliding sliced and stability of temperate glaciers (e.g. Reference IkenIken, 1981). Unlike abrasion, which tends to smooth the bed because it is more effective near the tops of bed protuberances than in depressions, quarrying can roughen the bed, thereby permitting the bed micro-relief to persist in spite of extensive erosion. For instance, considerable bed roughness is evident on recently deglaciated bedrock in deeply incised valleys and cirques where erosion can amount to hundreds of meters of surface lowering.
Current consideration of abrasion mechanics by the author directs attention toward quarrying as a key process from yet another point of view: as a sustained source of abrasive material active over large parts of the bed, which is necessary for significant abrasion. Quarrying also affects the accumulation of subglacial sediments, which can influence sliding over bedrock (e.g. Reference ShoemakerShoemaker, 1986), and ultimately leads to soft bed conditions. The widespread realization that sediments, which can deform or facilitate sliding at the base of ice masses, may play a critical role in the dynamics of glaciers and ice sheets (e.g. Reference Alley, Blakenship, Bentley and RooneyAlley and others, 1986, Reference Alley, Blankenship, Bentley and Rooney1987b; Reference BoultonBoulton, 1987), and in their response to global change (Reference Alley, Blankenship, Bentley and RooneyAlley and others, 1987a), provides ample motivation to study quarrying as a primary source of subglacial sediments. Consideration of sources and sinks of rock debris at the base of glaciers is fundamental to understanding why debris accumulates and lubricates the bed in certain areas and not in others.
Previous Models
Several analyses have addressed quarrying in the context of current glaciological understanding. Rothlisberger and Reference IkenIken (1981) proposed that local basal freezing enables a glacier to extract rock fragments from the sufficiently jointed bed. Such freezing could result from the rapid opening of large-scale water-filled cavities under high water pressure, or from the heat-pump effect proposed by Reference RobinRobin (1976). Except near the margins of temperate glaciers, where winter temperatures can drop well below the pressure-melting point (Reference Anderson, Hallet, Walder and AubreyAnderson and others, 1982), it is unlikely that ice growth could wedge open cracks in the bed (e.g. Reference Walder and HalletWalder and Hallet, 1985), because the well-buffered thermal regime prevents the build-up of pressure much above the ambient basal ice pressure. Ice growth could create higher pressures in bedrock cracks if temperatures were relatively low there. However, this is precluded because if cracks were relatively cold, heat would naturally converge on the cracks, thereby melting rather than growing ice there.
Hinter and Olunloyo (1981) presented a model for the generation of high basal stress concentrations at the periphery of “cold patches” where ice is frozen to the bed. This mechanism could lead to fracture and entrainment, but only where huge pre-existing flaws render the bedrock weaker than ice. This limitation, which stems from the similarity of the stress field in the rock to that in the ice, also applies to Reference Morland and BoultonMorland und Boulton’s (1975) analysis of quarrying.
Considerable insight into the physics of quarrying was gained by Iversou (1991) who used coupled finite-element models to analyze stresses both in the ice and in the rock. He computed ice loads on a single bedrock ledge, considered important effects of transient pore-pressure gradients in the bedrock, and presented detailed numerical results describing the stress field and an index of the propensity to crack growth under both steady and non-steady conditions. His results provide a very instructive quantitative view of the basal conditions, particularly the water-pressure variations, that are most favorable for micro-crack growth, as well as the location and direction of crack growth. In contrast with previous models, the stresses at the bedrock surface computed by Reference IversonIverson (1991) are not identical to those in the glacier sole. This difference, which arises from ice/bed separation, is important because it circumvents a persistent problem fundamental to quarrying: as rocks are generally more resistant to fracture than ice, how can ice-induced loads fracture the rock without first fracturing the ice?
The model I develop here has much in common with that of Reference IversonIverson (1991), in that both are centered on the state of stress induced in bedrock ledges by sliding ice. I focus on a simple analytical estimate of stresses averaged over those parts of the bed in contact with ice. These spatially averaged stresses are of interest both because they can be easily calculated and because the extreme stresses that lend to dictate crack growth scale directly with average stresses. Streamlining the stress analysis greatly facilitates examination of the role of glaciological parameters in quarrying. It enables me to proceed beyond calculating stress indices, and to evaluate the rate at which microcracks can grow, which is linked to the rate of quarrying. Also, I can consider a series of Sedges, instead of a single ledge cavity pair, which permits definition of critical quantities averaged over the bed, such as the degree of ice/bed separation and an index of the rate of quarrying resulting from progressive sub-critical crack growth in bedrock.
I wish to emphasize that Reference IversonIverson’s (1991) model and the one presented here are complementary in several ways. Whereas Iverson’s model can improve my local stress descriptions, particularly under non-steady conditions, my model delineates how his analysis can be extended to obtain an index of quarrying rates over large parts of the bed. In addition, the factors identified in the respective models as being key to fracturing rock subglacially can operate synergistically, as mentioned in the discussion below.
Present Modeling Strategy
In view of the complexity of the quarrying process, the simplest model is sought that permits analysis of the controlling physics with the conviction that the insight gained from a judiciously streamlined model far outweighs that lost through the required idealizations.
I examine steady sliding over a simple glacier bed comprising periodic ledges stepping down in the ice-flow direction, similar to that used by Reference IkenIken (1981) to study the effect of subglacial water pressure on sliding velocities. Aside from resembling some actual glacier beds (e.g. Reference Anderson, Hallet, Walder and AubreyAnderson and others, 1982), this bed idealization has the following advantages: (1) ice-induced deviatoric stresses can reach the elevated levels required to fracture rock, which are considerably higher than those obtained for low-roughness beds (Nyc, 1969; Reference Morland and BoultonMorland and Boulton, 1975); (2) in the long term, quarrying can cause ledge risers to retreat up-glacier at the same average rate, thereby sustaining the bed roughness while quarrying is active; and (3) considerable insight into glacial sliding and basal hydrology has already been gained from this bed model (Reference IkenIken, 1981; Reference HumphreyHumphrey, 1987; Reference KambKamb, 1987), but it has yet to be utilized to study glacial erosion.
I assume that crack propagation is the rate-limiting factor in glacial quarrying. The other primary process necessary for quarrying, entrainment of fractured rock fragments, evidently occurs more rapidly, otherwise such rock fragments would be abundant in proglacial bedrock areas, which is generally not the case. Hence, I do not consider entrainment further, and estimate the rate of quarrying by evaluating growth rates of bedrock cracks and the amount of material likely to be entrained from the bed once a fracture has propagated sufficiently to free a block from the bed. While generally insufficient to cause rapid (unstable) fracture of bedrock, ice-induced stresses, as will be shown, are likely to be sufficiently high to cause slow propagation of pre-existing micro-flaws in most rocks. The rate of such propagation, known as sub-critical crack growth, can be estimated for a given stress state using existing empirical fracture-mechanical data for rocks (e.g. Reference AtkinsonAtkinson, 1987).
The state of stress in bedrock is obtained by considering the balance of forces at the ice/rock interface and the factors determining the extent of cavities. Once the ice/bed contact stress is evaluated, the state of stress in the rock can be calculated using standard linear elasticity. Herein, I analyze erack growth under steady stresses, and briefly consider the effects of non-steady conditions on quarrying. The analysis of pore-pressure effects, particularly those arising from transient gradients in pore pressure (e.g, Reference IversonIverson, 1991), is beyond the scope of this paper.
The Model
The general trend of the bed is horizontal, and it comprises a series of ledges dipping slightly up-glacier at a small angle β (Fig. 1). Cavities occur down-glacier of each ledge where the ice separates from the rough bed. The convenient choice of a straight roof for the cavity is a reasonable approximation, provided it is unaffected by melting due to flowing water or air (Reference FowlerFowler, 1986; Reference KambKamb, 1987; Reference IversonIverson, 1991). Although considerable melting by running water occurs under temperate glaciers, its overall effect on the shape of cavities scattered over the entire bed can probably be ignored because substantial heat dissipation is highly localized along a few channels where water flows vigorously.

Fig. 1. (a) Geometry of idealized bed for the quarrying model. (b) Stresses and location of probable fracture initiation near the corner of a ledge. Quarrying takes place when fractures propagate downward from the ice-loaded surface and coalesce with the planar discontinuities that define that ledge system, at which point a bedrock block is liberated and the ledge is propagated up-glacier.
The normal stress imparted by ice on the bed is central to evaluating crack growth in the bed. The average of this stress over the area of direct ice/rock contact, σn , is a key unknown, since it is a particularly useful single measure of the magnitude of ice-loading. To evaluate σn , the area of ice/bed contact is assumed to be smooth, so that it supports normal stresses but no shear stresses, in accord with standard glaciological theory (e.g. Reference NyeNye, 1969). Relevant basal stresses averaged over the entire glacier bed include the ice-overburden pressure P i, water pressure P w, basal shear stress λ, and effective pressure, P e = P i – P w. Balancing forces in the horizontal and vertical directions and dividing by the ledge length L measured in the ice-flow direction (Fig. 1a) yield:
Here, S = S/L is the normalized extent of ice/bed separation, and α is the slope of the cavity roof, which can be defined in terms of cavity size:

Combining Equations (1) and (2) leads to an overall equilibrium condition at the glacier bed:
which is equivalent to Reference IkenIken’s (1981).
σ n scales inversely with the extent of subglacial cavities determined by the combination of basal sliding and cavity closure. The rate of closure is itself a function of Pe . The inclination of the cavity roof is taken to parallel the ice-velocity vector obtained by the vector addition of the sliding velocity, U, and closure velocity, C, assumed normal to the cavity roof:

The closure of a cavity that is elongated normal to the ice-flow direction, as shown in Figure 1, is similar to the contraction of a cylindrical hole in a glacier, a problem analyzed by Reference NyeNye (1953). The highly non-uniform stress field in the vicinity of a rough bed is likely to render the problems quantitatively distinct. However, it is reasonable to make the conventional assumption that closure rates for both situations have the same form (Reference WalderWalder, 1986: Reference HumphreyHumphrey, 1987; Reference KambKamb, 1987), yielding:
where k is a constant and l is the length of the cavity roof measured in the ice-flow direction. Substituting Equation (6) into Equation (5) leads to

where δ is the elevation difference between the points of separation and contact between the ice and the bed (δ ~ S tan α). A quadratic expression for S is obtained by substituting Equation (3) into Equation (7):
Knowing the cavity extent S, a particularly instructive relation can be obtained for σn using Equation (2):

As expected, the presence of cavities elevates the ice/rock stress above the ice-overburden pressure, and the effect is extreme where ice/bed separation is nearly complete (as (l-S′) → 0).
From the standpoint of rock fracture and quarrying, it is the difference between the normal stress on the ledge and that exerted on other parts of the bed by water in cavities that gives rise to deviatoric stresses in the rock. Based on Equation (2), this difference is simply

In this simple model, cavity size is primarily dictated by effective pressure and sliding velocity, and secondarily by the size and inclination of bedrock steps. At low P e, cavities are extensive, and very large compressive normal stresses are concentrated on ledge corners. However, σn cannot exceed the stress that can be mechanically sustained by ice.
The state of stress in the ice near the corner of a bedrock ledge resembles that due to a localized surface load pressing against and moving along the ice. A conservative indication of the maximum attainable contact stress, ![]() , can be obtained from the simple Hertzian problem (e.g. Reference Frank and LawnFrank and Lawn, 1967) for a sphere pressed against an elastic half-space with average pressure σn
. Brittle failure is expected in the ice if σn
leads to tensile stresses comparable to the tensile strength of ice, which is on the order of 1 M Pa (Reference Palmer., Goodman, Ashby, Evans, Hutchinson and Ponter.Palmer and others, 1983; Reference Schulson, Lim and LeeSchulson and others, 1984). For this problem, the maximum tensile stress is approximately σn
/6, hence
, can be obtained from the simple Hertzian problem (e.g. Reference Frank and LawnFrank and Lawn, 1967) for a sphere pressed against an elastic half-space with average pressure σn
. Brittle failure is expected in the ice if σn
leads to tensile stresses comparable to the tensile strength of ice, which is on the order of 1 M Pa (Reference Palmer., Goodman, Ashby, Evans, Hutchinson and Ponter.Palmer and others, 1983; Reference Schulson, Lim and LeeSchulson and others, 1984). For this problem, the maximum tensile stress is approximately σn
/6, hence ![]() . No experimental data for temperate ice exist to validate this
. No experimental data for temperate ice exist to validate this ![]() estimate. However, it is consistent with recent theoretical and experimental work (Reference Premachandran and HoriiPremachandran and Horii, 1994, p. 33) that reports indentation strength, equivalent to
estimate. However, it is consistent with recent theoretical and experimental work (Reference Premachandran and HoriiPremachandran and Horii, 1994, p. 33) that reports indentation strength, equivalent to ![]() , of around 5 MPa for ice at −10°C for the lowest strain rates considered (2.3 × 10−5 s−1); strength increases with strain rate, which in this context, is defined as indentation rate divided by indentor width. The cited rate corresponds roughly with ice converging with a 0.1 m portion of the bed at 100 m a−1.
, of around 5 MPa for ice at −10°C for the lowest strain rates considered (2.3 × 10−5 s−1); strength increases with strain rate, which in this context, is defined as indentation rate divided by indentor width. The cited rate corresponds roughly with ice converging with a 0.1 m portion of the bed at 100 m a−1.
The above estimate of maximum contact stress ( ![]() ) in the ice, based on a circular contact area, is conservative, however. More realistically, the ice/bed contact area near a ledge corner would be narrow in the direction of sliding and long transverse to it. For this contact geometry, the analysis of a concentrated line load on an elastic half-space (Reference Timoshenko. and GoodierTimoshenko and Goodier, 1951) is also relevant. It suggests that for the strictly two-dimensional model, higher
) in the ice, based on a circular contact area, is conservative, however. More realistically, the ice/bed contact area near a ledge corner would be narrow in the direction of sliding and long transverse to it. For this contact geometry, the analysis of a concentrated line load on an elastic half-space (Reference Timoshenko. and GoodierTimoshenko and Goodier, 1951) is also relevant. It suggests that for the strictly two-dimensional model, higher ![]() can be sustained locally because stresses in the ice are all compressive. Thus, for actual ledges with finite extent in the direction transverse to ice flow, the highest attainable
can be sustained locally because stresses in the ice are all compressive. Thus, for actual ledges with finite extent in the direction transverse to ice flow, the highest attainable ![]() value is likely to exceed the above 6 MPa estimate. Also, account must be taken of the supporting role of water surrounding the ice/bed contact area. Therefore, it appears appropriate to constrain
value is likely to exceed the above 6 MPa estimate. Also, account must be taken of the supporting role of water surrounding the ice/bed contact area. Therefore, it appears appropriate to constrain ![]() not to exceed ~ 10 M Pa, because of the finite strength of ice.
not to exceed ~ 10 M Pa, because of the finite strength of ice.
Once the contact stress is estimated, the stress slate in the bed can be calculated, making the widely accepted assumption that rock can be adequately modeled as a linear elastic material. Focusing on the area near a ledge corner where ice loads are most concentrated, the stresses in the rock must he close to those in an infinite elastic quarter-plane due to a normal stress applied near the corner. According to Reference HetényiHetényi’s (1960) analysis of the quarter-plane problem, tensile stresses could reach magnitudes of ~2(σ n – P w)/3 close to the corner but directly up-glacier of the ice contact zone. This amounts to about 6 M Pa (with (σ n – P w) ~ 10 M Pa), which approaches the tensile strengths of tough crystalline rocks without macroscopic flaws, which generally range from 10 to 20 M Pa. A considerably lower tensile stress would suffice to fracture any rock with sizable pre-existing cracks.
The state of stress in the rock can be related to its fracture behavior by introducing the stress intensity factor, K 1 which provides a measure of the stress concentration at critical areas, the tips of pre-existing cracks. Here I consider only the opening mode for idealized penny-shaped cracks of radius c oriented perpendicular to the direction of maximum tensile stress below the rock surface. For this situation
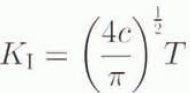
where T is the far-field tensile stress (T ~ 2(σ n – P w/3). Above a critical K 1 value. K IC, fractures will grow unstably. At stress-intensity levels considerably below K IC but above a minimal value known as the “stress-corrosion limit”, crack growth occurs progressively. This limit, which is expected based on thermodynamic considerations (e.g. Reference SegallSegall, 1984), has not been unambiguously detected in the laboratory, because practical limitations seldom permit K 1 to be less than ~0.6K IC. Indirect estimates of the stress-corrosion limit in rocks (Reference SegallSegall, 1984) suggest that it is above ~1/3K IC. Because of the relatively modest deviatoric stresses typically arising subglacially, I wish to lake into account a finite stress-corrosion limit to calculate crack-growth rates, v e, by using the following expression that is consistent with sub-critical crack-growth data (e.g. Reference AtkinsonAtkinson, 1987):

where v
1 and γ are material parameters obtainable graphically from a plot of crack-growth rate v
c (on a logarithmic scale) vs ![]() , once K
IC is known (e.g. Reference Walder and HalletWalder and Hallet, 1985). Equation (12) converges with the simpler expression commonly used for empirical data well above the stress corrosion limit (Reference AtkinsonAtkinson, 1987):
, once K
IC is known (e.g. Reference Walder and HalletWalder and Hallet, 1985). Equation (12) converges with the simpler expression commonly used for empirical data well above the stress corrosion limit (Reference AtkinsonAtkinson, 1987):
where m is 40 ± 10 and ξ is a constant dependent on rock type.
Because tensile Stresses are highest at the rock surface directly up-glacier of the ice contact zone, and are aligned in the ice-flow direction and parallel to the floor of the subglacial cavity, cracks are most likely to originate there and grow transverse to ice flow. Observations of ledges and joint sets exposed by the recent retreat of Grinnell Glacier suggest that quarrying there is the product of fracture propagation that is strongly favored both along and perpendicular to bedding planes. It is, therefore, reasonable to assume that near-surface cracks would propagate downward normal to the surface and to the sliding direction until they encounter a relatively weak zone parallel to the bedding; crack growth could then accelerate along the bedding plane. This would then liberate a rectangular block from the loaded corner of a ledge (Fig. 1b) and redefine the ledge riser slightly up-glacier of its previous position.
The volume of rock freed from the bed per unit length transverse to ice flow is simply the height of the ledge times the ice contact area (L – S). Quarrying events are likely to be sporadic because long periods of slow crack growth would generally be necessary before fractures completely isolate a bedrock block. Assuming that crack propagation is rate-limiting, the long-term average volume of rock quarried per unit time, per unit distance transverse to the ice-flow direction would be ![]() (the bar represents an average). Dividing this by the ledge length yields the long-term quarrying rate averaged over the entire bed:
(the bar represents an average). Dividing this by the ledge length yields the long-term quarrying rate averaged over the entire bed:

Due to competing effects, crack-growth rates may not vary a great deal as they propagate: the stress-intensity factor increases with crack size, c, but diminishes with distance from the ice rock interface as the far-field tensile stress decreases. A first-order estimate can be obtained by simply substituting ve evaluated at the ice/rock interface for the average in Equation (14). I emphasize that this estimate becomes progressively poorer as cracking proceeds, because the growing crack increasingly influences the state of stress in the rock, causing it to diverge from the assumed stress state.
Results
Calculated quarrying rates are illustrated in Figure 2 for two distinct rock types for which relatively good data exist on sub-critical crack growth. They were obtained using Equations (14) and (12) with the material parameters used by Reference Walder and HalletWalder and Hallet (1985). The quarrying rate is such an extremely sensitive function of the state of stress in the bed, that quantitatively correct quarrying rates require knowledge of basal stresses with unrealistically high precision. Henee, the calculated quarrying rates should not be viewed as quantitatively reliable; rather, they serve as physically based indices of quarrying rate useful in defining the influence of glaciological parameters.

Fig. 2. Calculated index of quarrying rate as a function of sliding velocity and basal effective pressure. Model parameters were ledge width: L = 10 m; tread slope: sin β = 0.2; and cavity closure-rate constant: 5 a−1 M PA−3, which reflects standard rheological parameters (Reference PatersonPaterson, 1981). Empirical fracture-mechanical data (from Reference Walder and HalletWalder and Hallet, 1985) were used for: (a) Westerly Granite with 20 mm cracks, and (b) Sl Pons Marble with 10 mm cracks.
For the glacier and bed conditions represented in Figure 2, the model yields quarrying rates that are negligible outside a relatively narrow Pe range of 0.1–1 MPa. Starting with high P e conditions that are unfavorable for extensive ice/bed separation, the calculated crack-propagation rate increases dramatically with decreasing P e because of the resulting expansion of cavities that, in turn, concentrates the effective ice load (σ n – Pw) on ledge corners. Quarrying rates peak under conditions of extensive cavitation, with P e typically ranging from 0.1 to 1 MPa, while ice-induced loads are curtailed to the highest value dictated by ice strength. These rates appear reasonable as they range up to a fraction of a meter per year under optimal conditions, which is consistent with maximal inferred erosion rates (Reference Hallet, Hunter and BogenHallet and others, 1996). At very low to vanishing values of P e, the quarrying rate must diminish to zero because the area of the bed influenced by high ice loads vanishes, while the ice bed contact stress remains at the finite level dictated by ice strength. Where P e reaches zero over much of the bed, no quarrying is expected because the glacier would effectively float.
No ideal data set is available in test the principal model results, that quarrying is particularly active for conditions of small but finite effective pressure and high sliding velocity (Fig. 2). Such conditions have been well documented for several fast moving glaciers, including Variegated Glacier (Reference Humphrey and RaymondHumphrey and Raymond, 1994), Columbia Glacier (Reference Humphrey, Kamb, Fahncstock and EngelhardtHumphrey and others, 1993) and Ice Stream B (Reference Engelhardt, Humphrey, Kamb and FahnestockEngelhardt and others, 1990). Characteristics of these glaciers may have little relevance to the quarrying model, however, because considerable data suggest that they are underlain not by bedrock but by a deformable debris layer. A relatively deformable till layer, such as that inferred to underlie Ice Stream B (e.g. Reference Alley, Blakenship, Bentley and RooneyAlley and others, 1986), would effectively shield the rock from the direct action of the glacier and inhibit the formation of subglacial cavities, rendering quarrying unlikely. Nevertheless, I wish to Stress that the nature of the bed of any glacier is generally only known from rather sparse information, henee undeformable bedrock may underlie significant parts of these glaciers. Moreover, one can argue for the occurrence of substantial areas of eroding bedrock under glaciers overriding a debris layer over bedrock, because an active and distributed source of sediment is required to sustain a deforming layer of debris. Keeping this in mind, I cautiously examine relevant data from Variegated and Columbia Glaciers.
Conditions of small but finite effective pressure and high sliding velocity, which favor rapid quarrying, were well documented during the surge of Variegated Glacier by Reference Humphrey and RaymondHumphrey and Raymond (1994). There the sediment flux in proglacial streams is consistent with extreme erosion rates amounting to about 0.5 m per 17 year surge cycle (Reference KambKamb and others, 1985; Reference Humphrey and RaymondHumphrey and Raymond, 1994). This flux includes a rough estimate of bedload that makes up about half of the total sediment yield, and is presumably composed largely of quarried material. They estimated that two-thirds of this sediment was delivered to the glacier front during the surge (1–2 years), but had no information on when the sediment was produced subglacially. As conditions for quarrying are particularly favorable during the surge, while being singularly unfavorable between surges because of slow sliding and relatively high P e, it is reasonable to infer that the surge is a period of both exceptionally high sediment yields and rapid erosion. With this inference, the corresponding short-term valley-wide quarrying rates are likely to be on the order of 0.1 m a−1 during the surge. These rates are in accord with model values of maximum quarrying rates, assuming that quarrying is responsible for a large proportion of the sediment production.
The normal stress required for significant fracture of a loaded ledge corner is approximately 5 M Pa for many lithologies. Such values are reached where cavities separate approximately 90% of the bed from the ice, a condition that arises for sliding at 100 m a at effective pressures of 0.2 and 0.7 M Pa for ledges 10 and 1 m apart, respectively. Such low effective pressures are not unreasonable even under thick glaciers where overburden pressures approach 10 M Pa. For example, measurements at Variegated Glacier (Reference KambKamb and others, 1985) and Columbia Glacier (Reference Humphrey, Kamb, Fahncstock and EngelhardtHumphrey and others, 1993) suggest that very rapid ice motion can be associated with P e < 0.1 M Pa. Thus, at least for these glaciers, periods of fast basal motion and extremely low P e, which are conducive to rapid erosion according to the model, are indeed plausible.
Quarrying Under Non-Steady Conditions
Substantial temporal variations in crack-growth rates are expected in part because subglacial water-pressure variations, which are common (Reference Engelhardt, Harrison and KambEngelhardt and others, 1978; Reference KambKamb and others, 1985), cause changes in the normal stress on rock surfaces and transient pore-pressure gradients in the bedrock. The dependence of crack-growth rates on deviatoric stresses is so sensitive that crack growth during brief periods with conditions favorable for cracking is likely to be important. This would include periods during which (1) P e is in the critical 0.1–1 M Pa range: (2) water pressure drops abruptly, causing a large transient increase in (σ n – P w) (e.g. Reference IversonIverson, 1991); and (3) deviatoric stresses are temporarily enhanced by the passage of a clast in forceful contact with the bed.
The importance of short-duration stress events for the long-term average crack propagation rate (e.g. Reference LliboutryLliboutry, 1965) can be demonstrated easily. Consider a crack that propagates at a constant rate v 0 due to a steady imposed tensile stress σ 0. I now determine the average rate at which that crack will grow assuming the ledge is exposed for short durations to a stress σ * that exceeds σ 0. The length of a crack at time t is

where N and t * are the number and duration of load events, and v * is the crack-growth rate during high-stress periods. Using the simpler expression for the instantaneous crack-growth rate (Equation (13)), the time-averaged crack-growth rate is

Because m is so large (m ~ 40), short-duration stress perturbations, even if very infrequent, could significantly affecl the long-term crack-grow in rate. For example, taking (ft*/t) to be 10−4, which corresponds roughly to a single 1 h stress event per year, would double vc for a stress perturbation only 25% above the steady value.
Rapid drops in basal water pressure of up to 1 or 2 M Pa recorded in glacier boreholes (Reference Engelhardt, Harrison and KambEngelhardt and others, 1978; Reference KambKamb and others, 1985) are particularly interesting in this context. Assuming that such records reflect comparable declines in water pressure at particular sites on the bed, the support of the glacier provided by-basal water would be temporarily reduced, thereby increasing the ice load on the bedrock near these sites. Importantly, the increase in normal stress on the bedrock can greatly exceed the drop in water pressure. For extensive cavities expected under very low effective pressures, the transient increase in normal stress can be related simply to the extern of cavitation S′ and the magnitude of the water-pressure drop: Δσ n = ΔP w(1 – S′). Thus, for example, for cavities covering 90% of the bed, a 1 M Pa drop in water pressure would theoretically increase the normal stress by 9 M Pa. Although such high-stress events would be short-lived because the cavities would contract rapidly, they are likely to figure importantly in subglacial rock, fracture by elevating the deviatone stresses into regions of very rapid crack growth. Temporal variations in water pressure are also central to Reference Röthlisberger and IkenRöthlisberger and Iken’s (1981) model of debris entrainment and Reference IversonIverson’s (1991) analysis of quarrying. However, in contrast with both Iverson’s and my model, Röthlisberger and Iken’s work stresses the importance of rapid increases in water pressure that cause drops in normal stress, thereby inducing supercooling and basal freezing.
I note that the finite strength of ice moderates the magnitude of stress transients. For the configuration of loads shown in Figure 1, the stress ceiling σn * (~ 10 M Pa, as discussed earlier) severely limits the contact stresses under conditions of extreme cavitation, particularly during transient increases in effective stresses.
Concluding Remarks
I have examined a simple scenario in which ice-induced stresses can cause sub-critical crack growth permitting detachment of bedrock fragments, and have developed a physically based functional relationship between quarrying rate and glaciological parameters. Low effective basal pressures (0.1 – 1 M Pa) and fast sliding emerge as the dominant glaciological conditions favoring glacial quarrying because they induce extensive ice/bed separation and highly concentrated stresses where ice contacts the bed. This result is consistent with data reflecting rapid erosion by fast moving glaciers with low basal effective stress.
The results I have obtained to date are promising in that they contain much of the important physics and are able to produce reasonable quarrying rates in all rocks, as long as they contain microcracks on the order of 1–10 mm in length. My theoretical study to date provides strong motivation for incorporating results from Reference IversonIverson’s (1991) detailed analysis of stresses near ledge cornera to further develop the quarrying model. This would generalize the model to include potential crack growth closer to step corners, rather than only up-glacier from where ice regains contact with the bed, and under a broader range of conditions owing to the tendency for normal stresses to focus at the corners. This generalization would render the model less restrictive because it would considerably broaden the range of basal conditions conducive to active quarrying. Other promising goals are to integrate the quarrying model with models of other erosion processes, and to seek field validation.
One troubling aspect of the present model formulation is that quarrying rates depend on basal stresses in such an extremely sensitive fashion that quantitatively correct quarrying rates require knowledge of basal stresses with unrealistically high precision. Hence, the calculated quarrying rates should not be viewed as being quautitatively reliable; rather, they serve as physically based indices of quarrying rate useful in defining the influence of glaciological parameters. This characteristic renders it difficult to use the model in simulations of landform development (e.g. Reference Oerlemans.Oerlemans, 1985; Reference Harbor, Hallet and RaymondHarbor and others, 1988) or of glacial denudation, because basal conditions cannot be defined precisely. The latter renders studies of sediment yield from glacial catchments the most promising source of quantitative information on erosion rates. However, much of this extreme sensitivity is artificial; it reflects the highly idealized perfectly periodic bed geometry and the treatment of water pressure as being uniform over the bed. Promising model improvements that would moderate the present model sensitivity include: (1) a more realistic bed geometry with a spectrum of roughness elements; (2) spatially non-uniform σ n and P w; and (3) explicit treatment of transient effects due to pore-pressure variations in arrays of bedrock microcracks, as suggested by Reference IversonIverson (1991).
Acknowledgements
It is a pleasure to acknowledge insightful discussions I have had regarding aspects of glacial quarrying with R.LeB. Hooke, N. Humphrey, N. Iverson, Y. Merrand and R. Shreve. I thank T. Bennett, K. Cuffey, W. Haeberli, R.LcB. Hooke, N. Iverson, Y. Merrand, R. Powell and M. Sharp for very useful editorial comments. This work was sponsored by the U.S. National Science Foundation (EAR 90-05069).



