How well can we parameterize past accumulation rates in polar ice sheets?

Abstract

An important component of models of the cryosphere is the calculation of accumulation rates over polar ice sheets. As a first-order approximation, many models rely on the assumption that temperature is the main controlling factor for precipitation. However, compilation of available ice-core data, including a new core from Taylor Dome, East Antarctica, suggests that precipitation is significantly decoupled from temperature for a large proportion of both the Greenland and Antarctic ice sheets. While the estimated glacial-to-interglacial change in temperature does not differ greatly among ice cores from each ice sheet, the estimated change in accumulation rate varies by more than a factor of 2. A simple vapor-pressure parameterization gives reasonable estimates of accumulation in the ice-sheet interior, but this is not necessarily the case close to the ice-sheet margin, where synoptic weather systems are important.

Introduction

In recent years, much effort has been devoted to the development of models that can accurately simulate modern accumulation patterns over polar ice sheets (e.g. Fortuin and Oerlemans, 1990; Bromwich and others, 1993; Fastook and Prentice, 1994). There has also been an effort to estimate the magnitude of accumulation-rate changes under future greenhouse-warming scenarios (e.g. Huybrechts and Oerlemans, 1990; Verbitsky and Saltzman, 1995; Verbitsky and Oglesby, 1995). Somewhat less emphasis has been placed on the calculation of accumulation under past climate conditions. Such research is important because accumulation is one of the determining factors in ice-sheet response to climate. Althougli numerical models of former ice-sheet configurations have been developed, comparison of these results with glacial-geologic data (e.g. Stuiver and others, 1981; Denton and others, 1989; Bromwich and others. 1991; Huybrechts, 1993) does not provide sufficient validation alone (Oreskes and others, 1994).

Accumulation rate is one of the fundamental parameters available from analysis of ice cores in polar regions. As the areal coverage and quality of ice-core records increases, it becomes increasingly worthwhile to consider the extent of agreement between model estimates and empirical measurements. In this paper, common approaches to the parameterization of accumulation rates on polar ice sheets are reviewed, and these approaches are discussed in the light of ice-core data from both hemispheres. Such comparisons provide an important lest of the fidelity of numerical models.

Parameterization of Accumulation in Numerical Models

The most straightforward approach to modeling accumulation over polar ice sheets is to assume that precipitation is primarily thermodynamically controlled. That is, the amount of water precipitated is proportional to the moisture-carrying capacity of the air mass, according to the relationship between temperature (T) and the saturation vapor pressure (P) over ice, which follows an Arrhenius relationship:

(1)

where α,β and care empirical constants. Note that for polar ice sheets, other than very near the margin, it may be assumed that ablation is minimal and that accumulation ≈ precipitation.

Over large parts of Antarctica there is a strong correlation between accumulation rate, P and T above the surface inversion layer (Robin, 1977). The correlation can be improved further by accounting empirically for orographic effects, for example, Fastook and Prentice (1994) use the observed present-day Antarctic accumulation pattern to determine a function relating accumulation rate (b) to the average surface slope (S) and the saturation vapor pressure:

(2)

where, A, B and C are empirical constants. Fortuin and Oerlemans (1990) and Huybrechts (1993, 1994) take a more direct approach, expressing simply as an empirical function of mean annual temperature:

(3)

In modeling modern accumulation rates over the Greenland ice sheet, Bromwich and others (1993) take a considerably more sophisticated approach, using empirical measures of atmospheric dynamics:

(4)

where H is the terrain height, and V _G and V _v are parameterizations for the geostrophic- and vertical-wind velocity, respectively. In Equation (4), as in Equations (2) and (3), P may be considered an empirical function of T.

Clearly, if we wish to apply models such as those given above to past climate conditions, we will be limited by the assumption that the empirically derived coefficients (and in the case of Equation (4), the atmospheric dynamics) remain constant. Because of this inherent limitation of empirical models, we may consider turning to more sophisticated atmospheric general circulation models (GCMs), which explicitly solve for synoptic-scale variables such as storm frequency. Current-generation GCMs, however, are notoriously poor at simulating precipitation in polar regions, tending to produce higher-than-observed accumulation rates over both Greenland and Antarctica (Gates and others, 1990; Tzeng and others, 1993; Bromwich and others, 1994). The discrete nature of precipitation events is in contrast to such climate variables as pressure and temperature, for which long-term annual average values provide resolution sufficient for many applications. This problem has not been resolved, but must, in part, be a consequence of the inability of these models to simulate adequately cyclonic systems (Bromwich and others, 1991; Connolley and Cattle, 1994) and to incorporate fully the seasonal cycle (Joussaume and Jouzel, 1993; Charles and others, 1994).

In summary, we are currently limited to “low-order” empirical models, which can be tuned to fit observed accumulation patterns to an arbitrary degree of accuracy, but are limited in their ability to simulate temporal changes; or to “high-order” GCMs that are currently unsatisfactory for modeling polar precipitation. A possible way around this dilemma is to assume that the changes in the climate variables predicted by a GCM are more precise than the absolute values predicted (e.g. Kutzbach and Guetter, 1986; COHMAP members, 1988; Verbitsky and Sahzman, 1995). However, such an approach still requires empirical observations for scaling the model-output data, for the immediate future at least, we will be reliant on empirical models, and it is therefore important to consider the extent of agreement between the predictions of such models and the paleo-climate record from ice cores.

Data

In reviewing empirical measurements of accumulation rate, the transition from the Last Glacial Maximum (LGM) (about 20 ka BP) to the Holocene is considered, since it represents the largest climate change for which there is a reasonable ice-core dataset available.

For the Vostok ice core (Fig. 1), East Antarctica, Lorius and others (1985) estimated accumulation rates over the last 150 000 years by assuming, as in the models discussed above, that accumulation is thermodynamically controlled. the temperature history is taken from isotopic measurements (δ ¹⁸O or δD) according to:

(5)

where T is the temperature above the surface inversion layer, and a and b are constants. Taking into account changes in the isotopic content of sea water in the calculation of T, and using a = 9‰°C⁻¹ for δD (Jouzel and others, 1996), this parameterization gives a LGM lowering of accumulation at Vostok to about 50% of the present-day value. It should be noted that borehole temperature measurements at Vostok (Salamatin and others, 1994) suggest that the assumption of a constant δ − T relationship is probably reasonable for the East Antarctic interior. That the original Vostok time-scale (Lorius and others, 1985) compares favorably with recent and more accurate determinations of the Voslok age-depth relationship Jouzel and others, 1993; Sowers and others, 1993; Sowers and Bender, 1995) supports the validity of this parameterization, at least in central East Antarctica. It is further supported by ¹⁰Be measurements in the Vostok core, which show a 50%-60% decrease in concentration following the LGM (Raisbeck and others, 1987; Jouzel and others, 1989). A strong inverse correlation between snow accumulation and ¹⁰Be concentration is expected because ¹⁰Be deposition at low-accumulation-rate sites such as Vostok is predominantly by dry fallout (Raisbeck and Yiou, 1985; Yiou and others, 1985; Lorius and others, 1989; Steig and others, in press); also the polar atmospheric concentration of ¹⁰Be is unlikely to have changed by more than a few percent over the last 20 ka (Steig and others, 1996).

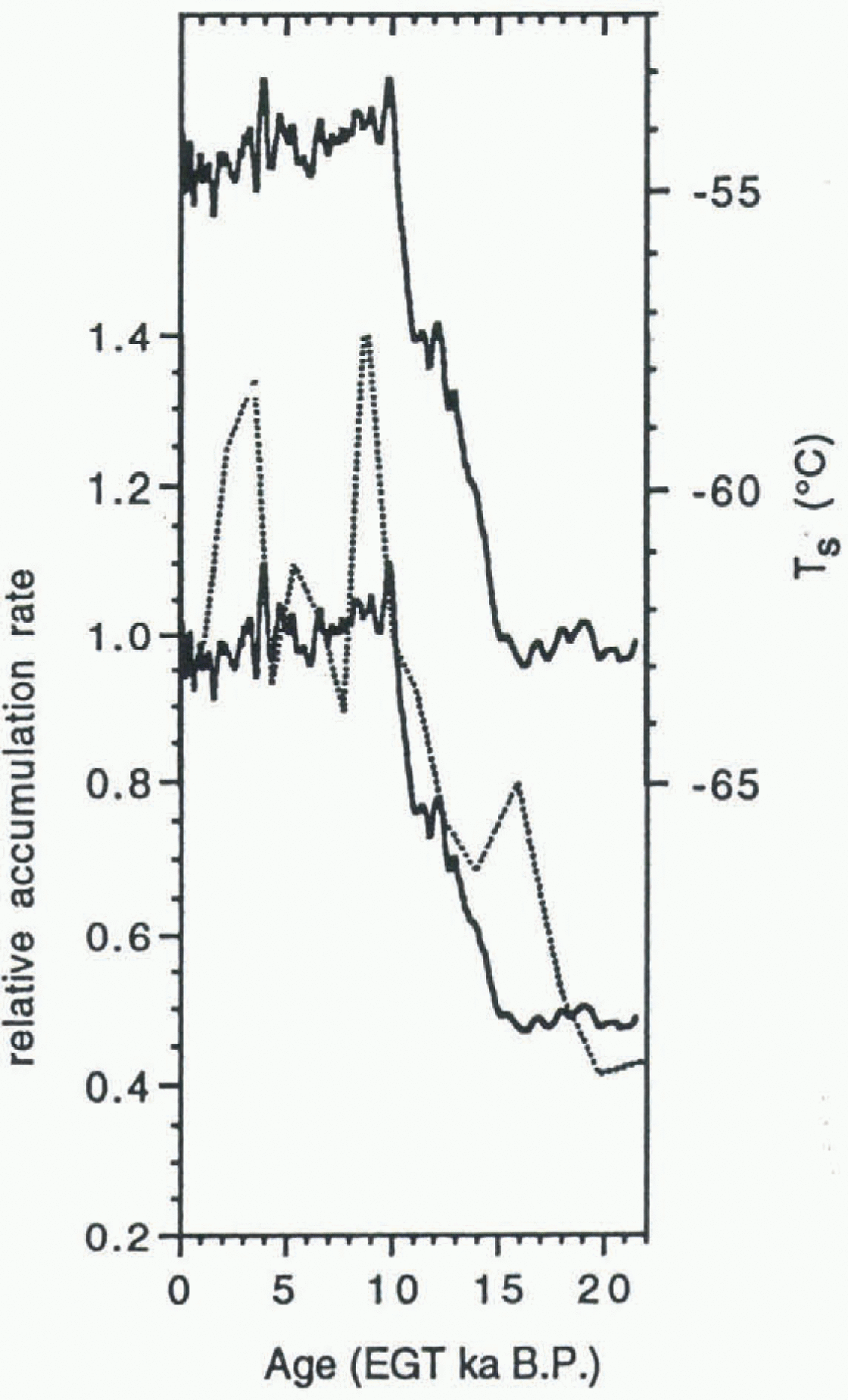
Fig. 1. Upper line: surface temperature at Vostok, Antarctica, over the last 25 ka on the “extended glaciological time-scale” (EGT) (Jouzel and others, 1993). Lower solid line: the relative accumulation rate (normalized to a modern value of 1) calculated from the vapor-pressure relationship (Lorius and others, 1985). Dotted line: the relative accumulation rate calculated from¹⁰ Be concentrations (Raisbeck and others, 1987).

The best estimates of accumulation rates in Greenland are derived from combined ice-flow model layer-thickness measurements on the U.S. and European ice cores at Summit (GISP2 and GRIP; respectively). Dahl-Jensen and others (1993) calculated that accumulation rates at the GRIP site were about 30% of present-day values at the LGM; Cutler and others (1995) and Cuffey and Close (in press) give very similar estimates of the LGM accumulation rate at GISP2 (30 km away).

For many other Greenland ice cores, particularly those closer to the coast, the estimated LGM-Holocene change in accumulation rate is larger than at Summit. Depending on the time-scale adopted and the flow-model assumptions employed, the LGM accumulation rate at Gamp Century, northwest Greenland, was as low as 20% of the Holocene value (Reeh, 1990). Similar estimates have been obtained for the southwestern Greenland site, Dye3 (Reeh and others, 1985; Reeh, 1990), while a LGM lowering of accumulation to as little as 10% of present values was calculated for the Devon Ice Cap, eastern Arctic Canada (Paterson and Waddington, 1984).

In Antarctica, as in Greenland, warmer, less continental sites appear to have experienced a somewhat larger change in accumulation rates during the LGM-Holocene transition. While accumulation-rate histories at Dome Cirque and Dome R (interior East Antarctica) are apparently similar to those at Vostok (Jouzel and others, 1989; 1995), estimates from ¹⁰Be measurements (Beer and others, 1987) and from recent refinements to the age-depth relationship (Hammer and others, 1994) suggest that accumulation rates at Byrd Station, West Antarctica, during the LGM were at most 40% of Holocene values. At Taylor Dome (Fig. 2), just inland of the Transantarctic Mountains in East Antarctica (Grootes and Steig, 1992; Waddington and others, 1993; Grootes and others, 1994), there is an even greater LCM-Holocene contrast: both preliminary flow-model calculations and ¹⁰Be measurements (Steig, 1996) indicate that the accumulation rate during the LGM was at most 20-25% of the Holocene value.

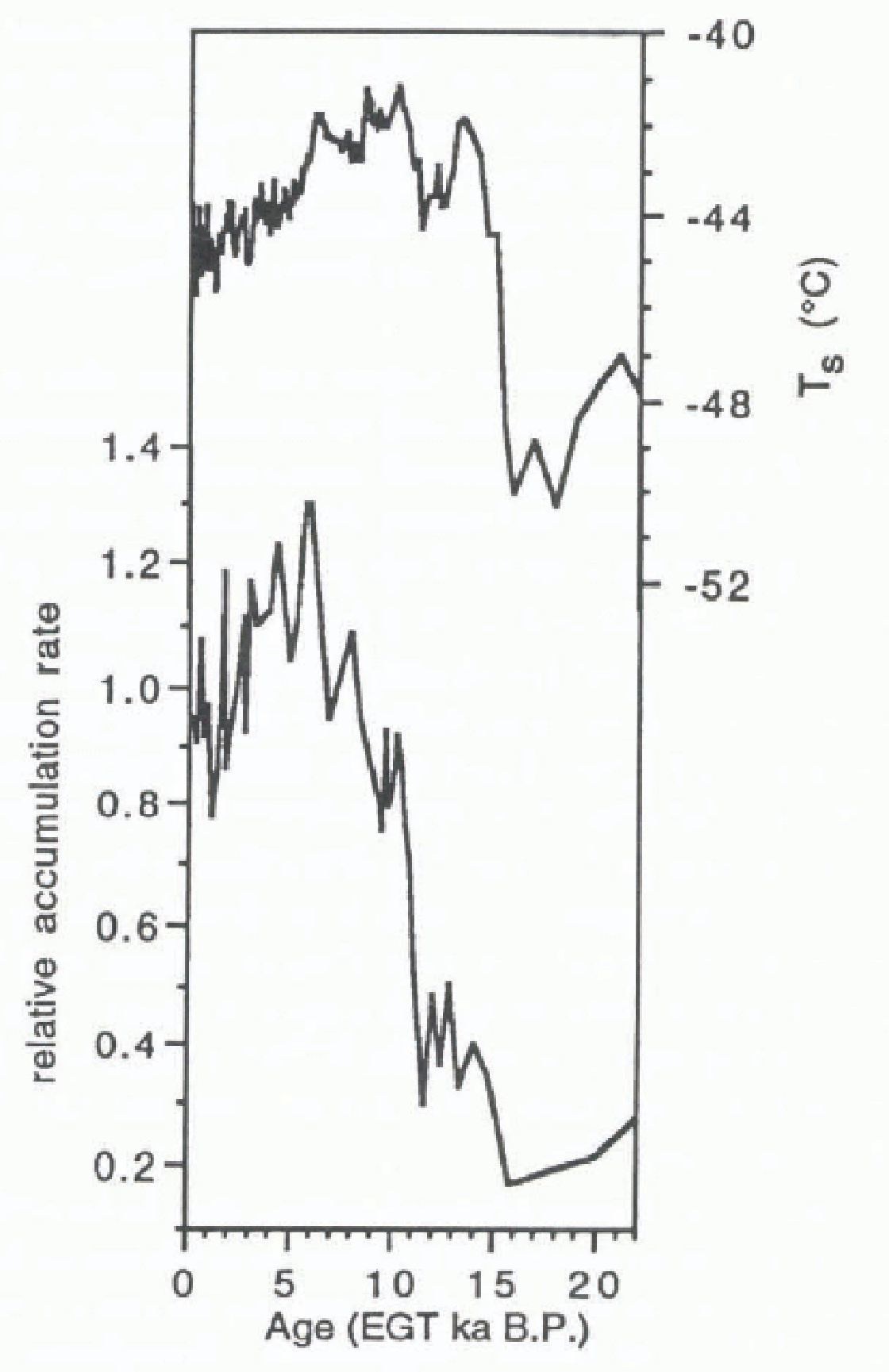
Fig. 2. Upper line: surface temperature at Taylor Dome, Antarctica, calculated from δ¹⁸O measurements at Taylor Dome, assuming that δ¹⁸O = 8 δD+ 10 and ∂δD/∂T = 9‰/°C (after Jouzel and others, 1996). Lower line: relative accumulation rate from ¹⁰Be measurements (Steig, 1996).

Comparison of Model Results and Ice-Core Data

Analysis of borehole temperature measurements in the Summit cores (Cuffey and others, 1994, 1995; Johnsen and of others, 1995) reveal that the slope of the δ ¹⁸ O-T relationship (the value of a in Equation (5)) in central Greenland is much lower (~0.2) for the LGM-Holocene transition than the modern value of about 0.6. Thus, we cannot use the same parameterization for the Summit cores as given above for Vostok. However, assuming that the thermodynamic relationship applies at Summit, the surface-temperature history derived from borehole analyses yields an accumulation profile that is highly compatible with the inferred history from ice-flow modeling (Cuffey and Clow, in press). These results are shown in Figure 3. The assumption has been made that accumulation is most highly correlated with the temperature above the surface inversion layer T _i(K), which can be estimated from the surface temperature T _s (Fortuin and Oerlemans, 1990):

(6)

Fig. 3. Upper line: surface temperature at Summit, Greenland, calculated from borehole temperatures and δ¹⁸O values (Cuffey and others, 1995). Lower solid line: relative accumulation rate calculated from the vapor-pressure relationship (Lorius and others, 1985). Dotted line: flow-model calculations of accumulation (Cuffey and Clow, in press).

Given the strong apparent correlation between accumulation and temperature at both Summit and at Vostok, it is tempting to conclude that accumulation rates over polar ice sheets can generally be parameterized in terms of a simple thermodynamic relationship (Equation (1)). However, results from the Taylor Dome core bring this into question. As illustrated in Figure 2, accumulation at Taylor Dome does not parallel the temperature history inferred from δ ¹⁸O analyses. Although Taylor Dome appears Ito have experienced a somewhat different temperature hisiory than did Vostok, it is likely that the δ − T relationship is similar at both sites, given the similarity in the magnitude and timing of the LGM-Holocene shift in stable-isotope values (Grootes and others, 1994) and the probable similarity in moisture provenance (Petit and others, 1991; Mayewski and others, 1996). The noticeable differences between the inferred temperature and accumulation histories at Taylor Dome strongly imply that non-thermal effects, such as the degree of storminess, must play a role in determining accumulation at Taylor Dome. Although the differences are not as dramatic, a similar argument applies to the Byrd results, and probably to the Gamp Century, Dye3 and Devon Island cores: in general, the magnitude of temperature change during the LGM-Holocene transition is comparable among cores on each ice sheet, but the estimated accumulation-rate change varies by al least a factor of 2.

A more favorable comparison between data and model results can be obtained if empirical fits to the modern distribution of accumulation are used, rather than the simple parameterization given in Equation (1). Common to each of the models discussed above (Equations (2) and (3)) is that the sensitivity of accumulation rate to temperature change decreases with distance from the ice-sheet margin, bearing in mind that the mean annual temperature (T) in all three models is a function of latitude and altitude. (That is, the derivatives ∂b/∂T of each expression for increase with T over an appropriate range of temperatures. For example, if we postulate a decrease in T of 10°C and assume that all other parameters remain constant, we calculate from the Huybrechts (1993) model (Equation (3)) that a site with a current T of −30°C (e.g. Byrd Station) would experience a drop in accumulation to about 50% of present-day values. A site with current of −55°C (e.g. Vostok) would experience a much smaller (about 10%) decrease in accumulation. The values given by Fastook and Prentice (1994) for the coefficients in Equation (1) yield similar results, as does Bromwich and others' (1993) model for Greenland. Note, however, that while the sign of the calculated difference in response is correct, these parameterizarions greatly overestimate the difference among ice-core sites, suggesting that the assumption of constant coefficients is invalid.

Conclusions

In general, it appears that the accumulation history of the interior of large ice sheets is quite reasonably approximated by a simple thermodynamic relationship:

(7)

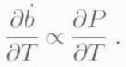
Although this conclusion is in agreement with the early work of Robin (1977) and Lorius and others (1985) in Antarctica, it is in marked contrasl to that of Kapsner and others (1994), who suggested that atmospheric circulation, rather than temperature, drives accumulation-rate variations at Summit, Greenland.

Away from the ice-sheet interior, however, neither the simple relationship given above, nor empirical parametcrizations of the distribution of accumulation under modern conditions, can be used to determine reliably past accumulation rates. Results from ice cores such as Taylor Dome and Byrd in Antarctica, and Camp Century and Dye3 in Greenland, suggest that changes in atmospheric circulation, and possibly other factors, must play a major role in determining regional accumulation patterns.

Finally, it is importanl to note that empirical models such as those of Huybrechts 1993 and Fastook and Prentice (1994), in which T is the only free variable, tend to over-estimate the difference in sensitivity of interior and coastal areas with regard to accumulation rate during colder-than-prescnt climates. Inaccuracies of this nature suggest that numerical models of ice-sheet configuration that use simple thermodynamic relationships in their parameterization of accumulation rate must be treated with caution.