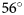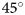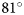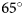Introduction
Icebergs are fragments of frozen freshwater calved from a glacier, ice sheet, or ice shelf. Iceberg calving is a variable in the glacial mass balance of marine-terminating glaciers that is associated with high uncertainties (Bigg and others, Reference Bigg, Wadley, Stevens and Johnson1997; Enderlin and others, Reference Enderlin2014; Amaral and others, Reference Amaral, Bartholomaus and Enderlin2020; Alley and others, Reference Alley2023). By releasing freshwater icebergs may alter marine currents and nutrient concentrations (Azetsu-Scott and Syvitski, Reference Azetsu-Scott and Syvitski1999; Dierking and Wesche, Reference Dierking and Wesche2014; Moon and others, Reference Moon2018; Sutherland and others, Reference Sutherland2019; Rezvanbehbahani and others, Reference Rezvanbehbahani, Stearns, Keramati, Shankar and Van Der Veen2020). Iceberg above-waterline areas are essential for iceberg drift and deterioration modeling (Keghouche and others, Reference Keghouche, Counillon and Bertino2010; Marchenko and others, Reference Marchenko, Diansky and Fomin2019; Monteban and others, Reference Monteban, Lubbad, Samardzija and Løset2020), to approximate marine freshwater fluxes (Sulak and others, Reference Sulak, Sutherland, Enderlin, Stearns and Hamilton2017; Moon and others, Reference Moon2018; Moyer and others, Reference Moyer, Sutherland, Nienow and Sole2019; Rezvanbehbahani and others, Reference Rezvanbehbahani, Stearns, Keramati, Shankar and Van Der Veen2020; Schild and others, Reference Schild, Sutherland, Elosegui and Duncan2021; Shiggins and others, Reference Shiggins, Lea and Brough2023), and nutrient fluxes (Bhatia and others, Reference Bhatia2013; Duprat and others, Reference Duprat, Bigg and Wilton2016). Maritime engineering and operational ice charting need iceberg size distributions for safe Arctic operations (Bobby and Power, Reference Bobby and Power2023). The area-frequency distribution of iceberg populations can be typically described by a power-law distribution near the calving front, and by a log-normal distribution in open water (Kirkham, Reference Kirkham2017).
Satellite remote sensing is invaluable for retrieving iceberg areas (Sulak and others, Reference Sulak, Sutherland, Enderlin, Stearns and Hamilton2017; Moyer and others, Reference Moyer, Sutherland, Nienow and Sole2019; Neuhaus and others, Reference Neuhaus, Tulaczyk and Branecky Begeman2019; Scheick and others, Reference Scheick, Enderlin and Hamilton2019). Though, errors in the observed iceberg areas can lead to skewed size distributions (Scheick and others, Reference Scheick, Enderlin and Hamilton2019) and propagate into estimates upon the iceberg areas.
Satellite synthetic aperture radar (SAR) data are often used to detect icebergs (Power and others, Reference Power, Youden, Lane, Randell and Flett2001; Dierking and Wesche, Reference Dierking and Wesche2014; Marino and others, Reference Marino, Dierking and Wesche2016; Tao and others, Reference Tao, Doulgeris and Brekke2016; Soldal and others, Reference Soldal, Dierking, Korosov and Marino2019; Færch and others, Reference Færch, Dierking, Hughes and Doulgeris2023) due to their independence from weather and solar illumination. Buus-Hinkler and others (Reference Buus-Hinkler, Qvistgaard and Krane2014) showed for Sentinel-1 SAR data with reference to optical Landsat data that iceberg areas retrieved from the SAR data are inaccurate. The error in the iceberg area retrieval from SAR can be partly, however not fully, explained by the limit in the spatial resolution (Buus-Hinkler and others, Reference Buus-Hinkler, Qvistgaard and Krane2014). The high resolution of currently available non-commercial optical satellite data, low noise levels, the absence of SAR speckle, and the less variable and less ambiguous signals of ocean and ice surfaces are advantages of these data. Here we argue for leveraging the growing archive of high resolution SAR data for the iceberg area retrieval supported by higher resolution optical data. However, this requires understanding errors in the iceberg area retrieval from optical satellite data.
Low sun angles at high latitudes challenge the iceberg area retrieval from optical satellite data. The European Space Agency (2019) recommends using Sentinel-2 data acquired below a solar zenith angle (Fig. 1) of $70^\circ$![]() . While some studies limited the iceberg area retrieval accordingly, we recognize the need to maximize the temporal bounds. Moyer and others (Reference Moyer, Sutherland, Nienow and Sole2019) used Sentinel-2 data acquired above a solar zenith angle of $70^\circ$
. While some studies limited the iceberg area retrieval accordingly, we recognize the need to maximize the temporal bounds. Moyer and others (Reference Moyer, Sutherland, Nienow and Sole2019) used Sentinel-2 data acquired above a solar zenith angle of $70^\circ$![]() , adjusting the threshold to the different illumination conditions. On sea ice, Kern (Reference Kern2022) recognized inconsistencies due to varying illumination conditions in Landsat data already below a solar zenith angle of $65^\circ$
, adjusting the threshold to the different illumination conditions. On sea ice, Kern (Reference Kern2022) recognized inconsistencies due to varying illumination conditions in Landsat data already below a solar zenith angle of $65^\circ$![]() . The literature appears unclear regarding a sensible illumination limit for the iceberg area retrieval from optical satellite data. In this paper we therefore address the impact of the varying solar illumination on the iceberg area retrieval from Sentinel-2 near-infrared data.
. The literature appears unclear regarding a sensible illumination limit for the iceberg area retrieval from optical satellite data. In this paper we therefore address the impact of the varying solar illumination on the iceberg area retrieval from Sentinel-2 near-infrared data.

Figure 1. Solar angles and viewing geometry of a passive satellite sensor with respect to an iceberg on a target plane. The paper focuses on the variation in the solar zenith angle, which is a function of the time of the day, the time of the year, and the latitude.
Optical remote sensing of Arctic icebergs
Many have detected and delineated icebergs in optical satellite data across spatial and temporal scales (Williams and Macdonald, Reference Williams and Macdonald1995; Kirkham, Reference Kirkham2017; Sulak and others, Reference Sulak, Sutherland, Enderlin, Stearns and Hamilton2017; Moyer and others, Reference Moyer, Sutherland, Nienow and Sole2019; Neuhaus and others, Reference Neuhaus, Tulaczyk and Branecky Begeman2019; Scheick and others, Reference Scheick, Enderlin and Hamilton2019; Monteban and others, Reference Monteban, Lubbad, Samardzija and Løset2020; Rezvanbehbahani and others, Reference Rezvanbehbahani, Stearns, Keramati, Shankar and Van Der Veen2020). An early attempt used a segmentation approach in the first years of the Landsat mission (Williams and Macdonald, Reference Williams and Macdonald1995). It is most common to apply an absolute reflectance threshold to one or several spectral bands to detect icebergs observed in optical remote sensing data (Sulak and others, Reference Sulak, Sutherland, Enderlin, Stearns and Hamilton2017; Moyer and others, Reference Moyer, Sutherland, Nienow and Sole2019; Neuhaus and others, Reference Neuhaus, Tulaczyk and Branecky Begeman2019; Scheick and others, Reference Scheick, Enderlin and Hamilton2019; Rezvanbehbahani and others, Reference Rezvanbehbahani, Stearns, Keramati, Shankar and Van Der Veen2020). This approach is usually able to distinguish icebergs from open water, but icebergs may be confused with sea ice (Sulak and others, Reference Sulak, Sutherland, Enderlin, Stearns and Hamilton2017). A related approach exploits the contrast between the surrounding ocean and the iceberg (Kirkham, Reference Kirkham2017). Rezvanbehbahani and others (Reference Rezvanbehbahani, Stearns, Keramati, Shankar and Van Der Veen2020) showed that a convolutional neural network is less prone to false detections of highly reflective non-iceberg surfaces in ice mélange.
Iceberg areas are sensitive to the reflectance threshold used to detect and delineate icebergs in optical data. Scheick and others (Reference Scheick, Enderlin and Hamilton2019) found a sensible balance between true and false positive icebergs at a 0.19 reflectance threshold applied to panchromatic Landsat top-of-atmosphere (TOA) data acquired between May and October. With reference to Sulak and others (Reference Sulak, Sutherland, Enderlin, Stearns and Hamilton2017), Scheick and others (Reference Scheick, Enderlin and Hamilton2019) found overestimated total iceberg areas at varying magnitudes in different Greenlandic fjords. Moyer and others (Reference Moyer, Sutherland, Nienow and Sole2019) proposed a 0.13 reflectance threshold applied to TOA Sentinel-2 near-infrared (NIR) data. At a solar zenith angle of $47^\circ$![]() the study implies an average overestimation of iceberg areas by 4% with reference to higher resolution optical satellite imagery. Rezvanbehbahani and others (Reference Rezvanbehbahani, Stearns, Keramati, Shankar and Van Der Veen2020) adopted the 0.13 reflectance threshold to estimate marine freshwater fluxes.
the study implies an average overestimation of iceberg areas by 4% with reference to higher resolution optical satellite imagery. Rezvanbehbahani and others (Reference Rezvanbehbahani, Stearns, Keramati, Shankar and Van Der Veen2020) adopted the 0.13 reflectance threshold to estimate marine freshwater fluxes.
Solar angle effects on optical measurements of glacier ice, snow, water
Studying optical measurements of icebergs floating in open water primarily encounters three materials: Glacier ice, snow, and liquid water. Open water exhibits specular reflections and hence reflects about 0.5% of the downwelling shortwave radiation to a sensor (Pegau and Paulson, Reference Pegau and Paulson2001). The reflectance of open water rises steeply above solar zenith angles of about $70^\circ$![]() , with an increasing variation caused by wind speed (Pegau and Paulson, Reference Pegau and Paulson2001). Glacier ice and snow reflect strongly at visual and near-infrared wavelengths, and their reflectance decreases above ~600 nm (Warren, Reference Warren2019). At wavelengths between 500 nm and 1500 nm, the size and concentration of air bubbles and cracks drive the reflectance of glacier ice. Scattering occurs at the interface of the ice and the air bubbles. Thus, a higher concentration or size of these bubbles increases the reflectance (Gardner and Sharp, Reference Gardner and Sharp2010). The snow reflectance varies with the snow thickness, density, age, the air temperature, and the grain size. Contaminants such as dust or ash dampen the glacier ice and snow reflectance (Gardner and Sharp, Reference Gardner and Sharp2010; Warren, Reference Warren2019).
, with an increasing variation caused by wind speed (Pegau and Paulson, Reference Pegau and Paulson2001). Glacier ice and snow reflect strongly at visual and near-infrared wavelengths, and their reflectance decreases above ~600 nm (Warren, Reference Warren2019). At wavelengths between 500 nm and 1500 nm, the size and concentration of air bubbles and cracks drive the reflectance of glacier ice. Scattering occurs at the interface of the ice and the air bubbles. Thus, a higher concentration or size of these bubbles increases the reflectance (Gardner and Sharp, Reference Gardner and Sharp2010). The snow reflectance varies with the snow thickness, density, age, the air temperature, and the grain size. Contaminants such as dust or ash dampen the glacier ice and snow reflectance (Gardner and Sharp, Reference Gardner and Sharp2010; Warren, Reference Warren2019).
The incidence angle of the solar illumination impacts the reflectance of glacier ice, snow, and water. The solar elevation ϕ is the angle between a point on the earth surface and the sun (Fig. 1). The solar zenith angle θ is the angle between the zenith at a given point and the sun:
The lowest solar zenith angle is reached at the summer solstice.
The open water broadband albedo under clear sky increases following a mathematical logistic curve as θ rises. Additionally, at high solar zenith angles, the albedo is negatively related to wind speed (Pegau and Paulson, Reference Pegau and Paulson2001; Huang and others, Reference Huang, Qiao, Chen, Xue and Guo2019). We expect the surface albedo of snow and ice to increase non-linearly towards higher solar zenith angles (Robock, Reference Robock1980; Gardner and Sharp, Reference Gardner and Sharp2010; Whicker and others, Reference Whicker2022), although, surface roughness can decrease the albedo at high solar zenith angles due to shadowing (Gardner and Sharp, Reference Gardner and Sharp2010; Kern, Reference Kern2022).
Solar angle effects on iceberg area retrievals
When retrieving iceberg areas via a reflectance threshold applied to optical data, the threshold choice affects the number of detected small icebergs and the obtained iceberg sizes (Sulak and others, Reference Sulak, Sutherland, Enderlin, Stearns and Hamilton2017; Moyer and others, Reference Moyer, Sutherland, Nienow and Sole2019; Scheick and others, Reference Scheick, Enderlin and Hamilton2019; Rezvanbehbahani and others, Reference Rezvanbehbahani, Stearns, Keramati, Shankar and Van Der Veen2020). Additionally, high solar zenith angles challenge the threshold choice due to increasingly variable reflectance measurements of open water and ice (Moyer and others, Reference Moyer, Sutherland, Nienow and Sole2019; Kern, Reference Kern2022). In addition to the solar zenith angle, the viewing geometry of a passive sensor relative to the target plane influences the measurement (Fig. 1).
To address varying solar angles, Moyer and others (Reference Moyer, Sutherland, Nienow and Sole2019) raised their 0.13 threshold derived at $\theta \sim 47^\circ$![]() to 0.3 in autumn. Rezvanbehbahani and others (Reference Rezvanbehbahani, Stearns, Keramati, Shankar and Van Der Veen2020) limited their study to low solar zenith angles in high summer. Other studies derived iceberg areas over several months without specifically accounting for varying solar zenith angles (Sulak and others, Reference Sulak, Sutherland, Enderlin, Stearns and Hamilton2017; Scheick and others, Reference Scheick, Enderlin and Hamilton2019). It appears unclear how variations in the solar zenith angle affect the accuracy of iceberg areas obtained from optical satellite remote sensing data. Moyer and others (Reference Moyer, Sutherland, Nienow and Sole2019) accounted to some extent for the illumination variation. However, it is uncertain how adapting the threshold affects the iceberg area error. Quantifying this error is important to understand temporal limits for the iceberg area retrieval from optical satellite data, imposed by the solar angles. In this paper we hence approximate the error in iceberg areas retrieved from optical Sentinel-2 NIR data between solar zenith angles of $45^\circ$
to 0.3 in autumn. Rezvanbehbahani and others (Reference Rezvanbehbahani, Stearns, Keramati, Shankar and Van Der Veen2020) limited their study to low solar zenith angles in high summer. Other studies derived iceberg areas over several months without specifically accounting for varying solar zenith angles (Sulak and others, Reference Sulak, Sutherland, Enderlin, Stearns and Hamilton2017; Scheick and others, Reference Scheick, Enderlin and Hamilton2019). It appears unclear how variations in the solar zenith angle affect the accuracy of iceberg areas obtained from optical satellite remote sensing data. Moyer and others (Reference Moyer, Sutherland, Nienow and Sole2019) accounted to some extent for the illumination variation. However, it is uncertain how adapting the threshold affects the iceberg area error. Quantifying this error is important to understand temporal limits for the iceberg area retrieval from optical satellite data, imposed by the solar angles. In this paper we hence approximate the error in iceberg areas retrieved from optical Sentinel-2 NIR data between solar zenith angles of $45^\circ$![]() and $81^\circ$
and $81^\circ$![]() .
.
Study outline
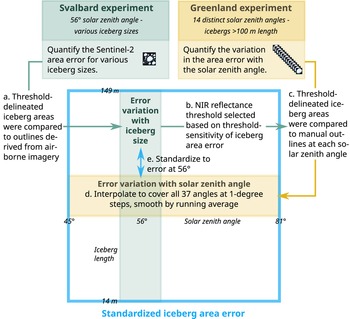
We report on two connected experiments centered around Sentinel-2 data in Svalbard and south-east Greenland. The experiments address iceberg areas retrieved from Sentinel-2 data spanning summer and autumn months, in open water settings.
In the first experiment, we calibrated the Sentinel-2 iceberg NIR reflectance threshold and quantified the iceberg area error at a single solar zenith angle. The calibration was done with reference to iceberg areas derived from optical data acquired during an airborne campaign in Storfjorden, Svalbard, sampled at a 6.25 times finer resolution than the Sentinel-2 satellite data. In the second experiment, we quantified the variation of the iceberg area error with the solar zenith angle. For this purpose, the NIR threshold was applied at 14 solar zenith angles in the Kangerlussuaq Fjord, south-east Greenland. We quantified an iceberg area error at every solar zenith angle with reference to visually delineated large icebergs. The Svalbard experiment calculates an error magnitude over a range of iceberg sizes, whereas the Greenland experiment provides the error variation with the solar zenith angle. Therefore, we standardized the area error from the Greenland experiment to the error obtained in Svalbard experiment. This step approximated the Sentinel-2 iceberg area error for solar zenith angles ranging from $45^\circ$![]() to $81^\circ$
to $81^\circ$![]() .
.
Data
Sentinel-2 data
The Copernicus Sentinel-2 mission consists of two satellites launched in 2015 and 2017. Their Sentinel-2 Multispectral Instrument measures the reflected solar spectral radiances between 443 and 2022 nm central band wavelengths in a 290 km swath (ESA, 2023).
Sentinel-2 level 1C acquisitions with a scene cloud cover below 2% were searched. Acquisitions were dropped when the visually estimated sea ice concentration exceeded roughly 10%. The solar zenith angle θ was calculated in the center of each acquisition using the pysolar software (Stafford, Reference Stafford2023). The processing of the Sentinel-2 to the processing level 1C by ESA has changed over time, resulting in different processing baselines. The data are distributed in digital numbers (DNs) that have to be converted to reflectance data. Products with a processing baseline above 4.0 require subtracting a constant radiometric offset of 1000 from the DNs (ESA, 2024), which was done prior to the conversion to TOA reflectances. The data were then converted to TOA reflectances ρ TOA by applying the coefficient of 10−4 to the DN values. The Sentinel-2 data analyzed in this study are TOA reflectance values ranging from 0 to the saturation value of 1. We did not employ a marine atmospheric correction method to avoid potentially added ambiguities (König and others, Reference König, Hieronymi and Oppelt2019). A cloud probability map was calculated using the s2cloudless algorithm (Skakun and others, Reference Skakun2022), and probabilities above 5% were flagged as clouds. The NIR band (B8), denoted ρ NIR, is measured at a 833 nm wavelength with a 105 nm bandwidth, and sampled at a 10 m spatial resolution (ESA, 2023). We used only ρ NIR as it contains less atmospheric scattering than the other 10 m resolution bands.
Storfjorden, Svalbard
The variation in the iceberg area error with iceberg size was quantified at Storfjorden, East Svalbard (Fig. 2). Negribreen and Sonklarbreen are two tidewater glaciers calving into Storfjorden. The Sentinel-2 tile identifiers covering the Dornier flight paths are 33XWH and 33XXH, acquired approximately at 14:17 pm local time (12:17 UTC) on 21 June 2021 at $\theta \sim 56^\circ$![]() .
.

Figure 2. Maps of the study sites, Storfjorden (a) and Kangerlussuaq Fjord (b). The Storfjorden map shows the Sentinel-2 acquisition on 21 June 2020 at $78.69710^\circ$![]() N, $19.804\, 09^\circ$
N, $19.804\, 09^\circ$![]() E, overlaid by the Dornier tracks. The Sentinel-2 acquisition in the Kangerlussuaq map was acquired on 27 July 2018 at $67.947\, 121\, 30^\circ$
E, overlaid by the Dornier tracks. The Sentinel-2 acquisition in the Kangerlussuaq map was acquired on 27 July 2018 at $67.947\, 121\, 30^\circ$![]() N, $-31.605\, 731\, 89^\circ$
N, $-31.605\, 731\, 89^\circ$![]() W.
W.
Kangerlussuaq Fjord, south-east Greenland
The variation in the iceberg area error with the solar zenith angle was quantified in the Kangerlussuaq Fjord in south-east Greenland in the Sentinel-2 tile 25WER (Fig. 2). The Kangerlussuaq glacier accounts for 5% of the mass balance of the Greenland ice sheet (Enderlin and others, Reference Enderlin2014). We chose this fjord due to a consistent and large iceberg population in open water during summer months. 14 acquisitions were gathered at solar zenith angles between $45^\circ$![]() and $81^\circ$
and $81^\circ$![]() (Table 1).
(Table 1).
Table 1. Sentinel-2 data, Kangerlussuaq fjord, sorted by θ

Optical airborne data, Svalbard
Optical airborne imagery in the visual bands was collected by a PhaseOne IXU-150 camera mounted on a Dornier aircraft. The acquisition was done in the northern part of Storfjorden, Svalbard, on 21 June 2020 starting at 3:20 pm local time (1:20 UTC), about an hour after the Sentinel-2 acquisitions. The data were georeferencd and downsampled to 4 m spatial resolution post flight.
Meteorological reanalysis data
We gathered 2 m air temperature simulations from the Arctic Regional Reanalysis (CARRA) product (Schyberg, Reference Schyberg2020). The data were downloaded from the Copernicus Climate Change Service C3S Climate Data Store (2021). The current version of the CARRA dataset relies on the HARMONIE-AROME cycle 40h1.1, and is vertically forced by the ERA5 dataset (Køltzow and others, Reference Køltzow, Schyberg, Støylen and Yang2022). The spatial resolution of the CARRA dataset is 2.5 km, and simulations are available every three hours. The closest simulations to the Sentinel-2 timestamps were selected.
Methods
In this study we used two connected experiments to quantify the iceberg area error from Sentinel-2 NIR data as a function of the solar zenith angle. The Svalbard experiment determined a NIR reflectance threshold for delineating iceberg areas, and quantified the iceberg area error for icebergs with lengths between 14 and 149 m. The Greenland experiment quantified the variation in the iceberg area error with the solar zenith angle. By standardizing the error variation (Greenland) to the error magnitude and spread (Svalbard), we yielded the standardized iceberg area error between solar zenith angles of $45^\circ$![]() and $81^\circ$
and $81^\circ$![]() . The subsequent section explains the steps leading to the standardized iceberg area error as summarized in Fig. 3.
. The subsequent section explains the steps leading to the standardized iceberg area error as summarized in Fig. 3.

Figure 3. The two connected experiments aimed to derive a standardized iceberg area error for Sentinel-2 data, applicable over a range of iceberg sizes and solar zenith angles. The blue box depicts the limits of the error with respect to the iceberg sizes covered by the Svalbard experiment, and the solar zenith angles covered by the Greenland experiment.
Sentinel-2 iceberg detection
We detected icebergs by testing every pixel in the ρ NIR data against a reflectance threshold (Sulak and others, Reference Sulak, Sutherland, Enderlin, Stearns and Hamilton2017; Scheick and others, Reference Scheick, Enderlin and Hamilton2019; Moyer and others, Reference Moyer, Sutherland, Nienow and Sole2019; Rezvanbehbahani and others, Reference Rezvanbehbahani, Stearns, Keramati, Shankar and Van Der Veen2020). The threshold was varied in the Svalbard experiment; details are described subsequently. The measurements above the threshold were flagged as iceberg pixels. Adjacent pixels are considered to belong to the same iceberg. An iceberg detection is a polygon geometry delineating the connected pixels.
Iceberg area error metrics
Iceberg areas were calculated in m2. However, the square root of the areas (m) is reported in this study when applicable to provide an approximate length scale, referred to as root length. All error metrics were calculated upon the area values. The Dornier iceberg areas are denoted as A DO and the Sentinel-2 iceberg areas as A S2. The relative error RE between reference iceberg areas and the Sentinel-2 iceberg areas was calculated in both experiments. In the Svalbard experiment, the reference is the set of Dornier iceberg areas. In Greenland, the reference is the set of visually delineated icebergs. We derived the relative error RE in percentage:
A positive RE implies an overestimation by Sentinel-2 compared to the reference area.
Iceberg threshold calibration
The Svalbard experiment aimed to quantify an iceberg area error over a range of iceberg sizes (Fig. 3). As part of this experiment a suitable NIR-threshold was chosen based on a sensitivity analysis. The reference icebergs were delineated in higher resolution airborne imagery at a single solar zenith angle. The iceberg area error was calculated by directly comparing the airborne iceberg areas with the iceberg areas derived from the Sentinel-2 data (Fig. 3a). The high resolution of the airborne imagery allows a visual delineation of icebergs in the imagery. To speed up the delineation we applied a rough initial threshold that separates icebergs from open water in the 8-bit imagery with digital numbers between 0 and 255. A threshold of 127.5 (50% of the maximum digital number) was applied to the three bands red, green, and blue to obtain an initial delineation of icebergs in the fjord. This threshold was approximately the center between the low ocean measurements (DN ≤ 100) and the high ice measurements (DN ≥ 150). The rough threshold only yielded an initial delineation of ice in the fjord. We then refined the delineations visually when darker parts of the icebergs had not been captured by the initial threshold. To examine the sensitivity of the area error to the NIR threshold, (Fig. 3b), icebergs were detected and delineated in the Sentinel-2 data at a range of reflectance thresholds between 0.06 and 0.22. These thresholds were applied to the $\rho _{_{NIR}}$![]() reflectance data that were scaled between 0-1. For this direct comparison we had to account for the drift between the data acquisitions. Usually we observed drift distances on a 100 m scale. While the start of the Dornier acquisition was one hour after the Sentinel-2 acquisition, the exact time lag increases along the flight tracks. The matching was done visually, using the Sentinel-2 icebergs that were detected at the lowest threshold. Finally, the iceberg areas of the Sentinel-2 icebergs were compared to the Dornier iceberg areas at each NIR threshold. The threshold with the lowest iceberg area error was chosen and applied in the Greenland experiment (Fig. 3b).
reflectance data that were scaled between 0-1. For this direct comparison we had to account for the drift between the data acquisitions. Usually we observed drift distances on a 100 m scale. While the start of the Dornier acquisition was one hour after the Sentinel-2 acquisition, the exact time lag increases along the flight tracks. The matching was done visually, using the Sentinel-2 icebergs that were detected at the lowest threshold. Finally, the iceberg areas of the Sentinel-2 icebergs were compared to the Dornier iceberg areas at each NIR threshold. The threshold with the lowest iceberg area error was chosen and applied in the Greenland experiment (Fig. 3b).
Iceberg area error by solar zenith angle
The Greenland experiment aimed to quantify an iceberg area error over a range of solar zenith angles (Fig. 3). The objective was to quantify the error in the iceberg area retrieval over multiple iceberg sizes in the Svalbard experiment, whereas the Greenland experiment quantifies the error variation with θ. The underlying issue was that the airborne data did not cover a range of solar zenith angles. Furthermore, visually deriving reliable iceberg outlines directly from the Sentinel-2 data is only possible for large icebergs relative to the Sentinel-2 resolution. Therefore, the Greenland experiment featured large icebergs only, creating a consistent dataset that is comparable over time.
Reference iceberg areas
We visually delineated a total of 378 large and very large icebergs, 27 in each Sentinel-2 acquisition, spanning 14 solar zenith angles in the Kangerlussuaq Fjord. The visually delineated areas were compared to the areas delineated by the NIR reflectance threshold (Fig. 3c). To obtain a consistent dataset, we only delineated icebergs with a root length above 100 m. This strategy was employed for two reasons. First, icebergs of this size can be visually delineated in the Sentinel-2 data because spectrally mixed measurements at the edge constitute a smaller proportion of the entire iceberg area. Second, it was only possible to clearly identify shadows at this large size relative to the 10 m resolution of the Sentinel-2 data. On smaller icebergs the spectral mixing at the edge blurs shadows, impeding a reliable delineation that can be trusted as a reference. The visually derived outlines are assumed to cover the entire icebergs above the waterline. In addition, to examine the reflectance measurements of the iceberg and the surrounding water, a 100 m wide buffered belt was created around each outline, covering the iceberg neighborhood. All ρ NIR measurements were gathered separately within the iceberg outline, and in the neighborhood for statistical analysis.
Standardizing the area error to the Svalbard calibration
The Svalbard experiment quantified the magnitude of the relative area error across iceberg sizes. The Greenland experiment quantified the error variation with the solar zenith angle, but limited to large icebergs. The relative error RE θ was calculated for the iceberg pairs at every solar zenith angle. Constrained by the available cloud-free data (Table 1), the solar zenith angles in our dataset are regularly but not equally spaced. Hence we interpolated the RE θ linearly in $1^\circ$![]() steps between $45^\circ$
steps between $45^\circ$![]() and $81^\circ$
and $81^\circ$![]() :
:
with a and b being the indices of the closest lower and higher θ value pair, respectively. The interpolation function f(θ i) was applied at every θ, yielding an RE θ value in degree-steps between $45^\circ$![]() and $81^\circ$
and $81^\circ$![]() . It can be reasonably assumed that the changes in RE θ with a rising solar zenith angle are gradual. However, despite our endeavor to obtain a consistent and comparable iceberg dataset across solar zenith angles, unreasonable oscillations still appeared in RE θ. To smooth these oscillations, we derived running averages in a window of five degrees centered at a specific θ x:
. It can be reasonably assumed that the changes in RE θ with a rising solar zenith angle are gradual. However, despite our endeavor to obtain a consistent and comparable iceberg dataset across solar zenith angles, unreasonable oscillations still appeared in RE θ. To smooth these oscillations, we derived running averages in a window of five degrees centered at a specific θ x:
producing the smooth error $\widetilde {RE}_{\theta }$![]() in $1^\circ$
in $1^\circ$![]() steps (Fig. 3d). The averaging at the lower ($45^\circ$
steps (Fig. 3d). The averaging at the lower ($45^\circ$![]() , $46^\circ$
, $46^\circ$![]() ) and upper limits ($81^\circ$
) and upper limits ($81^\circ$![]() , $80^\circ$
, $80^\circ$![]() ) lacks lower or upper samples, respectively. Here the running average is based on the three or four available values.
) lacks lower or upper samples, respectively. Here the running average is based on the three or four available values.
We understand the Svalbard RE as the error magnitude at $56^\circ$![]() , whereas the Greenland experiment depicts its variation with the solar zenith angle. Hence, the smooth error was standardized to the mean error $\overline {RE}$
, whereas the Greenland experiment depicts its variation with the solar zenith angle. Hence, the smooth error was standardized to the mean error $\overline {RE}$![]() that was derived in the Svalbard calibration at $56^\circ$
that was derived in the Svalbard calibration at $56^\circ$![]() . We scaled $\widetilde {RE}_{\theta }$
. We scaled $\widetilde {RE}_{\theta }$![]() linearly with reference to $\widetilde {RE}_{\theta _{56}}$
linearly with reference to $\widetilde {RE}_{\theta _{56}}$![]() at $56^\circ$
at $56^\circ$![]() :
:
resulting in the standardized iceberg area error SRE θ (Fig. 3e). The 25th and 75th percentiles were equivalently standardized to the percentiles at the $56^\circ$![]() solar zenith angle. At θ = 56°, the standardized iceberg area error thus has the mean value and the interquartile range obtained at that θ in the Svalbard experiment. The variation with θ stems from the Greenland experiment.
solar zenith angle. At θ = 56°, the standardized iceberg area error thus has the mean value and the interquartile range obtained at that θ in the Svalbard experiment. The variation with θ stems from the Greenland experiment.
Results
We first examine the iceberg threshold calibration in the Svalbard experiment. Next, we analyze the variation of the Sentinel-2 iceberg reflectance measurements with the solar zenith angle observed in the Greenland experiment. Finally, we present the standardized iceberg area error for solar zenith angles between $45^\circ$![]() and $81^\circ$
and $81^\circ$![]() .
.
Iceberg threshold calibration
The lowest relative error magnitude was yielded at a 0.12 ρ NIR detection threshold, suggesting this as the most suitable threshold for the iceberg area retrieval from these data. At this threshold the mean RE is 0.19% ± 15.74%. The MAE is 303.33 m2 ± 306.27 m2, corresponding to about three Sentinel-2 pixels at a 10 m resolution.
The highest positive and negative RE values are observed at the low and high end of the tested threshold range (Fig. 4). Correspondingly, the interquartile range tends to increase below and above the 0.12 threshold, which exhibits the lowest spread among all thresholds (Fig. 4).

Figure 4. The RE by the Sentinel-2 ρ NIR threshold. The green dot marks the lowest error magnitude. The dark shaded area covers the interquartile range. The light shaded area covers the range between the 10th (P10) and the 90th (P90) percentiles.
Area error at the 0.12 reflectance threshold
Here we report results obtained at the 0.12 reflectance threshold. The mean iceberg areas of the matched icebergs are close, but larger differences are seen at the margins of the distribution (Table 2).
Table 2. Iceberg root length (m) statistics Dornier & Sentinel-2

The iceberg area distributions are consequently similar, both following a typical distribution with a higher abundance of small icebergs as compared to large icebergs (Fig. 5).

Figure 5. Area distributions for icebergs sampled in the Dornier data (a), and for the identical icebergs delineated by the reflectance threshold applied to Sentinel-2 NIR data (b).
The Sentinel-2 and Dornier iceberg areas exhibit a very strong linear correlation with Pearson's r-value close to 1 and consistent slope and intercept (Fig. 6). Despite the linear agreement, individual icebergs in Fig. 6 deviate in positive and negative directions. To examine RE variations with the reference iceberg size, the Dornier iceberg samples were grouped into area bins (Fig. 7).

Figure 6. The Sentinel-2 and Dornier iceberg areas at the 0.12 threshold. The root length is provided below the labels on the x-axis.

Figure 7. The RE in Dornier area bins. The dark shaded area covers the interquartile range. The light shaded area covers the P10-P90 range. The root length is provided below the labels on the x-axis.
The standard deviation of the RE in the smallest area bin is roughly 19 times the standard deviation in the largest area bin, and the P10-P90 spread is greater, accordingly. This suggests that the RE is more consistent for larger icebergs while the area of smaller icebergs tends to be more erroneous.
Iceberg area error by solar zenith angle
The mean root length of all reference iceberg areas in the Greenland experiment is 326.94 m ± 26.15 m, ranging from 103.27 m to 712.79 m. These statistics summarize all 378 icebergs present in the Greenland dataset. Keep in mind that only large icebergs were sampled in Greenland to create a consistent and comparable dataset over 14 solar zenith angles. The Greenland experiment aimed to quantify the variation in the iceberg area error with the solar zenith angle. Subsequently, the emphasis is therefore on the relative changes in the iceberg reflectance, and changes in the area error with the solar zenith angle. Finally, the standardized iceberg area error is presented, which contains the error magnitude quantified in the Svalbard experiment, and its variation quantified in the Greenland experiment.
Reflectance measurements
At each solar zenith angle, we obtained two sets of ρ NIR measurements: the icebergs and their neighborhoods. Furthermore, the mean 2 m air temperature was taken from the CARRA dataset as the air temperature may affect the reflectance of snow and ice. The mean 2 m air temperature was 2.04°C with two dates below freezing (Fig. 8).

Figure 8. Iceberg (a) and neighborhood (b) ρ NIR by the solar zenith angle, and the air temperature (c). The dashed lines indicate the mean over all 37 values. The dark shaded areas cover the interquartile ranges. The light shaded areas cover the P10-P90 ranges. Note the distinct scaling on the y-axes of the two top subplots.
Up to a solar zenith angle of $58^\circ$![]() , the mean reflectance centers around the mean over all 37 values. Above $58^\circ$
, the mean reflectance centers around the mean over all 37 values. Above $58^\circ$![]() , it varies below the mean, and reaches a minimum at $70^\circ$
, it varies below the mean, and reaches a minimum at $70^\circ$![]() (Fig. 8). This minimum coincides with a positive spike in the air temperature. Past $70^\circ$
(Fig. 8). This minimum coincides with a positive spike in the air temperature. Past $70^\circ$![]() , the mean iceberg reflectance rises, leveling out at $75^\circ$
, the mean iceberg reflectance rises, leveling out at $75^\circ$![]() (Fig. 8). The single mode seen in the reflectance histograms (Fig. 9) flattens above $64^\circ$
(Fig. 8). The single mode seen in the reflectance histograms (Fig. 9) flattens above $64^\circ$![]() . Correspondingly, the standard deviation rises and the distribution becomes right-skewed (Fig. 10). A cluster of saturated samples develops at the high reflectance end from $67^\circ$
. Correspondingly, the standard deviation rises and the distribution becomes right-skewed (Fig. 10). A cluster of saturated samples develops at the high reflectance end from $67^\circ$![]() . The iceberg reflectance becomes multimodal above $70^\circ$
. The iceberg reflectance becomes multimodal above $70^\circ$![]() with a skewness approaching zero (Fig. 10).
with a skewness approaching zero (Fig. 10).

Figure 9. Iceberg and neighborhood ρ NIR histograms at distinct solar zenith angles. The calibrated threshold is shown for reference.

Figure 10. The standard deviation (a) and the skewness (b) of the iceberg ρ NIR measurements by the solar zenith angle.
Area error
The Greenland experiment calculated the RE θ (Fig. 11), which was standardized to the RE quantified in the Svalbard experiment. The result is the the standardized iceberg area error SRE θ (Fig. 11) describing the magnitude and the variation in the iceberg area error when delineating icebergs by the NIR threshold proposed in this study.

Figure 11. The iceberg area errors by the solar zenith angle. The error regimes are denoted above the x-axis. The dashed line corresponds to the light shaded area. The plot contains the RE θ (grey line) quantified in Greenland, and the standardized iceberg area error SRE θ (blue line) representing the magnitude of the iceberg area error quantified in the Svalbard experiment, and the variation quantified in the Greenland experiment.
We identify three SRE θ regimes. In the first error regime up to $65^\circ$![]() , the mean SRE θ ranges between 5.9% and −5.67%. The first error regime is split into positive mean SRE θ values up to $56^\circ$
, the mean SRE θ ranges between 5.9% and −5.67%. The first error regime is split into positive mean SRE θ values up to $56^\circ$![]() , and negative values up to $65^\circ$
, and negative values up to $65^\circ$![]() . The interquartile spread increases with the solar zenith angle.
. The interquartile spread increases with the solar zenith angle.
In the second error regime from $66^\circ$![]() to $72^\circ$
to $72^\circ$![]() , the mean SRE θ drops to reach its largest negative value at $72^\circ$
, the mean SRE θ drops to reach its largest negative value at $72^\circ$![]() , while the interquartile error spread increases steadily. In the third error regime from $73^\circ$
, while the interquartile error spread increases steadily. In the third error regime from $73^\circ$![]() , the mean SRE θ rises towards 0. The interquartile spread flattens, and the upper SRE θ quartile becomes positive from $76^\circ$
, the mean SRE θ rises towards 0. The interquartile spread flattens, and the upper SRE θ quartile becomes positive from $76^\circ$![]() (Fig. 11).
(Fig. 11).
Discussion
In this paper we approximated the error in the iceberg area retrieval from Sentinel-2 data as a function of iceberg size and the solar zenith angle. We first calibrated the iceberg NIR reflectance threshold based on airborne imagery in Svalbard, and quantified the iceberg area error for iceberg sizes with root lengths ranging from 14 to 149 m. We then quantified an iceberg area error at solar zenith angles between $45^\circ$![]() and $81^\circ$
and $81^\circ$![]() in Greenland, which we finally standardized to the error quantified in the Svalbard experiment.
in Greenland, which we finally standardized to the error quantified in the Svalbard experiment.
Iceberg area error as a function of resolution
The spatial resolution of remote sensing data and the error of iceberg area retrievals are intrinsically connected. We observed, consistent with other studies (Sulak and others, Reference Sulak, Sutherland, Enderlin, Stearns and Hamilton2017; Moyer and others, Reference Moyer, Sutherland, Nienow and Sole2019; Rezvanbehbahani and others, Reference Rezvanbehbahani, Stearns, Keramati, Shankar and Van Der Veen2020), that smaller icebergs exhibit an increased error spread.
The airborne data used to quantify the error magnitude have 6.25 times the resolution of the Sentinel-2 data. Even so, the airborne iceberg areas come with an error. It is reasonable to assume that the increased resolution and the acquisition at the bottom of the atmosphere yield more accurate iceberg areas than the Sentinel-2 retrieval. Figure 12 portrays this difference in resolution by showing the maximum negative and positive RE examples, and a moderate example. It is unclear why some of the measurements in Fig. 12a fall below the threshold, producing a high negative error. A shadow on the iceberg causes the underestimated iceberg area in Fig. 12b. Adjacent pieces of ice might contribute to the overestimated iceberg area in Fig. 12c. Though, these examples also depict that the iceberg delineation in the Dornier imagery is not undisputed. Another layer of higher resolution data or direct measurements would be needed to quantify this error.

Figure 12. Maximum negative iceberg area error (a), a moderate error (b), and the maximum positive iceberg area error (c) obtained in the Svalbard calibration. The icebergs were observed at about $78.589\, 448\, 73^\circ$![]() N, $19.856\, 185\, 13^\circ$
N, $19.856\, 185\, 13^\circ$![]() E with a 722 m drift (a), $78.539\, 973\, 04^\circ$
E with a 722 m drift (a), $78.539\, 973\, 04^\circ$![]() N, $19.529\, 583\, 75^\circ$
N, $19.529\, 583\, 75^\circ$![]() E with a 75 m drift (b), and $78.540\, 720\, 6^\circ$
E with a 75 m drift (b), and $78.540\, 720\, 6^\circ$![]() N, $19.512\, 837\, 0^\circ$
N, $19.512\, 837\, 0^\circ$![]() E with a 164 m drift (c). Note that example (a) was located closer to the end of the flight tracks, resulting in a larger time lag between the Sentinel-2 and the Dornier data acquisition.
E with a 164 m drift (c). Note that example (a) was located closer to the end of the flight tracks, resulting in a larger time lag between the Sentinel-2 and the Dornier data acquisition.
Iceberg area error by solar zenith angle
Our standardized iceberg area error SRE θ roughly agrees with the 4% overestimation Moyer and others (Reference Moyer, Sutherland, Nienow and Sole2019) quantified at a $47^\circ$![]() solar zenith angle. The rough agreement seems to confirm the viability of the SRE θ.
solar zenith angle. The rough agreement seems to confirm the viability of the SRE θ.
Nonetheless, it remains debatable how to meaningfully connect the Svalbard RE to the Greenland RE θ. Optimally, we would derive the Svalbard dataset at a range of solar zenith angles, but that was infeasible. The two connected experiments addressed this issue sub-optimally, with drawbacks.
The iceberg areas covered by the two experiments differ fundamentally. The largest iceberg in the Svalbard calibration has half the root length of the mean root length sampled in Greenland. To discuss this we examined the SRE θ spread. As the solar zenith angle increases the slopes on a roughened surface become divided into sun-facing slopes and opposite slopes. The incidence angle of the solar irradiation is lower for the sun-facing slope than for the opposite slope (Gardner and Sharp, Reference Gardner and Sharp2010). At a different scale than the iceberg roughness, Larue and others (Reference Larue2020) showed that the snow albedo at 1000 nm decreases when increasing the surface roughness. Similarly, Lhermitte and others (Reference Lhermitte, Abermann and Kinnard2014) observed a decrease in the albedo of glacier ice with increased surface roughness. More so, a slope facing away from the sun might not receive direct solar irradiation, i.e. is shadowed, at a sufficiently high solar zenith angle. This explains the increased spread in the iceberg reflectance and consequently in the SRE θ at high solar zenith angles (Figs. 14a, c).
We attribute the spread in the SRE θ at a specific solar zenith angle to variations in the meter-scale surface roughness. The first example iceberg at $81^\circ$![]() (Fig. 13e) seems to exhibit a rougher surface and some shadowing, whereas the second (Fig. 13f) appears smoother and differently oriented. Particularly at these high solar zenith angles, an increased meter-scale surface roughness is likely to cause a higher negative SRE θ. In turn, this variation implies that we succeeded to encompass a variety of surface roughnesses. We propose that this variety at every solar zenith angle is more important than the size diversity with respect to the SRE θ variation. Admittedly, we cannot prove this without doubt. Therefore, we emphasize that the SRE θ is an approximation in the absence of a better error estimate across solar zenith angles.
(Fig. 13e) seems to exhibit a rougher surface and some shadowing, whereas the second (Fig. 13f) appears smoother and differently oriented. Particularly at these high solar zenith angles, an increased meter-scale surface roughness is likely to cause a higher negative SRE θ. In turn, this variation implies that we succeeded to encompass a variety of surface roughnesses. We propose that this variety at every solar zenith angle is more important than the size diversity with respect to the SRE θ variation. Admittedly, we cannot prove this without doubt. Therefore, we emphasize that the SRE θ is an approximation in the absence of a better error estimate across solar zenith angles.

Figure 13. Iceberg examples in the Kangerlussuaq Fjord overlaid by the reference outlines and the detected outlines. The icebergs were observed in the Sentinel-2 tile 25WER acquired at $67.947\, 121\, 30^\circ$![]() N, $-31.605\, 731\, 89^\circ$
N, $-31.605\, 731\, 89^\circ$![]() W. The rising abundance of shadows as θ increases results in underestimated iceberg areas (c, d, e). Depending on the surface topography and orientation, the iceberg area may still be accurate at high solar zenith angles (f), which increases the overall spread in the iceberg area error.
W. The rising abundance of shadows as θ increases results in underestimated iceberg areas (c, d, e). Depending on the surface topography and orientation, the iceberg area may still be accurate at high solar zenith angles (f), which increases the overall spread in the iceberg area error.
Implications for optical iceberg area retrievals
We suggest a solar zenith angle of $65^\circ$![]() as a sensible, yet not strict, limit for the iceberg area retrieval from Sentinel-2 NIR data. This is $5^\circ$
as a sensible, yet not strict, limit for the iceberg area retrieval from Sentinel-2 NIR data. This is $5^\circ$![]() below the application-independent recommendation of the European Space Agency (2019), and consistent with Kern (Reference Kern2022) who observed inconsistent illumination on sea ice already below $65^\circ$
below the application-independent recommendation of the European Space Agency (2019), and consistent with Kern (Reference Kern2022) who observed inconsistent illumination on sea ice already below $65^\circ$![]() . Above $65^\circ$
. Above $65^\circ$![]() the SRE θ implies increasingly underestimated iceberg areas with a widening error spread. These changes correspond to right-skewed iceberg reflectance measurements as the solar zenith angle rises. The observed iceberg reflectance applies independently of the SRE θ. Hence high solar zenith angles challenge the iceberg area retrieval from Sentinel-2 near-infrared data and comparable data irrespective of the algorithm used.
the SRE θ implies increasingly underestimated iceberg areas with a widening error spread. These changes correspond to right-skewed iceberg reflectance measurements as the solar zenith angle rises. The observed iceberg reflectance applies independently of the SRE θ. Hence high solar zenith angles challenge the iceberg area retrieval from Sentinel-2 near-infrared data and comparable data irrespective of the algorithm used.
It is questionable how adjusting the iceberg reflectance threshold can tackle this problem. Moyer and others (Reference Moyer, Sutherland, Nienow and Sole2019) increased the NIR reflectance threshold to 0.3 at a $81^\circ$![]() solar zenith angle. Indeed, our study implies underestimated iceberg areas at high solar zenith angles. Hence, a lower threshold would be more sensible to accommodate shadows on the icebergs, in theory. However, without higher resolution reference data, it is difficult to visually distinguish shadows in the Sentinel-2 data from submerged parts of the iceberg, and from the surrounding water. Making this distinction by visual means was only feasible for the large icebergs sampled in the Greenland experiment (Fig. 14).
solar zenith angle. Indeed, our study implies underestimated iceberg areas at high solar zenith angles. Hence, a lower threshold would be more sensible to accommodate shadows on the icebergs, in theory. However, without higher resolution reference data, it is difficult to visually distinguish shadows in the Sentinel-2 data from submerged parts of the iceberg, and from the surrounding water. Making this distinction by visual means was only feasible for the large icebergs sampled in the Greenland experiment (Fig. 14).

Figure 14. Icebergs at θ = 67° (a, b) on 20 September 2018, and at θ = 81° on 26 October 2020 (c, d) in the Kangerlussuaq Fjord. The iceberg locations are $68.002\, 306^\circ$![]() N, $-31.911\, 890^\circ$
N, $-31.911\, 890^\circ$![]() W (a), $68.002\, 306^\circ$
W (a), $68.002\, 306^\circ$![]() N, $-31.911\, 890^\circ$
N, $-31.911\, 890^\circ$![]() W (b), $67.990\, 706\, 0^\circ$
W (b), $67.990\, 706\, 0^\circ$![]() N, $-31.874\, 126\, 7^\circ$
N, $-31.874\, 126\, 7^\circ$![]() W (c), and $68.409\, 449\, 9^\circ$
W (c), and $68.409\, 449\, 9^\circ$![]() N, $-32.333\, 919\, 4^\circ$
N, $-32.333\, 919\, 4^\circ$![]() W (d). The maps show the segregation into shadows and bright sun-facing slopes. The effect is recognizable on small icebergs (b, d), but the resolution impedes a reliable delineation.
W (d). The maps show the segregation into shadows and bright sun-facing slopes. The effect is recognizable on small icebergs (b, d), but the resolution impedes a reliable delineation.
Ambiguity around suitable iceberg thresholds at high solar zenith angles may arise due to the increased mean iceberg ρ NIR. However, we showed that the spread in the reflectance widens above $75^\circ$![]() . Analyzing the, on average, higher reflectance might suggest raising the threshold, but our experiment implies that this is not a viable solution because it does not accommodate shadows. Moreover, shadows on the icebergs converge with the ocean reflectance, which increases with the solar zenith angle (Pegau and Paulson, Reference Pegau and Paulson2001). This suggests an increased overlap between the distributions, making it difficult to accommodate shadows on the icebergs.
. Analyzing the, on average, higher reflectance might suggest raising the threshold, but our experiment implies that this is not a viable solution because it does not accommodate shadows. Moreover, shadows on the icebergs converge with the ocean reflectance, which increases with the solar zenith angle (Pegau and Paulson, Reference Pegau and Paulson2001). This suggests an increased overlap between the distributions, making it difficult to accommodate shadows on the icebergs.
Still, our study leaves open if a dynamically adjusted threshold could reduce the error margins at low solar zenith angles. Moyer and others (Reference Moyer, Sutherland, Nienow and Sole2019) suggested a slightly higher threshold at $47^\circ$![]() . We explored this briefly, confirming a threshold above (below) 0.12 below (above) $56^\circ$
. We explored this briefly, confirming a threshold above (below) 0.12 below (above) $56^\circ$![]() . However, we doubt that our Greenland dataset facilitates deriving such adjusted thresholds reliably. Instead, we suggest using the SRE θ for potentially correcting iceberg area retrievals. This correction is most viable up to $65^\circ$
. However, we doubt that our Greenland dataset facilitates deriving such adjusted thresholds reliably. Instead, we suggest using the SRE θ for potentially correcting iceberg area retrievals. This correction is most viable up to $65^\circ$![]() due to the consistency in the error.
due to the consistency in the error.
Limits in scope
Detection performance
Our study leaves unclear what the detection performance trade-off is between true positive, false positive, and false negative iceberg detections. Reflectance thresholds primarily confuse icebergs with sea ice floes (Sulak and others, Reference Sulak, Sutherland, Enderlin, Stearns and Hamilton2017; Moyer and others, Reference Moyer, Sutherland, Nienow and Sole2019; Scheick and others, Reference Scheick, Enderlin and Hamilton2019). Thus, the detection performance will largely depend on the setting of the evaluation. Our threshold is not necessarily the best to balance the performance trade-off. A higher threshold likely produces fewer false positive detections (Scheick and others, Reference Scheick, Enderlin and Hamilton2019), in particular with respect to sea ice floes (Moyer and others, Reference Moyer, Sutherland, Nienow and Sole2019). Though, it may also miss more icebergs. We have examined the impact of high solar zenith angles on the iceberg retrieval, but we have not quantified how the solar zenith angle impacts the detection of icebergs. We expect a suitably-trained convolutional neural network to be more skilled in detecting icebergs particularly in complex ice mélange, as Rezvanbehbahani and others (Reference Rezvanbehbahani, Stearns, Keramati, Shankar and Van Der Veen2020) showed for Planet data. Potentially, a similar machine learning algorithm could be trained on Sentinel-2 data. Training data may be generated by applying the NIR reflectance threshold with a subsequent manual filtering of false detections. We recommend covering a variety of solar zenith angles in the training, but limited to a suitable range.
Air temperature
Inherently our study cannot reveal how the area error behaves outside the covered air temperatures. Nearly all data were obtained at positive air temperatures. The drop in the iceberg reflectance on 28 September 2021 coincides with the maximum mean air temperature obtained in the dataset. Still, despite an air temperature slightly above freezing, the RE θ is similar on the 6 October 2021. This is a weak sign that the air temperature might be negligible concerning iceberg areas, at least at the mostly positive temperatures in our study. Indeed, we cannot prove this, and we had limited samples below freezing.
Outlook
The results of the presented study may help limit iceberg studies to suitable solar zenith angles, and correct iceberg area retrievals. This knowledge is valuable for applying the method on a larger spatial and temporal scale. However, other errors are important to take into account when calculating total iceberg areas. In particular, sea ice floes are likely to be wrongly identified as icebergs. Sulak and others (Reference Sulak, Sutherland, Enderlin, Stearns and Hamilton2017) proposed statistically correcting for sea ice, although this requires additional knowledge of the local sea ice proportion. Automatically distinguishing icebergs from sea ice would not only be beneficial for automating the iceberg detection, but also to quantify the composition of ice mélange.
The iceberg calving term accounts for a large amount of the uncertainties in the glacial mass balance in marine-terminating glaciers (Alley and others, Reference Alley2023). Improving and further validating the iceberg area retrieval from satellite data is therefore important, although information on iceberg areas alone is insufficient to quantify the calving volume. We hence emphasize connecting observations of iceberg populations and ice mélange to observed and modeled changes in the glacier termini (Foga and others, Reference Foga, Stearns and Van Der Veen2014; Amaral and others, Reference Amaral, Bartholomaus and Enderlin2020; Wehrlé and others, Reference Wehrlé, Lüthi and Vieli2023) on extended spatial and temporal scales. We suggest utilizing both synthetic aperture radar data and optical data for retrieving iceberg areas.
Conclusions
We approximated the error in iceberg area retrievals from top-of-atmosphere Sentinel-2 near-infrared reflectance data at solar zenith angles between $45^\circ$![]() and $81^\circ$
and $81^\circ$![]() . Our study proposes a Sentinel-2 near-infrared reflectance threshold for detecting and delineating icebergs, and it provides the error in the area retrieval with varying solar zenith angles. We recommend applying the proposed threshold up to a solar zenith angle of $65^\circ$
. Our study proposes a Sentinel-2 near-infrared reflectance threshold for detecting and delineating icebergs, and it provides the error in the area retrieval with varying solar zenith angles. We recommend applying the proposed threshold up to a solar zenith angle of $65^\circ$![]() . Meanwhile, we emphasize general limitations of a constant reflectance threshold, in particular its inability to reliably distinguish icebergs from sea ice. To conclude:
. Meanwhile, we emphasize general limitations of a constant reflectance threshold, in particular its inability to reliably distinguish icebergs from sea ice. To conclude:
1. The iceberg area retrieval is consistent up to a solar zenith angle of $65^\circ$
 .
.2. At a solar zenith angle of $56^\circ$
 , the NIR reflectance threshold of 0.12 yields the most accurate iceberg areas.
, the NIR reflectance threshold of 0.12 yields the most accurate iceberg areas.3. Iceberg areas sizes are increasingly underestimated with a rising solar zenith angle, and the error spread increases.
4. Shadows formed by the meter-scale iceberg surface roughness and its orientation are the main error sources at high solar zenith angles.
Data
The code written to conduct this study is available on GitHub: https://github.com/hfisser/S2-iceberg-areas. Data can be requested from the corresponding author.
Acknowledgements
The authors wish to acknowledge the support from the Research Council of Norway through the RareIce project (326834) and the support from all RareIce partners.
We are thankful for the valuable data provided by the Copernicus program of the European Commission, and by the Svalbard Integrated Arctic Earth Observing System (SIOS). This study contains modified Copernicus Sentinel data (2016-2021) and modified Copernicus Climate Change Service information (2016-2021). This study contains airborne data retrieved through SIOS (2020).
Author contributions
HF performed all calculations and wrote most of the paper, HF processed and analyzed the data, HF, APD, and KVH designed the research, and contributed to writing and editing the paper.