Introduction
During the German Antarctic Expedition in 1980–81 a research programme was begun for the investigation of the time-dependent vertical deformation of the upper layers of ice shelves. This depends on the rheological behaviour of the snow or firn. The equipment for long-term observation was installed during the construction of Georg von Neumayer station (70°37´S, 8°22´W) on Ekstrôm Ice Shelf.
Using an extensiometer the vertical deformation of these upper layers caused by snow accumulation and/or the dead weight of structures will be observed during the next decade. The measuring points are located underneath and outside the buildings.
The snow and firn layers under consideration are now 5 to 10 m deep, and after 10 a they may lie approximately 12 to 20 m deep, depending on snow accumulation and drift. During the season 1981-82 the installation of measuring devices is planned at 30 to 50 m depths in order to study ice layers.
The test methods and the measuring device are described. First settlement data are analysed and compared with deformations computed under the assumption of constant compressive viscosity.
1. Density-Depth Relationship
The general increase of snow density with depth results from compression of snow by the load of the annual accumulation. This density increase will occur also from other loads such as structures. Snow density is an important factor governing the mechanical behaviour of snow, firn, and ice including the com-pressive viscosity n1.
During the 1980-81 expedition cores were taken from bore holes down to 12 m on the Ekström Ice Shelf. The density of the snow samples to 10 m depth is shown in Figure 1 as depth-density curve b.
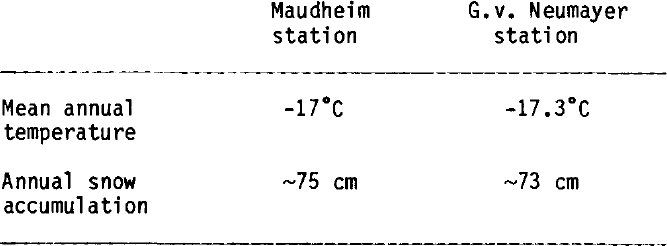
In addition density values from Maudheim station (71°03´S, 10°55´W) are plotted in Figure 1, curve a (Mellor 1961). The reasonably good fit of both curves may be caused by similar climatic conditions at both places as far as the mean annual temperature and the annual snow accumulation is concerned. The values in Table I are taken from Reference Bader and KuroiwaMellor (1961) and Reference Reinwarth, Rauert, Stichler and MoserReinwarth and others (1982).

Fig.1 Depth-density curves: (a) Maudheim station, (b) Georg von Neumayer station, (c) stratigraphy at Georg von Neumayer station.
Table 1 Mean Annual Temperature and Annual Snow Accumulation at Maudheim Station and Georg Von Neumayer Station
Besides the general increase of density with depth considerable discontinuities were found in the snow stratigraphy (Reinwarth and others 1982).
2. Test Method
The measuring device specially developed for this in situ investigation of vertical deformation is shown schematically in Figure 2(a) and after installation in Figure 2(b). Essential parts of the extens-iometer are the base plug at the bottom of the bore hole and the upper metal plate which is placed on the snow surface during installation. After drilling the bore hole to the desired depth the base plug is placed at the bottom of the bore hole and heated electrically. As the firn melts the plug sinks down for about 20 cm. After the electric heating source is switched off the plug becomes frozen into the surrounding snow. The bore hole itself is lined with tubes of different diameter which act as telescope casings to permit free vertical movement of the snow and firn without hindrance. The casings are attached to the upper metal plate which serves as the boundary of the firn layer under consideration; the lower boundary is marked by the base plug.

Fig.2(a). Schematic drawing of the measuring device for long-term observations of vertical deformation.

Fig.2(b). Measuring device after installation.
Additional tubes are fixed to the upper side of the metal plate. These tubes will be extended in succeeding years to the new snow surface providing access for measuring to the base plug and to the metal plate. The distance from the base plug and the metal plate, respectively, to the top edge of the extension tubes will be measured by a calibrated tape which has a heavy metal ball on the lower end, which rests on the knife-edge support of the base plug. The tension of the measuring tape is controlled by a spring balance at its upper end.
These measuring devices have been installed at ten sites (P1 to P10), and in four reference points (Fl to F4, see Fig 3). The sites are located partly underneath and partly outside the buildings. The reference points, however, are positioned at a distance of 100 m from the station to ensure that the buildings do not exert any influence on the measurements.

Fig.3. Position of measuring and reference points near Georg von Neumayer station.
The measurement of the vertical deformation of two snow/firn layers of different thicknesses is shown in Figure 4. Loads due to snow accumulation or to structure dead-weights generate time-dependent vertical deformation by compaction of the snow. Immediately after the installation and after a certain time interval the distance between the base plug and the upper metal plate is measured, and the difference Ah of the two readings can be taken as the vertical deformation of one snow layer (Δh = h-h*).

Fig.4. Description of deformation measurements.
This value Δh represents the deformation of the whole snow and firn layer between the base plug and the metal plate. The time-dependent variation of Ah is caused by the loads and the rheological behaviour of the material. In this way the Ah data incorporate all processes that occur in situ, but cannot be simulated in laboratory tests. Additionally the station buildings act as loads one order of magnitude greater than the annual accumulation, so that densification is faster than it would be with normal snow accumulation outside the station, for example at the reference points.
Every year at least these measurements will be repeated. From the measured deformation the change of the mean density of the snow/firn layer under consideration and the rheological properties of the upper ice shelf layers can be calculated.
To measure settling rates from the station build-ings during the winter period, when the reference points outside the station cannot be reached, measuring scales are installed in ten cross-sections on the side walls of the main tubes.
3. Formulation of the Deformation Behaviour
When considering the time-dependent compression behaviour of ice-shelf ice, the Burgers model (Fig.5), which is a combination of a Maxwell unit and a Voigt unit can be used (Bader 1962, Mellor 1975). The deformation derived from this model is

where σ is the load, E1 the spring constant of the Maxwell model approximately equal to Young´s modulus of the snow, E2 the spring constant of the Voigt unit, n 1 the viscosity, t the time, and the reference time. In this equation, part 1 is related to the deformation of the Maxwell unit and part 2 to the relaxation deformation of the Voigt unit. This later part can be neglected with regard to long periods (Bader 1962). It is assumed also that the instantaneous elastic deformation ε = σ/E1 can be neglected because of the magnitude of the modulus of elasticity E1 appropriate to the snow density of the upper zone of the Ekstrôm Ice Shelf (Mellor 1975, Jessberger and Dorr 1981). For the given conditions (small load, high modulus of elasticity, sufficient loading time) only the viscous deformation ε = σ.t/n1 remains and this depends linearly on the time and inversely on the compressive viscosity n1.

Fig.5. Burgers model.
Ramseier and Pavlak (1964) reported experimental results for the compressive viscosity (Fig 6), which, according to Haefeli and Brandenberger (1968), can also be calculated for a distinct location from the depth-density relation. Appropriate viscosity values calculated by the authors for Georg von Neumayer station are plotted in Figure 6. These data compare reasonably well with the n1-ρ relation for Byrd station.

Fig.6. Compressive viscosity vs density (Ramseier and Pavlak 1964).
4. Calculated and Measured Vertical Deformations
The following discussion refers to the east tube of the station, which has a ground area of about 50 × 8 m and a foundation pressure of roughly 50 kPa. Because of the viscous properties of snow and firn the vertical deformation of the layers underneath the tube will increase with time. During the Antarctic winter and summer of 1981–82 this behaviour was determined by measuring the differential settlement of the tube.
The centre point M of the ground area in Figure 7(a) corresponds to cross-section VIII in Figure 3, the outer points A and A' correspond to cross-sections VI and X respectively. In Figure 7(b) the measured differences in the settlement of the tube are shown. The open and full circles belong to the differential settlement (sM - sA) and (sM - sA') respectively.

Fig.7 (a)Generalized settlement curve. (b)Time-dependent differential settlements.
The calculation of the settlement of the tube at point M and A has been performed in the following way (Fig 8). The stress distribution versus depth was calculated according to Boussinesque down to the depth z = 20 m. The viscous strain εi of any chosen layer is calculated to be
where σzi is the vertical stress in the middle of layer i, t the time, and n1(i) the compressive viscosity depending on density (see Fig 6). The total settling of each point is
The different vertical stress distribution underneath M and A(A'), leads to the differential settlings
given in the line of Figure 7(b).

Fig.8. Process of calculation of settlements under loads on a viscous medium.
It should be mentioned that the vertical deformation of the firn causes an increase of density followed by an increase in viscosity. However, during the period of observation, so far, this change is not yet significant so that the assumption that the viscosity has been constant should be acceptable. The differences between the calculated and the measured As values are caused by the assumption made for the calculation and also by the procedure of the station construction. The comparison between calculated results and these first measurements is encouraging. These vertical deformation measurements, therefore, together with vertical magnetic probe extensiometer readings and inclinometer readings in special grooved deformable casings will be included in long-term observations made at the station.
Acknowledgements
The financial support of the Bundesminister für Forschung und Technologie (BMFT) and the Deutsche Forschungsgemeinschaft (DFG) as well as the cooperation of N Diekmann, P Jordan, and 0 Bangel are gratefully acknowledged.












