The mass balance of a dry snow surface during a snowstorm

Abstract

This paper focuses on the surface mass balance of a horizontally homogeneous snowfield, with emphasis on the effects of snowdrift sublimation. A one-dimensional model of the atmospheric boundary layer that includes snowdrift physics and thermodynamics is used. In sufficiently strong winds, snow particles are eroded from the surface. Once airborne, they are susceptible to sublimation. Averaged over longer time periods, the net erosive flux equals sublimation of snowdrift. However, model results show that there is no such balance in the course of a snowstorm event. They also indicate that snowdrift sublimation tends to enhance net erosion, but the increase occurs more slowly than the mass transfer by snowdrift sublimation, and the maximum is smaller. This difference in temporal behaviour influences the average erosion rate owing to non-linear interactions between snowdrift sublimation, drift density and erosion. Since the increase in relative humidity due to snowdrift diminishes surface sublimation, the average change in total ablation induced by snowdrift sublimation remains small. Observations made during snowdrift episodes in Antarctica agree qualitatively with some of the model results.

1. Introduction

Over an irregular surface topography covered by snow, erosion and deposition of wind-transported snow usually contribute to a complex spatial pattern of net accumulation (e.g. Liston and Sturm, 1998; Gauer, 2001). This is due to horizontal divergences and convergences of the amount of snow transported by the wind, which depend chiefly on the surface wind field and snow surface conditions. However, even in the absence of spatial variations in wind speed, interactions between the various snowdrift-related processes (erosion, deposition, vertical transports, sublimation) can complicate the effects of snowdrift on the surface mass balance (Bintanja, 2001c). In this paper, we will investigate such interactions and discuss their effect on the instantaneous and the average mass balance. We will only address the simplest possible case (horizontal homogeneous conditions) by using a one-dimensional (vertical) model of the atmospheric boundary layer that includes snowdrift.

Averaged over a large area and period, the net mass loss of a dry snow surface is due only to sublimation of drifting snow and to surface sublimation (Bintanja, 2001a). These two fluxes of latent heat represent the total surface-to-atmosphere moisture transport. Before snowdrift sublimation can take place, however, snow particles must have been eroded from the surface. Hence, the instantaneous (or local) ablation rate is strictly the sum of net erosion and surface sublimation. Once snowdrift sublimation takes place, the mass of the suspended load is depleted (particles become smaller), which favours a net upward transport of particles. In steady-state snowdrift, there is a balance between the vertically integrated snowdrift sublimation rate and the net upward transport of snow particles at the surface.

Since snowdrift sublimation is such an efficient mechanism (the exposed surface area of all suspended particles is very large) it quickly saturates the lowest atmospheric layers (Déry and others, 1998; Mann and others, 2000; Bintanja, 2001c), causing surface and snowdrift sublimation rates to decline. This constitutes a negative feedback that effectively limits the surface-to-atmosphere moisture flux during snow-drifting conditions. In this paper, we will show that quantities such as net instantaneous ablation, average ablation and the total moisture flux to the atmosphere during snowdrift episodes depend on interactions between snowdrift sublimation, drift density and net erosion, even in horizontally homogeneous conditions.

2. Method

Wind transport of snow is a highly non-linear process. It is non-linearly related to wind speed, snow age, snow crystal shape and snow temperature. In fully developed snowdrift, particles are either in saltation (periodic contact with the surface) or in suspension (free-floating) (creep is ignored here). Particles in suspension migrate horizontally at the velocity of the wind (Schmidt, 1986). We assume horizontal homogeneous conditions, so that the horizontal transport of snow does not vary spatially. The flux of snow into a given volume (S_in) equals that leaving the volume (S_out) (see Fig. 1). Erosion (E) and deposition (D) of snow determine the amount of airborne mass (precipitation is ignored), where the net erosion (NE) equals

Fig. 1. Schematic representation of the simulated fluxes of snow and moisture.

(1)

Net erosion and surface sublimation (LH^s, representing the sublimation of immobile particles at the bed) determine the ablation rate (A):

(2)

Evidently, a positive value of A indicates that the surface loses mass to the atmosphere. The net flux of moisture from the surface to the atmosphere (LHA) equals the sum of surface (LHs) and snowdrift (LHd) sublimation:

(3)

Averaged over a sufficiently long period, net erosion equals snowdrift sublimation, and ablation equals total sublimation. We will employ the one-dimensional model SNOWSTORM to simulate the time-dependent behaviour of the various fluxes. Hence, it is assumed that fields of temperature, humidity and suspended particles are horizontally homogeneous, and that the topography is flat compared to the saturation length scale of snowdrift (so that fully developed snowdrift conditions exist). A detailed description of this model, including details of the snowdrift sublimation calculations, can be found in Bintanja 2000, 2001b). In brief, for a given wind-speed profile the model simulates the vertical distribution of spherical snow particles in 48 size classes based on turbulent diffusion, gravitational settling and snowdrift sublimation. The model numerically solves the surface-layer balance equations for momentum, heat, moisture and suspended particles. Snowdrift sublimation is a function of wind speed (ventilation rate), relative humidity of the air, particle radius and air temperature (see Dover, 1993), and causes a steady reduction in the size of the particles. The ventilation rate of each particle depends on its terminal fall velocity (i.e. weight) and on the turbulent intensity of the relative (air-particle) velocity fluctuations (larger for big particles). Snowdrift sublimation causes a cooling and a moisture input of the surface layer. The total snowdrift sublimation rate (LHd) is obtained by integrating over the particle spectrum and over the height of the suspension layer (from the saltation–suspension interface up to 100m). Snowdrift sublimation rates calculated with SNOWSTORM agree well with those derived from other snowdrift models (Xiao and others, 2000). Surface sublimation is included as the normal eddy surface-layer latent-heat flux, and as such depends on wind speed and the specific humidity gradient at the lower boundary.

In the saltation layer, sublimation of snowdrift can be neglected if it is assumed that the saltation layer becomes saturated very quickly after the onset of snowdrift (which is probably a good assumption). Since snowdrift transport is dominated by suspension (Pomeroy and Male, 1992), we will define the erosion and deposition rates at the bottom of the suspension layer (the suspension–saltation interface, h) in terms of local upward diffusion and gravitational settling:

(4)

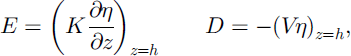
where K is the turbulent eddy exchange coefficient of suspended particles, η is the drift density (kgm^–3) of suspended snow particles and V is the radius-dependent terminal fall velocity of the particles. We use the empirical relation of Pomeroy and Gray (1990) to estimate the saltation drift density as a function of wind speed. Particles that remain in the saltation layer before being deposited do not contribute to net erosion nor have they any effect on sublimation. Saltation particles serve as a source for the suspended load. For the purpose of this paper, this seems to be a feasible approach. Note that the processes involved in particle erosion in the saltation layer are notoriously complicated (Ungar and Haff, 1987; Pomeroy and Gray, 1990); they involve particle ejection through rebounding particles and dissipation of turbulent kinetic energy of the airflow, among others.

We have forced the model with a Gaussian-shaped storm (Fig. 2a), which mimics the passing of a large-scale weather system such as a synoptic pressure gradient. When the friction velocity is greater than the threshold for snowdrift initiation (taken here as 0.25 ms^–1, equivalent to a 10 m wind speed of 7.2 ms^–1which is typical for Antarctic snow surfaces (e.g. Mann and others, 2000)), snowdrift will occur. Our modelled snowstorm lasts for 2 hours 45 min, after which the model run continues for another 3 hours to enable airborne snowdrift particles to settle. Our initial air and snow temperature is –10°C everywhere (both decrease slightly in the course of the model run due to the cooling effect of snowdrift sublimation), while initial relative humidity (with respect to ice) decreases from 100% at the surface to 70% at 100 m.This situation is typical for Antarctic summer.

Fig. 2. Simulated variations in (A) wind speed, (B) net erosion, (C) sublimation rates, (D) relative humidity at two heights, and (E) relative height of the snow surface during a model storm that lasted 2.75 hours (the hatched area indicates when winds were stronger than the threshold wind speed of 7.2 m s^–1 for snowdrift) and the period thereafter. Note that a latent-heat flux of 32.8Wm^–2 represents a sublimation rate of 1mm w.e. d ^–1. Snow density has been set at 400 kgm^–3. was ignored. However, the interaction with the slow erosion/deposition process and especially the opposing change of surface sublimation shade this simple conclusion. The average difference in moisture flux (LHA) is also small, even though there is a sharp increase at the beginning of the storm due to snowdrift sublimation.

3. Model Results

The net erosion rate for the model storm over flat terrain is depicted in Figure 2b. Clearly, net erosion occurs for increasing winds, whereas deposition takes over when winds diminish. Small snow particles with low fall velocities can be swept up to substantial heights. Therefore they can remain in the air long after the storm has ceased, as indicated by the ongoing deposition after the storm has faded. Also note that NE peaks just before the winds reach their maximum.This is because erosion and deposition are slightly out of phase (deposition always trails erosion in its aim to balance erosion to establish NE = 0).

Surface and snowdrift sublimation rates are depicted in Figure 2c. Surface sublimation is small and vanishes quickly once snowdrifting starts.This is because snowdrift sublimation very efficiently puts water vapour into the lowest atmospheric layers (where most particles are), which quickly leads to saturation of the air (Fig. 2d) and to a zero vertical gradient in specific humidity at the surface (which governs the surface sublimation rate). Hence, snowdrift sublimation effectively shuts off surface sublimation. (Incidentally, surface sublimation does not recover after the storm, as there are no mechanisms that can put moisture back in; model runs (Table 1) show that this can be overcome by incorporating advection of relatively dry air, but these results were not qualitatively different from those shown in Figure 2. Snowdrift sublimation and especially surface sublimation increase because the air remains undersaturated, and the total moisture flux increases, as well as net erosion.) Snowdrift sublimation also diminishes for the same reason, as its value is proportional to the undersaturation of the air (e.g. Thorpe and Mason, 1966). This is why the maximum snowdrift sublimation precedes the maximum wind speed. In the fully developed storm, the air close to the surface becomes saturated and no snowdrift can sublime there. Note that the maximum value of LHd is roughly 25% of net erosion at that time.

Table 1. Summary of results of sensitivity tests. Values of 10 m wind speed (WSP), the maximum value of net erosion (NE (max)), and mean values of snowdrift sublimation, surface sublimation and the net moisture flux are given

Total sublimation (i.e. the moisture flux from the surface to the atmosphere) is dominated by snowdrift sublimation (Bintanja, 2001b). Net erosion equals snowdrift sublimation when integrated over the entire period; suspended particles either sublime or fall back to the surface. The ablation rate (as measured by a device measuring the height of the snow surface, for instance (e.g. Reijmer and Oerlemans, 2002)) is governed by net erosion. The simulated height of the surface is depicted in Figure 2e. Initially, erosion eats away the top layers of snow, but deposition replenishes a large portion of the snow when the winds drop. The difference between end and begin level represents the mass lost by sublimation.

To elucidate the effects of snowdrift sublimation, we have repeated the model run but with snowdrift sublimation set equal to zero at all times. The results are shown in Figure 3. As expected, net erosion is smallest when snowdrift sublimation is suppressed. This is due mainly to changes in deposition rate: in case of non-zero LHd, snowdrift sublimation deprives the suspended load of mass that would otherwise be redeposited at the surface. Moreover, snowdrift sublimation acts to decrease the size of the suspended particles. As a result, particle fall velocities become smaller and particles can stay in the air for longer.

Fig. 3. Difference (the case with snowdrift sublimation minus the case without it) in net erosion, surface and snowdrift sublimation rates, ablation rate and total moisture flux over the modelled period. The hatched area indicates when winds were stronger that the threshold wind speed of 7.2 m s–1 for snowdrift.

The difference in net erosion is maximum at the peak of the storm and then falls off slowly (Fig. 3). More interesting, however, is that snowdrift sublimation (LHd) is much larger than the difference in net erosion. This means that while snowdrift sublimation acts to increase net erosion, the latter is unable to keep up with it (if they were equal, the extra sublimation would be instantenously translated into extra erosion). Hence, the “occurrence” of snowdrift sublimation leads to an increase in moisture flux to the atmosphere that is much stronger (weaker) at the beginning (end) of the storm (averaged over the entire event they are the same). This is due to the efficiency of the snowdrift sublimation process. Importantly, the difference in response time affects the mean value of net erosion (and LHd): if net erosion reacted as efficiently as snowdrift sublimation then the average value of sublimation and net erosion would be larger.

Also LHs changes under the influence of snowdrift sublimation, as can be seen in Figure 3. In the absence of snowdrift sublimation, the air near the surface remains undersaturated, and surface sublimation (being proportional to the wind speed) increases to about 50Wm^–2 at the peak of the storm. This indicates that snowdrift sublimation significantly diminishes LHs. In fact, the decrease in LHs is of the same order of magnitude as the increase in net erosion, implying that the change in ablation associated with the “occurrence” of snowdrift sublimation remains small. This is a somewhat surprising result, as one might have expected ablation to decrease if snowdrift sublimation

Model runs with other types of wind forcing (form, strength, duration) show that the results depicted here are robust. Table 1 depicts results for different wind strength. It is seen that mean snowdrift sublimation increases with wind speed (the effect of more particles is more important than the humidity feedback), whereas mean surface sublimation decreases (because of the increase in humidity). The total moisture flux increases (slightly) with wind speed, as does peak erosion.

4. Comparison with Observations

Calculations of snowdrift, in particular of snowdrift sublimation, are hard to verify with data (Bintanja, 2001c). This is because, even today, measuring snowdrift characteristics and latent-heat fluxes is still an arduous undertaking in the atmospheric conditions typical of snowstorms. As a result, few reliable datasets exist to date.

For the purpose of this paper, we will try to verify our calculations in another (more indirect and qualitative) way by using appropriate ablation measurements and compare these with Figure 2e. Since 1996, the Institute for Marine and Atmospheric Research Utrecht (IMAU) has operated several automatic weather stations (AWSs) in Dronning Maud Land, Antarctica (Reijmer and Oerlemans, 2002). As well as the standard meteorological quantities, these AWSs measure the height of the snow surface, and hence the local mass balance (if compression of snow is ignored). One of these AWSs (74°29′ S, 11°310W; 1160ma.s.l.; slope 15 m km^–1) is located at about 16 km from the Swedish research station Svea on a gently sloping but otherwise flat snow surface. A detailed meteorological experiment in austral summer 1997/98 demonstrated that snowdrift characteristics at this location agree with those observed at other undisturbed locations with a sufficiently long fetch (Bintanja, 2001a).

We selected one of many possible examples. Figure 4 shows measured wind speed as well as the relative change in surface height during a 5 day period in August 1999. In the night of 5 August the wind picks up and snowdrifting starts. The snowstorm continues for about 3 days and exhibits two distinct peaks in wind speed. During the first part of the storm, the surface height drops by about 10 cm. In analogy with Figure 2e, this decrease can be attributed to wind erosion. On the morning of 7 August the wind speed falls. As a result, net erosion halts. Thereafter the surface height increases (due to deposition), only interrupted briefly by another erosion episode that follows from the second wind-speed maximum. Hence, the analogy with our model snowstorm is quite obvious (even though the magnitude of the changes in surface height is larger than in our model study). At the end of the storm, the overall surface lowering amounted to 5 cm of snow. Unfortunately, we cannot verify this number in a quantitative sense.

Fig. 4. Observed height of the snow surface (measured by a sonic ranger) (A) and observed wind speed (B) for a 5 day period in August 1999 (temperatures were –15 to –25°C and relative humidity was about 80%). The measurements were taken by an AWS near Swedish station Svea (74°29′ S, 11°310W; 1160 m a.s.l.), Dronning Maud Land, Antarctica. The sampling interval was1 hour. The snow-height data were smoothed using a nine-point running mean. The hatched area denotes the approximate period when winds were stronger than the threshold for snowdrift.

The AWS dataset contains many cases that match our model snowstorm in the sense sketched above. This, and the fact that observed moisture fluxes and simulated sublimation rates at the same location (albeit in another period) agreed reasonably well (Bintanja, 2001c), leads us to believe that the simulated temporal variations in erosion, sublimation and ablation are realistic.

5. Conclusions

In this paper, we have simulated the mass balance and the associated surface-to-air moisture flux of a flat snowfield during a snowstorm (in the absence of horizontally changing snow-transport fluxes). A one-dimensional model of the atmospheric boundary layer including snowdrift physics and thermodynamics was used. Model runs reveal that net erosion (erosion minus deposition) dominates the ablation rate. Part of the snow that is eroded from the surface and becomes suspended in the air is sublimed (snowdrift sublimation), which significantly enhances the moisture content of the air. Once the air becomes saturated, snowdrift and surface sublimation diminish.

The effects of snowdrift sublimation on the ablation rate have been investigated. It is found that snowdrift sublimation acts to increase net erosion, but changes in net erosion are relatively slow compared to the efficient snowdrift sublimation process (averaged over a long period, snowdrift sublimation equals net erosion). Snowdrift sublimation diminishes surface sublimation, a decrease that is about as large as the increase in net erosion. As a result, the net effect of snowdrift sublimation on ablation is small. Observed changes in surface height during a snowstorm exhibited temporal variations similar to those simulated, but with larger amplitude.

The mean value of the total surface-to-atmosphere moisture flux (the sum of surface and snowdrift sublimation) does not depend much on whether or not snowdrift sublimation is taken into account. The lesson of this study may be that (a) instantaneous values of net erosion need not equal snowdrift sublimation, and (b) the total moisture flux need not equal surface ablation. These inequalities can be attributed to differences in the physical nature of the mechanisms involved, and as such affect the mean values of erosion, sublimation and ablation.