Introduction
In the European Alps and most other areas of the world the retreat of glaciers is a widely observed fact. The most important climate-change effect on water availability is a change in the timing of streamflow throughout the year (Reference ArnellArnell, 1999), considering that a major proportion of annual streamflow is formed by snowmelt in spring. Furthermore, valley glaciers represent a storage of water. The impact of glacier retreat on water resources is due not only to a smaller storage in the form of ice with increasing melt, but also to the overall decrease in altitude in a catchment. The decrease in altitude leads to higher temperatures and enhances the decrease in the snow to rain ratio. This has implications for the timing of the streamflow, with a shift from spring snowmelt to summer runoff (Reference ArnellArnell, 1999). Ice melt is therefore expected to be enhanced due to earlier snow depletion.
In this paper, ice volume loss has been estimated using DEMs from different time periods. The estimated ice-volume loss and the estimated precipitation from measurements are in good agreement with runoff measurements. An energy-balance model (Snow Distributed Energy balance Model, SnowDEM) was run, with and without a gravitational mass transport and deposition (MTD) routine, for the period 2005/06. The model run, which does not include mass transport, overestimates the water availability in the basin throughout the year by about 40% due to overestimated snow and ice melt. However, the model run in which SnowDEM was coupled with the MTD produced a result closer to the measured runoff. This result leads us to conclude that the distribution of snow is not only important for the correct shape of the hydrograph and the water availability throughout the season, but also for the correct estimation of the runoff and the total water availability.
Methods
The field area
Haut Glacier d’Arolla is a small north-facing temperate valley glacier located in southwest Switzerland on the main Alpine divide. It has been the subject of ongoing research in glacier mass and energy balance, hydrology, geochemistry and ice dynamics since the early 1990s (see, e.g., Reference SharpSharp and others, 1993; Reference Arnold, Willis, Sharp, Richards and LawsonArnold and others, 1996; Reference Hubbard, Blatter, Nienow, Mair and HubbardHubbard and others, 1998; Reference Brock, Willis, Sharp and ArnoldBrock and others, 2000; Reference Willis, N.S. and B.W.Willis and others, 2002; Reference Strasser, Corripio, Pellicciotti, Burlando, Brock and FunkStrasser and others, 2004; Reference ArnoldArnold, 2005; Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others, 2005). The catchment area is approximately 13 km2, with a glaciated area of about 5.3 km2 and an elevation range 2500–3800ma.s.l. (Fig. 1). Haut Glacier d’Arolla, the largest glacier in the area, is 4.4 km2 in area and about 4 km long. It has been retreating since the second half of the 20th century (Reference OerlemansOerlemans and others, 1998). Over the last decade, the equilibrium-line altitude has been well above 2800ma.s.l. (Reference OerlemansOerlemans and others, 1998), leading to a strong negative mass balance, with about 2.5–3ma − 1 of surface ice ablation across the lower tongue and more than 100 m of retreat since 1989 (Reference Hubbard, Blatter, Nienow, Mair and HubbardHubbard and others, 1998). These values have increased during the last 6 years of our measurements.

Fig. 1. Digital map of the Haut Glacier d’Arolla basin. Blue indicates the glaciated area (5.3km2), red stars represent the locations of three automatic weather stations, white star is the location of an automatic camera and yellow circles depict the locations of accumulation/ablation stakes. The inset shows a map of Switzerland with the location of Haut Glacier d’Arolla.
Meteorological and glaciological measurements
The meteorological measurements in the catchment are made at one permanent automatic weather station (AWS) (T1) in the proglacial area at 2500ma.s.l., approximately 1 km distance from the glacier snout, and one permanent AWS (T2) in the non-glaciated part of the upper basin at 3000 ma.s.l., approximately 0.5 km from the glacier margin. Both of these stations are outside the glacier boundary layer. The lower station (T1) is influenced by katabatic winds and therefore records colder temperatures than it would in the absence of a glacier. The upper station (T2) records higher than expected temperatures, being located at a spot in a topographic bowl that warms up more than the rest of the catchment. Both stations measure shortwave incoming and outgoing radiation, longwave incoming and outgoing radiation, air temperature, relative humidity, wind speed and direction and precipitation. Snow height is only measured at T2 with an ultrasonic depth gauge. Another station (AWS glacier) is located on the glacier at about 2800ma.s.l., and is used for validation of the model. Figure 1 shows the location of the automatic weather stations and ablation/accumulation stakes. AWS glacier is equipped similarly to T1 and T2, but lacks the precipitation gauge.
Hourly discharge has been recorded for more than 30 years at a location about 1 km fromthe present glacier snout (100m from T1) by the hydroelectric company Grande Dixence, using a pressure transducer in an artificial channel of known dimensions. The accuracy is given as 10%.
Direct measurements of snow-depth distribution over the glacier were carried out in May 2006. These surveys also included measurements of snow density in snow pits. The snow-depth distribution was measured with a graduated metal pole. The snow density was measured by snow sampling in a snow pit with a small cylinder, which was weighted using a spring balance. A set of 16 ablation/ accumulation stakes has been monitored continuously since May 2005.
Two digital elevation models (DEMs) used for this study were derived from aerial photographs acquired in September 1999 and 2005 by the Glacier and Permafrost Working Group of the Laboratory of Hydraulics, Hydrology and Glaciology at ETH Zürich, using digital photogrammetry. The horizontal resolutions of the DEMs were 10 m and 25 m, respectively. The absolute accuracy in the horizontal as well as in the vertical direction was 0.6–0.7m. The elevation changes on the glaciated area in the catchment have been estimated from the difference between these two DEMs with an accuracy of about ±1m. Another DEM was generated in November 2006 using airborne laser scanning with a higher resolution (Reference ValletVallet, 2002) but has been gridded to a resolution of 10 m to match the existing DEMs.
Mass-balance modeling
We use the energy-balance model SnowDEM (Reference CorripioCorripio, 2002), coupled with a gravitational MTD routine (Reference GruberGruber, 2007), to model the mass balance. Mass transport caused by wind distribution is not included in the present version of the model. SnowDEM is a distributed, multilayered snow energy-balance model that takes full account of topographic influences and simulates the following fluxes:
-
1. incoming and outgoing shortwave radiation (direct, diffuse and reflected);
-
2. incoming and outgoing longwave radiation (atmospheric thermal radiation and emitted radiation from surrounding slopes);
-
3. snow surface and subsurface temperature; and
-
4. latent and sensible turbulent heat interchange with the atmosphere.
The model is a slight modification of that described in Reference CorripioCorripio (2002), which can be summarized in the following equation expressing the net energy flux at the surface, Q:
where IG is global shortwave radiation, α is albedo, L↓ is downward flux of longwave radiation, L↑ is upward flux of longwave radiation, H and L v E are sensible and latent heat fluxes, Q s is internal heat flux within the snowpack and Q M is available heat for melting.
Coupled with SnowDEM is a mass-conserving algorithm to parameterize gravitational MTD using DEMs (Reference GruberGruber, 2007). In this model, it is assumed that the potential flow from one cell to its neighbor is exclusively dependent upon topography. Only the elevation difference between cells (i.e. potential energy) is used in the flow propagation scheme, and kinetic energy is entirely neglected.
The model is run for the period Sepember 2005–October 2006, corresponding to the date of the DEM generation, so that it can be compared with ice volume loss which is estimated using the difference in elevation. The first model run (MR1) was completed without the MTD routine. A second model run (MR2) was coupled with MTD and the routine was run every time-step at which precipitation was not zero. The model was run using input data from T1, chosen over T2 as it better represents the climate of a glaciated catchment. The lapse rates used for the model were estimated from US National Centers for Environmental Prediction (NCEP) re-analysis data provided by the US National Oceanic and Atmospheric Administration (NOAA) office of Oceanic and Atmospheric Research (OAR) Earth Systems Research Laboratory (ESRL) Physical Sciences Division (PSD), Boulder, Colorado (http://www.cdc.noaa.gov/; Reference KalnayKalnay and others, 1996). A precipitation gradient of 0.8mkm − 1 a − 1 is used.
Results
Contribution from ice-volume loss to runoff: 1999–2005
The estimated loss of ice volume, derived from elevation changes in the DEMs, is approximately (40±5) × 106 m3 for the 6 years from 1999 to 2005 (Fig. 2). Maximum ice-thickness loss of 35 m is at the decaying tongue. This part of the tongue is downwasting melting ice, which is decoupled from the dynamical part of the glacier. The specific net balance for this period is –7.5±1m (of ice). This results in an average annual loss of ice volume of 6.6×106 m3 and an average annual specific net balance of –1.25m (Table 1).

Fig. 2. Difference (m) in elevation over the period 1999–2005 in the glaciated area of the Haut Glacier d’Arolla catchment area. The accuracy is about 1 m. Average ice loss over the glaciated area is 7.5 m. The background is a shaded image of the 1999 DEM.
Table 1. Annual average values of components contributing to runoff for the periods 1999–2005 and 2005–06
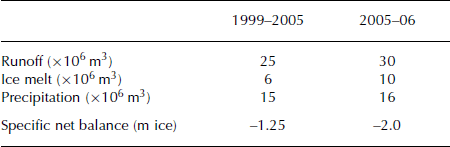
The measured runoff for the same period is 150×106 m3 of water, whereas water generation from ice melt, derived from the volume loss, is (36±5) ×106 m3. Thus, the ice melt contributes about 25% to the annual runoff in the catchment area. The other 75% is either from snowmelt or from rain. This is consistent with our precipitation measurements, which result in a total measured precipitation of 92×106 m3 of generated water inside the catchment. It should be noted
that the measured precipitation can be underestimated by up to 50% due to undercatching in the precipitation gauge during snowfall because of wind. These estimations correspond to 25×106 m3 of annual runoff, 6×106 m3 of annual water generation due to ice melt and 15×106 m3 of annual water generation due to precipitation (Table 1).
Ice velocities
In order to be able to fully interpret the spacial variation depicted in Figure 2, ice dynamics should be considered. We do not address this topic here, but measurements show that the ice flow is rather slow. Measurements of ice velocities in August 2005 (personal communication from D.W.F. Mair) show highest velocities in the upper part of the glacier, with a maximum of 11 ma − 1. The annual velocities are slightly smaller, with a maximum of 10ma − 1.
Contribution from ice-volume loss to runoff: 2005–06
The estimated loss of ice volume, derived from elevation changes in DEMs from 2005 and 2006, is approximately 11×106 m3, with very similar ice ablation distribution in the period 1999–2005 (Fig. 2). The specific net balance is –2m (of ice).
The measured runoff for the period 2005–06 is 30×106 m3, the water generation from ice melt about 10×106 m3 and the estimated precipitation 16×106 m3 (Table 1). For comparison, the measured runoff in the remarkably hot year 2003 was also 30×106 m3, although this year had a much shorter melt season than 2006.
Model results from Snow DEM: 2005–06
Snow DEM was run for the period September 2005–October 2006 using input data from station T1. In the first model run (MR1), MTD was not coupled to SnowDEM. The algorithm was included in the second model run (MR2), however, being executed each time-step where precipitation was greater than zero.
MR1 overestimates the measured runoff by about 40%, while MR2 overestimates the runoff by <10% (Table 2). The difference between MR1 and MR2 is mainly due to runoff generation from snowmelt. The snow-covered area in MR1 is much larger than in MR2, because steep areas have less or no snow in MR2. The difference in ice melt is caused by longer-lasting snow in regions where avalanches occur, and ice is therefore exposed later. The resulting specific net balance for MR1 and MR2 is –2.6ma − 1 and –2.3ma − 1, respectively.
Table 2. Model results for MR1 and MR2, showing the different components of the contribution to runoff in the 2005–06 season
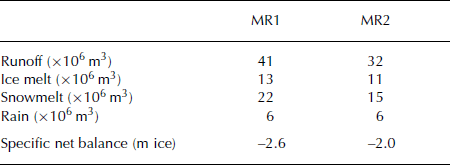
The model results from MR1 are mainly altitude-dependent, while the results from MR2 vary for a given altitude (depending on distance from avalanching slopes). Table 3 shows the comparison between measured and modeled snow water equivalent (SWE) at day 144 for MR1 and MR2. In general, modeled SWE is underestimated in the upper part of the glacier and overestimated in the lower part. Figure 3 shows the ablation/accumulation measurements from the AWS glacier ultrasonic depth gauge against model results from MR1 at the same location. The model’s predictions are accurate for ice melt up until day 210, when snowfall occurs, after which the predictions are less accurate. It is not clear if this inaccuracy is due only to the overestimated albedo after summer snowfall (Fig. 3, dashed line for modeled albedo) or to neglected snow settling in the model.

Fig. 3. Measured ablation (gray line) using an ultrasonic depth gauge against modeled ablation (black line) from the model run including the MTD routine. The dotted line is measured albedo; the dashed line is modeled albedo. No snow settling is included in the model, which makes results after snowfall events difficult to interpret.
Discussion and Conclusion
Ice-volume loss has been estimated using DEMs from different time periods. The maximum ice-thickness loss during a 6 year period (1999–2005) was 7.5 m at the decaying tongue. The specific net balance over the whole glaciated area is −1.25ma − 1 between 1999 and 2005, and −2ma − 1 for the year 2005–06. The estimated ice-volume loss and the estimated precipitation from measurements are in good agreement with runoff measurements.
An energy-balance model including a gravitational MTD routine was run for the period 2005–06. MTD was not included in the first model run (MR1),while itwas fully coupled in the second model run (MR2). MR1 overestimates the measured runoff by about 40%, while MR2 overestimates the runoff by <10%. The contribution of runoff from snowmelt is the main discrepancy between MR1 and MR2. The snow-covered surface becomes smaller when snow is removed from steep slopes, which results in less snowmelt. However, water generation from precipitation is overestimated in both models. One of the reasons for this could be that our model does not include a snowdrift routine. Reference Mernild, Liston, Hasholt and KnudsenMernild and others (2006) show that approximately 12% of the precipitation can be returned to the atmosphere by sublimation of drifting snow. However, including the MTD routine in MR2 remarkably improves the results (both runoff and ice melt). The avalanching routine transports snow from steep walls down onto the glacier, keeps the glacier snow-covered for longer and therefore leads to less ice melt. If ice is exposed earlier, the melt season for ice is longer which enhances ice melt due to the lower albedo of ice.
The difference in modeled and measured mass balance (estimated from DEMs) is caused mainly by differences in snow distribution, which indirectly affect the energy balance by influencing the albedo, reflected shortwave radiation from surrounding slopes and the longwave outgoing radiation. These effects are very important and require further consideration. Figure 3 shows that ice ablation at the location of AWS glacier is in good agreement with measurements, while the time after summer snowfall is represented rather poorly. This is due either to an overestimation of albedo in the model or to the neglected settling, which is represented in the measurement. We have not included snow settling in the model and therefore cannot quantify this effect. Table 3 shows that modeled SWE is generally underestimated by a greater amount in the upper part of the glacier than in the lower part. A possible reason for this might be neglected snow redistribution by wind, and neglected topographical influences on precipitation distribution. The results also show that some avalanches are well represented with MTD (e.g. stakes 6, 9, 11 and 15) while others are overestimated (stakes 4 and 10). Because MTD is only slope-dependent, it neglects snow stratigraphy which is crucial for a correct representation of avalanches. It therefore cannot be used for predicting single avalanche events. However, our results show that it is a very valuable tool for hydrological and glacier mass-balance estimations.
Table 3. Model results for MR1 and MR2 for day 144, compared with measured snow depths on the same day

Our results lead to the conclusion that the distribution of snow is important not only for the timing of streamflow throughout the year, but also for the total amount of water available from a basin (Table 2). The snow distribution has the largest effect on snowmelt, depending on how much snow-covered area is exposed. Furthermore, if the snow is not distributed correctly within the basin, the ice cover will become exposed too early or too late in the season, leading to incorrect estimates of ice melt. It is therefore very important to include other processes in mass-balance models, which can improve the snow distribution inside a catchment. Some of these processes are distribution of snow due to wind, sublimation of drifting snow and the precipitation distribution due to topographical obstacles in steep terrain.
Acknowledgements
We are very grateful to T. Blunschi, H. Bösch, M. Funk, M.G. Haas, P. Jenni, T. Keller, F. Pellicciotti, P. Perona, S. Rim-kus, K. Schroff, C. Senn, R.Weber and T. Wyder. Many thanks to S. Gruber for providing help with MTD. Grande Dixence SA provided the runoff measurements. We also thank M.B. Dyurgerov and S.A. Sokratov for valuable comments and suggestions. The project is carried out under Swiss National Science Foundation grant No. 200021105586.





