Mathematical Modelling
The study of avalanche dynamics started in the former Soviet Union in the 1930s, when the first variants of equations and formulae for avalanche velocity were proposed (for references see Reference EglitEglit (1968)). These equations were based on the treatment of an avalanche as a “material point”. Later, in 1962, there appeared a paper by Reference KozikKozik (1962), widely known in Russia, in which a “material-point” model was revised, developed and described very clearly. In particular, Kozik considered a powder-snow avalanche. To estimate the model coefficients, he supposed an avalanche to have the form of a parabolic cylinder with a given ratio of height and length. However, his theory (as well as that of all others mentioned above) does not contain equations describing the variation of avalanche density and dimensions based on physical laws.
I will not discuss the above-mentioned works here. This paper presents only some results obtained by researchers from Moscow State University.
A mathematical model that treats a powder-snow avalanche as a turbulent flow of a two-component snow–air mixture, and is intended to describe the density and velocity distribution within the avalanche, was proposed in 1974 by A. G. Kulikovskiy and E. I. Sveshnikova (Reference Bakhvalov, Kulikovskiy, Kurkin, Sveshnikova and EglitBakhvalov and others, 1974). The basic equations in the model are the Reynolds’ turbulent equations, together with the hypothesis that the turbulent viscosity and diffusion coefficients are known functions of the distance from the bottom and the integral of the vertical gradient of the mean velocity. This is a modification of the well-known Prandtl hypothesis. The modification is necessary because the vertical profile of flow velocity is not monotonous in an avalanche. The authors performed some test calculations with their model.
It is worth mentioning that at present there is no generally accepted theory for turbulent motion of two-phase flow when gravity is important. The Reference Kulikovskiy and SveshnikovaKulikovskiy and Sveshnikova (1977) model is one possible model. It is simpler than the k − ε model (see, for example, Reference ScheiwillerScheiwiller, 1986) which includes two extra differential equations — for turbulent kinetic energy k and its dissipation ε,
A model that treats an avalanche as a snow-powder cloud of prescribed geometrical form has already been proposed by Reference Kulikovskiy and SveshnikovaKulikovskiy and Sveshnikova (1977). It deals with the mass-center velocity of the cloud, its mean density, its dimensions and form variation during motion. The longitudinal cross-section is assumed to have a half-elliptic form with both diameters varying independently during motion.
The four basic equations of the model allow one to calculate the variation of the center of the mass velocity, length, height and mean density of the cloud. These four equations express that: (1) avalanche volume variation equals the air volume captured by the avalanche; (2) avalanche mass variation is connected with air- and snow-entrainnient, and also with snow-sedimentation; (3) avalanche momentum varies due to gravity, bottom friction, air drag and snow sedimentation, and; (4) kinetic energy of the internal motion and deformation of the cloud is caused by gravity, the air-pressure gradient at the top boundary of the cloud (due to air flow over the cloud) and turbulent diffusion.
Formulae for air- and snow-entrainment rates and for the other coefficients of the model are constructed on the basis of theories of turbulent jets and flows in open channels. For example, the air entrainment rate v 1 is assumed to be proportional to the avalanche velocity v and the square root of the ratio of the air density ρ a and the cloud density ρ
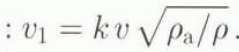
This formula was used by Reference OnufriyevOnufriev (1967) to calculate the motion of a circular vortex representing the front zone of a lifting warm airjei and by Reference KalazhokovKalazhokov (1969) in the theory of motion of an aerosol in a viscous fluid.
It can be justified on the basis of the assumption that air entrainment occurs due to instability of the boundary between an avalanche and the ambient air. It is known (e.g. Reference Landau and LifshitzLandau and Lifshits, 1983) that the rate of growth of disturbances on the boundary between two layers depends on the velocity difference of the layers and on the following combination of the fluid densities ρ 1 and ρ 2.
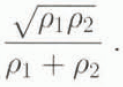
This expression is used in Equation (3) for mass exchange in hydraulic models described below in this paper. If ρ
1 = ρ
a, ρ
2 = ρ and ρ
a ≪ ρ, then it can be approximated by 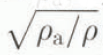 to obtain Equation (1).
to obtain Equation (1).
It should be specially mentioned that the crucial difference between the Kulikovskiy and Sveshnikova model and many other models of a snow cloud, e.g. developed by Reference Beghin, Hopfinger and BrillerBeghin and others (1981), is that the growth rate of an avalanche is not prescribed but is found by solving the basic system of equations.
Many computations have been made using this model. The dependence of the results on the initial conditions and on the values of the model coefficients has been studied. The character of the motion for a variety of conditions has been investigated. For example, it has been found that for a given slope and model coefficients all possible initial conditions can be separated into two domains: a cloud on a constant slope grows if its initial velocity and height are high enough and diminish in the opposite case. It has also been found that the avalanche velocity on a constant slope at first increases with constant acceleration depending on the slope angle. There exists a certain limit of velocity that depends mainly on the initial mass of the avalanche and the amount of snow involved from the slope. After reaching this limit velocity an avalanche decelerates. The details can be found in Reference Kulikovskiy and SveshnikovaKulikovskiy and Sveshnikova (1977) and Reference Eglit and SveshnikovaEglit and Sveshnikova (1980).
The last mathematical model described in this paper is of an hydraulic type. The hydraulic-type momentum equation for avalanches (including powder-snow avalanches) was proposed by Reference VoellmyVoellmy (1955). However, his theory does not include equations for calculating the density and the height of the flow. The momentum equation is treated as an ordinary (not partial) differential equation. The height and the density of the flow are assumed to be given constants along the avalanche body (except the run-out zone, but in that zone the momentum equation is not used and all calculations are based on a simple balance equation of the kinetic and potential energy of an avalanche).
The complete system of equations of an hydraulic type, together with initial and boundary conditions, has been formulated later in Russian researchers’ papers. For dense avalanches, it can be found in Reference Grigoryan, Eglit and Yakimov.Grigorian and others (1967) and Reference EglitEglit (1968), and for powder-snow avalanches as well as for avalanches consisting of two layers (a lower dense layer and an upper powder layer) in Reference Eglit and ShahinpoorEglit (1983), Reference Eglit and Vel’tishchev.Eglit and Vel’tishchev (1985) and Reference NazarovNazarov (1991, Reference Nazarov1992, Reference Nazarov1993).
The two-layer model includes friction and mass exchange at the boundary layers as well as mixing with the ambient air and entrainment of snow from the snow cover. The calculations show that the transformation of a dense avalanche into a powder one can be described by this model.
One of the simplest variants of the governing equations for the two-layer model is written below (Eglit, 1983). These equations describe one-dimensional motion down a wide slope. Equations for channelled avalanches can be found in Reference NazarovNazarov (1991, Reference Nazarov1992, Reference Nazarov1993).
Let ρ 1, v 1, h 1 and ρ 2, v 2, h 2 be the density, velocity and thickness of the dense layer and the powder layer, respectively; ρ 0, h 0—the density and thickness of the underlying snow cover; ρ a—the air density; ψ — the slope angle.
Governing equations for a powder layer are

Here, V 2a, V 21, V s are the rates of change in height due to entrainment of air and snow and sedimentation; τ 2a, τ 21 are friction forces at the snow-powdcr–air boundary and snow-powder–dense layer, respectively.
The equations for a dense layer are

Here, V 10, τ 10 are the rates of height variation and friction force connected with an interaction with the snow cover upon which an avalanche moves.
The equation describing the variation of h 0 is
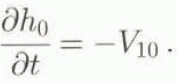
Formulae for the mass exchange between layers:

Here, m a, m 12 and m 01 are empirical coefficients, x f is the coordinate of the leading front of the dense layer of the avalanche.
The bottom friction for the dense layer is assumed to consist of two terms
here f 1 and f 2 are the dry and hydraulic friction, respectively;

Dry friction f 1 is defined by different formulae in the moving (v≠0) and stopped (v = 0) pans of an avalanche

where

In these relations, µ, and k 10 are the dimensionless coefficients of dry and hydraulic friction, respectively; τ * is the upper limit of shear stress in snow cover (Reference GrigoryanGrigorian, 1979).
Numerical investigation of the single-layer and two-layer models has been performed. The contribution of different terms and coefficients of the equations, as well as the initial conditions, have been studied. The ranges of possible values of coefficients have been obtained by comparison between calculated and observed data (Reference Blagoveshchenskiy and EglitBlagoveshchenskiy and Eglit, 1985; Eglit and Vel’tishchev, 1985; Reference NazarovNazarov 1991, Reference Nazarov1992, Reference Nazarov1993; Reference Blagoveshchenskiy, Mironova and EglitBlagoveshchenskiy and others, 1995).
Physical Modelling
Physical modelling of powder-snow avalanches in Russia began in 1967 with Yu. L. Yakimov and I. E. Shurova (Reference Briukhanov and ŌuraBriukhanov and others, 1967). They modeled an avalanche using a flow of steel spheres moving over an incline placed in a water tank. Their main idea was to simulate an avalanche “air wave” as a powerful semi-circular vortex forming in air in front of the main body of an avalanche. They observed such vortices in their experiments.
Later, the same authors continued to study vortices in clear air and in air containing suspended particles of dust (Reference Yakimov and ShurovaYakimov and Shurova, 1988). In particular, they studied the analogy between those parts of an avalanche-front vortex touching the ground and a tornado. They also explained why velocities in an avalanche “air wave” can be much greater than the front velocity of the dense part of the avalanche.
In experiments performed by Sukhanov and Reference Bozhinskiy and SukhanovBozhinskiv (1993,Reference Bozhinskiy and Sukhanov1995a, Reference Bozhinskiy and Sukhanovb) powder-snow avalanches were modeled by a flow of a mixture of aluminium powder and ferromagnetic sawdust over an inclined surface or in a chute. Part of the mixture was placed at the top of the avalanche path and kept at rest by means of an electromagnet. Then, the electromagnet was de-energized and the mixture moved down the slope. The powder part of the avalanche was formed by aluminium powder that was pressed out of the body when it stopped. The form and velocity of the avalanche were measured using a video camera.
All the experiments described above provide a physical insight and certain quantitative dependencies for flows that are analogous to natural powder-snow avalanches. However, they (as well as all of the other known experiments on physical modelling of powder-snow avalanches) cannot be considered as modelling a particular av alanche from start to finish because the similarity criteria needed for this phenomenon are not yet established which is why there is no proof of the similarity of the model and the prototype.
Measurement of Dynamic Parameters of Powder-Snow Avalanches and Comparison with Results of Mathematical Modelling
There are few detailed measurements of the dynamic parameters of natural powder-snow avalanches in motion. Some

were made by researchers from Moscow State University during their stay at the University scientific research station near Mount Elbrus in the Caucasus. In 1969–73, measurements of the dynamic pressure of several powder avalanches were made using force cells placed on poles and trees (Reference UrumbayevUrumbaev, 1974).
In 1974, a system of masts equipped with gauges was constructed under the guidance of N. A. Urumbaev in the path of the so-called “home” avalanche. The velocities and pressures of powder-snow avalanches at different states of motion were measured. Later, the measuring equipment was improved and new data on velocities and also emission of acoustic and seismic signals by powder-snow avalanches were obtained (Reference Grigoryan, Urumbayev and NekrasovGrigorian and others, 1982; Reference Sukhanov and KholobayevaSukhanov and Kholobayeva, 1982; Reference SukhanovSukhanov, 1982). Mathematical modelling of the “home” avalanche, calculation of its pressure-variation with time at certain points of the slope and comparison with measured values was carried out by Reference Nazarov1992Nazarov (1993).
Data on velocities, dimensions and the geometrical forms of several powder-snow avalanches that occurred in the Khi-biny mountains and at Fortambek glacier in the Pamir mountains were obtained using a stereophotogrammetric and filming technique (Reference OnufriyevSamoilov, 1976; Reference BlagovestehenskiyBlagoveshchenskiy, 1990).
Calculation of some of the natural avalanches described above and comparison of calculated and measured parameters have been made using Reference Nazarov1992Nazarov’s (1992) hydraulic model.
Values of the friction, mass exchange and other coefficients for two Fortambek avalanches and for a Khibiny one, used by A. N. Nazarov, are given in the following table. They were chosen to fit the measured data for these particular avalanches and to be in accordance with the range of values fitting the other known data about avalanches and similar phenomena.
Here m a is the coefficient of air entrainment; m 12 and m 02 are coefficients of snow entrainment from the snow cover and from the dense layer by the powder one, respectively; m 01 determines the amount of snow entrained from the snow cover; v s is the vertical velocity of particle sedimentation (vs = V s/ cos ψ); k 20 is the friction coefficient for the powder layer.
The calculated and measured parameters for the stuthed avalanches practically coincide almost everywhere along the avalanche paths, and the orders of the values of the coefficients do not differ for different avalanches. This confirms that the described model can be used for calculation of the dynamic parameters of powder-snow avalanches.

