Introduction
Knowledge of the mass balance of polar ice sheets is essential for understanding sea-level change. The recent assessment from the Intergovernmental Panel on Climate Change Fourth Assessment Report (Reference SolomonIPCC, 2007) summarizes estimates of the mass change from both the Greenland and Antarctic ice sheets from 1993 to 2003 in the ranges from in balance (0 Gt a–1) to a loss of 300 Gt a–1, equivalent to a rate of sea-level rise of 0–0.8mma–1. Other results from satellite and aircraft measurements of surface elevation change (dH/dt), satellite measurements of changes in gravity, and the mass input–output method are reviewed (Reference Alley, Spencer and AnandakrishnanAlley and others, 2007; Reference Shepherd and WinghamShepherd and Wingham, 2007) and tabulated in Reference Dahl-JensenDahl-Jensen and others (2009). A particular issue of concern for deriving mass changes (dM/dt) from observed dH/dt has been the appropriate density to use, because dH/dt is in general a combination of changes in firn thickness and solid-ice thickness, both of which have different densities. Recently Reference ZwallyZwally and others (2011) reported a net mass loss from the Greenland ice sheet of 171±4Gt a–1 for the period 2003–07 and a loss of 7 ±3 Gt a–1 for the period 1992–2002 based on dH/dt observations over these time periods. The methods for these calculations are described in more detail in this paper.
The relation between dH/dt and dM/dt is the result of multiple processes occurring throughout the ice-sheet column. For example, variations in surface air temperature cause a change in the rate of compaction in the upper firn layers, which causes a surface elevation change, but this temperature-driven change does not involve any mass change (Reference Zwally and LiZwally and Li, 2002). Reference Arthern and WinghamArthern and Wingham (1998) evaluated the impact of changes in accumulation rate, temperature and surface snow density by using a firn compaction model. Their results suggested that accumulation-rate induced changes were the most significant, and that temperature effects were relatively small. In contrast, the firn compaction model of Reference Zwally and LiZwally and Li (2002) showed a larger temperature sensitivity due to their introduction of a temperature-dependent activation energy and rate coefficient based on laboratory experiments. Their results showed that the seasonal variation in surface temperature caused seasonal variations in surface elevation, as well as longer-term changes from year-to-year trends in temperature. This strong dependence of firn compaction rate on temperature has since been supported by field observations of compaction rates (Reference Arthern, Vaughan, Rankin, Mulvaney and ThomasArthern and others, 2010).
Prior to Reference ZwallyZwally and others (2011), a constant effective density, ρ eff, with values between 300 and 900 kgm–3 was generally used to convert dH/dt to dM/dt (e.g. 350 in Reference Davis, Li, McConnell, Frey and HannaDavis and others, 2005; 300 for the ‘interior’ and 900 to ‘seaward’ in Reference Thomas, Frederick, Krabill, Manizade and MartinThomas and others, 2006; 350 and 917 in Reference Wingham, Shepherd, Muir and MarshallWingham and others, 2006). However, Figure 1 shows a case in which using a constant density is clearly not valid. Consider a location where the accumulation rate, A(t), is increasing in time while the ice sheet is dynamically thinning (i.e. the firn thickness change dI firn/dt > 0, and the underlying ice thickness change dI ice/dt < 0, with example values of firn and ice thickness changes and associated densities given in Figure 1. The net mass change (per unit area and time) is dM/dt = 200 – 900 = –700 kgm–2 a–1, and the net thickness change is dI/dt = 0.4 – 1.0 = –0.6ma–1. Thus, the effective density using this dI/dt would be ρ eff = (dM/dt)/(dI/dt) = –700/–0.60 = 1167 kgm–3, which is greater than the density of glacier ice, ρ i = 900 kgm–3.
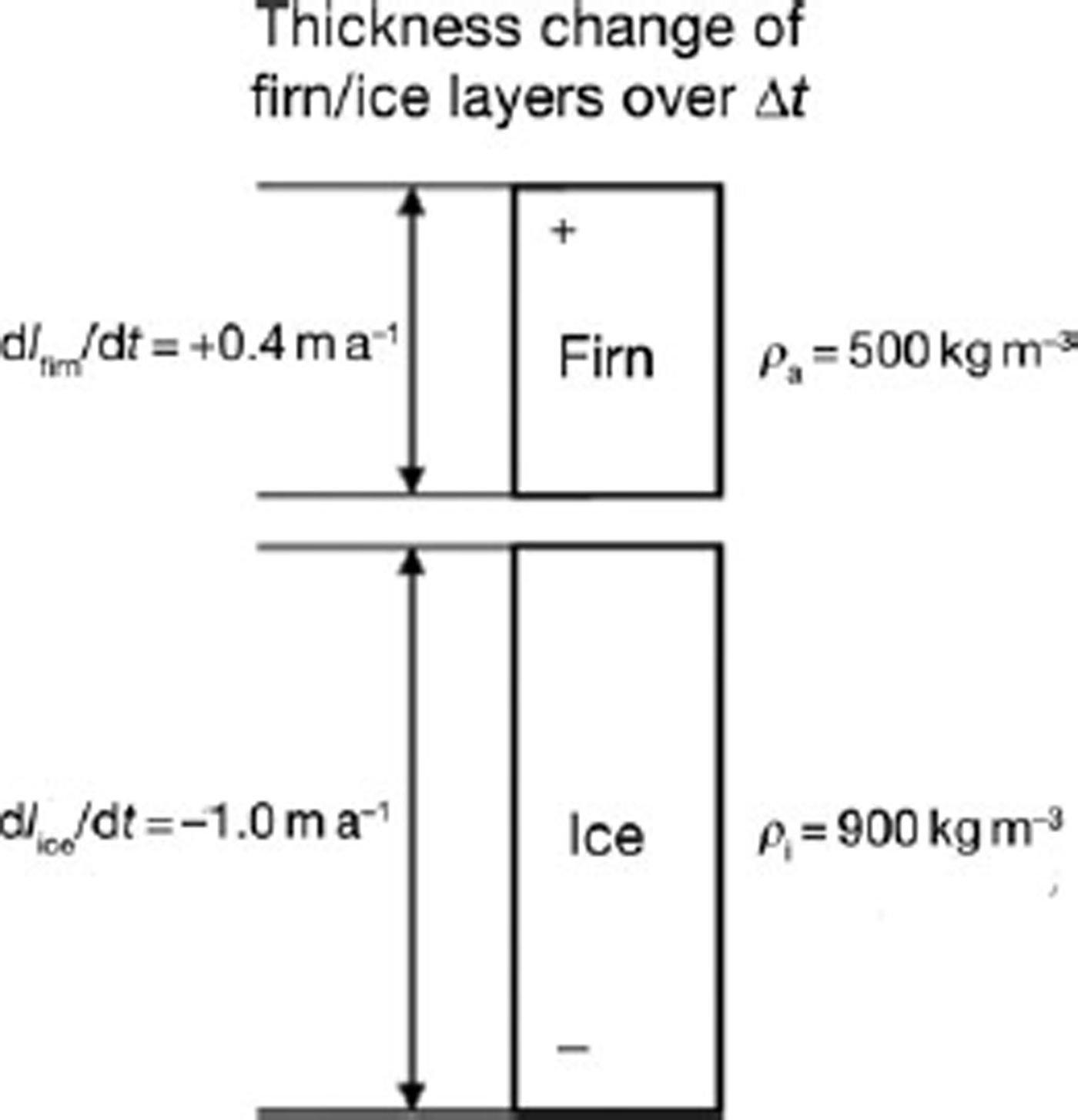
Fig. 1. Example of upper firn and deep ice thickness changes and associated mass changes, where 200 kgm–2 a–1 of firn is added to the firn–ice column by an accumulation increase and 900 kgm–2 a–1 is subtracted by dynamic thinning. In this case, the conventionally defined effective density, ρ eff = (dM/dt)/(dI/dt), is 1167 kgm–3, which would be unrealistically greater than the density of ice.
Our example clearly shows that the assumption that some value of ρ eff between 300 and 900 kgm–3 can be chosen is not always valid. In fact, it will be invalid wherever there is a combination of accumulation-driven thickening and dynamic thinning, or vice versa. Furthermore, where dI firn/dt =dI ice/dt, the corresponding value of ρ eff will become infinite. This example demonstrates the necessity of estimating changes in firn thickness and ice thickness separately, and of using the appropriate densities for each.
In this paper, we present a firn compaction model for calculating changes in the rate of firn compaction caused by changes in both accumulation rate and temperature. The model is used to separate the accumulation-driven and ablation-dynamic-driven changes in surface elevation, and to calculate the appropriate firn density for accumulation-driven changes. It incorporates the processes of surface melting, percolation and refreezing. It also includes a critical improvement to accommodate a time-dependent accumulation rate, A(t). We apply the method to three selected field locations in Greenland.
The Firn Compaction Model
As described in Zwally and Li (2002), the dH/dt of an ice sheet is composed of several vertical-velocity components:
Here accumulation rate, A(t), is the component that raises the surface at a rate of A(t)/ρ sf, where ρ sf is the density of the surface snow. In general, ρ sf has a value of ~330 kgm–3 in dry snow regions (Reference PatersonPaterson, 1994 ). In areas with surface melt, the meltwater percolates downward in the firn layers and the density and thickness of firn layers are modified by the meltwater and refreezing (Li and others, 2007; Reference ReehReeh, 2008). The melting and refreezing process has been incorporated in our model and is described in detail by Reference Li, Zwally and ComisoLi and others (2007). A b(t) is the ablation rate occurring only in the ablation zone, V ice is the vertical velocity of the ice at the firn/ice transition, and dB/dt is the vertical motion of the underlying bedrock. V fc(t) is the velocity of firn compaction at the surface, which is the integral of the compressive displacement of the firn layers over the length of the firn column. Following the normal usage that surface elevation, H, is positive upwards and depth, z, is positive downwards, dH/dt, A and dB/dt are positive upwards and V fc, A b and V ice are positive downwards in Equation (1). According to the mass conservation equation (Reference Li and ZwallyLi and Zwally, 2002), the velocity of firn compaction, V fc, at depth z is given by the density, ρ(z), and compaction rate, dρ(z)/dt, as
where z i is the firn–ice transition depth at which the density is ~900 kgm–3.
Essential to the compaction model is the constitutive relation between the compaction rate, dρ/dt, and the physical variables such as accumulation rate, A(t), and firn temperature, T(t), that drive the density change. This relation is given by
Equation (3) is a semi-empirical relation modified from that initially proposed by Reference Herron and LangwayHerron and Langway (1980) for the steady-state case, and Ā = Ā(t) is the constant accumulation rate in their relation. As discussed by Reference Zwally and LiZwally and Li (2002), Equation (3) is based on the idea that the compaction rate at depth z is determined by changes in overburden pressure, firn temperature and density. However, Equation (3) is not time-dependent with respect to A(t) at the surface. Therefore Ā in Equation (3) cannot simply be replaced by A(t) at z=0. For example, when A(t) at the surface of the ice sheet is zero, the compaction of deeper firn layers continues, but Equation (3) would indicate that the compaction rate is zero at all depths. Since Ā at least in part reflects the changes of overburden pressure, we replace Ā by the integral from the surface to depth z of A(t–Δt)/Δt to represent the average change of the overburden pressure at depth z, where Δt is the time taken for the layer to propagate from the surface to depth z.
The temperature dependence of the compaction rate, dρ(z)/dt, in Equation (3) has been conventionally taken as following an Arrhenius relation, i.e.
where K(T) is the rate factor due to the temperature T in kelvin. K 0 is a constant, E is the activation energy and R is a gas constant. Experimental results of grain growth and ice creep show that the temperature dependence of K(T) is more sensitive than Equation (4) under constant K 0 and E, indicating that E is actually a function of temperature, E(T). Its value increases with temperature (Reference Jacka and LiJacka and Li, 1994). Since both grain growth and ice creep are involved in firn compaction, Zwally and Li (2002) applied the experimental results to their firn compaction model. They indicated that an increasing value of E(T) will decrease K(T) if K 0 is kept constant, which is contrary to the experimental data. Therefore K 0 must also be a function of temperature, K 0(T). They modified Equation (4) for firn compaction by introducing a temperature-dependent activation energy, E(T), and a rate constant, K 0(T), with an adjustable parameter, β, i.e.
The second term on the right-hand side in Equation (5) is the grain growth rate,
given by the experiments (Fig. 2a).

Fig. 2. (a) The temperature dependence of grain growth rate, K G; (b) activation energy, E(T), for grain growth; and (c) the derived rate constant, K 0G, for grain growth as a function of temperature, according to Equation (6) (shown together with E(T) for comparison). Note that the empirical functions in (a) and (b) were initially given by Zwally and Li (2002, figs 3b and a). However, K G was mislabeled as K 0G in their figure 3b.
An error in the text of the Reference Zwally and LiZwally and Li (2002) paper caused confusion in the application of the theory. By using a best fit to the experimental data given by Reference Jacka and LiJacka and Li (1994), Reference Li and ZwallyZwally and Li (2002) derived the empirical expressions of grain growth rate, K G(T), and the activation energy, E(T), as functions of temperature, T (Fig. 2a and b). Both functions were initially given by Zwally and Li (2002, fig. 3a and b). However, K G was mislabeled as K 0G. Rearranging Equation (6) we have

Fig. 3. A map showing three selected test locations: A (79.4˚ N, 319.9˚ E), B (72.9˚ N, 321.28 E) and C (61.9˚ N, 315.9˚ E) on the Greenland ice sheet. The climatic characteristics for the three locations are given in Table 1.
Figure 2c gives the empirical form of K 0G(T) as a function of temperature by substituting the expressions of E(T) and K G(T) shown in Figure 2a and b into Equation (6), together with the function of E(T). As shown by Figure 2c, K 0G increases with temperature apparently faster than E(T), indicating the stronger temperature dependence of K 0G(T) compared to E(T). Combining Equations (4–6), we then have
where β is an adjustable parameter determined by fitting modeled density profiles to field measurements. Equation (8) accounts for the temperature dependence of grain growth and ice creep rates on firn compaction. It leads to much higher temperature sensitivity than Equation (4) under constant values of K 0 and E (e.g. Reference Herron and LangwayHerron and Langway, 1980), particularly for temperatures higher than –10˚ C. Equations (1–8) are coupled with a one-dimensional heat-conducting equation and solved using the multilayer system described by Reference Zwally and LiZwally and Li (2002).
The empirical parameter, β, in Equation (5) is used to calibrate modeled density profiles to field measurements. In our previous version of the model, we presented β as a function of the annual mean temperature based on field density profiles from Greenland (Reference Li, Zwally, Cornejo and YiLi and others, 2003). Reference HelsenHelsen and others (2008) extended this relation by using 41 observed pore close-off depths (depth of the 830 kgm–3 density) from Antarctica where firn temperatures are much colder. They found a slightly different relation between β and the annual mean temperature. However, for temperatures higher than about –30˚ C (e.g. Greenland), the two relations are similar. To further improve the calibration, we use two critical points at densities of 550 and 830 kgm–3 as the control, and tune the value of β to force the modeled ages at these two densities to match those given by Reference Herron and LangwayHerron and Langway (1980) that were well constrained by the field density measurements. Although the previous calibrations (Reference Li, Zwally, Cornejo and YiLi and others, 2003; Reference HelsenHelsen and others, 2008) showed that β is a function of annual mean temperature only, our tests indicate that the accumulation rate also had an influence, similar to the Herron and Langway (1980) density–age relation for which both temperature and accumulation rate were involved. Our present values of β as a function of annual mean temperature, T m (˚ C), and long-term accumulation rate, ⟨A⟩ (m a–1), for Greenland are


Equations (9) and (10) produce modeled density–depth (age) profiles that are in agreement with those from Reference Herron and LangwayHerron and Langway (1980) within an error <±1%.
Elevation Change Components from Altimetry dH/dt
As described in Equation (1), the surface elevation change, dH/dt, is due to a combination of vertical velocity components from different processes. For non-steady state, these components can be represented by perturbations from steady state, assuming that dB/dt is constant during the measurements:
where dH a/dt = (A(t) – ⟨A⟩)/ρ sf is the direct change caused by A(t), dC AT/dt=–(V fc(t)–⟨V fc⟩) is the firn compaction-rate caused elevation change driven by both A(t) and T(t), dH b/dt=–(A b(t)–⟨A b⟩)/ρ i is driven by changes in the ablation rate, and dH d/dt=–(V ice(t)–⟨V ice⟩) is driven by dynamic changes in the ice flow relative to ⟨A⟩. The hi symbol indicates long-term averages of the various components, obtained during our model spin-up to a steady state. We consider that ablation is zero in the accumulation zone where firn exists. In the ablation zone where there is no firn, accumulation is zero. In general, dC AT/dt depends on the history of both A(t) and T(t) as their effects propagate into the firn. We separate their effects by assuming
where dC A/dt and dC T/dt are changes driven by A(t) and T(t), respectively. The total elevation change from both A(t) and T(t) perturbations becomes
where dH a CA/dt is the total change caused by A(t), including both the direct change and that associated with the compaction rate. Equation (11) then gives
where dI/dt is the net thickness change in the firn/ice column, defined by treating dB/dt and dCT/dt as corrections to dH/dt. dH bd/dt is the combined ablation and dynamic term (as dH bd/dt≡dH d/dt+dH b/dt). In the ablation zone where there is no firn, dH bd/dt is the mixed term of both dynamics and melting (ablation). In the accumulation zone, dH bd/dt is only the dynamic term. The two terms on the right-hand side in Equation (12) involve change in mass. To obtain dH a CA/dt, our compaction model first calculates dH a CAT/dt using both T(t) and A(t), and then calculates dC T/dt using T(t) with constant ⟨A⟩. The dH a CA/dt is then given by
i.e. the total accumulation-driven change in surface elevation is obtained by subtracting the temperature-driven compaction from that caused directly by the change in accumulation rate and by the change in compaction rate driven by both accumulation and temperature variations.
Mass Change from dH/dt Components
Applying appropriate densities to Equation (12) on the right-hand side, the mass change rate, dM/dt, of the ice sheet is given by
The appropriate density associated with the dynamic and ablation term, dH bd/dt(m a–1), is the density of glacier ice (900 kgm–3). The density, ρ a (kgm–3), associated with the shorter-term change of dH a CA/dt(ma–1) is discussed in the next section. In terms of dI/dt (m a–1), Equation (13) can be written as
Equation (14) is used to calculate the mass change of the ice sheet. It requires the altimetry measurements of dH/dt, surface temperature T(t) and accumulation rate A(t) histories as inputs to the compaction model to obtain dC T/dt, dH a CA/dt and the density, ρ a. Reference PatersonEquation (14) indicates that using dI/dt with the density of ice to derive dM/dt is an approximation that neglects the effects of recent changes in accumulation rate on the rate of firn compaction.
Deriving Density, ρa , for dHca a /dt
The density, ρ a, associated with dH a CA/dt shown in Equations (13) and (14) is the average density caused by perturbations to the accumulation rate over a specified time period. Considering the surface elevation change driven by variations in accumulation rate A(t) only, i.e. dH/dt = dH a CA/dt, the corresponding mass change, ΔM a(t), over Δt = t – t 0 is given by
Here A(t) and (A) are in units of kgm–2 a–1. ΔM a(t) is in kgm–2. This mass change causes a surface elevation change of
Thus,
Equation (15) defines the density, ρ a, that is obtained using the firn compaction model. It represents the density of the firn that has been added (removed) as a result of an increase (decrease) in A(t) relative to the density profile for the longterm average ⟨A⟩. However, the corresponding change in the amount of firn and the compaction rate is distributed throughout the firn column, so there is no associated physical layer in the firn with a density ρ a and thickness dH a CA/dt.
Results and Discussion
The appropriate method to derive the mass change, dM/dt, is described by Equation (14). Here we derive the values at three selected locations on the Greenland ice sheet (Fig. 3). Site A is in the northern region and is associated with lower accumulation rate and temperature. Site B is near the Summit of the ice sheet, and site C, in the south, is associated with much higher accumulation rate and temperature. We use monthly surface temperatures, T s(t), for January 1982–October 2007 as shown in Figure 4a from the Advanced Very High Resolution Radiometer (AVHRR) (Reference ComisoComiso, 2003). We parameterize changes in the accumulation rate, A(t), according to the annual mean surface temperature at the rate of 5%K–1. The IPCC report (Reference SolomonIPCC, 2007) summarized the sensitivity of accumulation rate to temperature with a range 4.7–8.5% K–1. Data from Greenland ice cores (Reference Clausen, Gundestrup, Johnsen, Bindschadler and ZwallyClausen and others, 1988) give a range 4–6% K–1 based on a sensitivity of δ18O to temperature of 0.69%δ18OK–1 (Reference Zwally and GiovinettoZwally and Giovinetto, 1997). For 1988–2005, this parameterization gives an average A(t) increase of 0.6% a–1. This is close to the 0.7% a–1 for 1988–2004 inferred from a regional-climate and surface mass-balance model for the percolation and dry-snow zones of Greenland (Reference BoxBox and others, 2006). Although there is a good relation between changes in accumulation and temperature for annual mean values, the correlation could be poor for short-term changes (Reference Kapsner, Alley, Shuman, Anandakrishnan and GrootesKapsner and others, 1995). Therefore, in our A(t) parameterization, we use the annual mean temperatures instead of monthly temperatures to avoid introducing seasonal variations in A(t) due to strong seasonal variations in temperature. A more sophisticated approach that would avoid some of these complications in the sensitivity between temperature and accumulation rate would be to use A(t) from the climate models (e.g. Reference HelsenHelsen and others, 2008).

Fig. 4. (a) Mean monthly surface temperature at site B in Greenland (Fig. 3) showing the general warming during the last two decades. (b) The associated increase in accumulation rate as a function of the annual mean temperature using a rate of 5%K–1. (c) The modeled surface height changes in three components (as marked) from firn compaction driven by temperature and the accumulation rate histories shown in (a) and (b).
Starting from the initial steady-state spin-up, we applied the time series of T s(t) and A(t) to our compaction model. Figure 4c shows the modeled time variations in the three components from firn compaction at site B, driven by the variations in T s(t) and A(t) shown in Figure 4a and b. The profiles show significant interannual variations, especially since 2000 due to the enhanced warming in that period. Although the input temperatures are monthly mean values, the annual cycles in the temperature profile still cause seasonal variations in C T(t) and H a CAT(t) profiles, but with smaller amplitudes (~2 cm) compared to the results from model runs using hourly or daily timescales (Reference Zwally and LiZwally and Li, 2002). In contrast, the H a CA(t) profile does not have seasonal variations, because our parameterization of A(t) does not have a seasonal variation. We use best fits to the profiles in Figure 4c for site B (and the similar profiles for sites A and C), for the period October 2003–October 2007, to obtain the mass change rates, dM/dt, and associated components for the three sites as summarized in Table 1. The associated dH/dt are derived from Ice, Cloud and land Elevation Satellite (ICESat) measurements for the same period, and dB/dt were averaged from three models as in Reference ZwallyZwally and others (2005). As shown in Table 1, the impacts from the temperature- and accumulation-driven components, dC T/dt and dH a CA/dt, are of similar magnitudes, but the temperature increase causes a surface elevation decrease that is offset by the increase in the accumulation rate. At site C, the measured surface elevation change, dH/dt, is –0.083ma–1 and dH a CA/dt is 0.104 ma–1, indicating that the obtained mass loss (–61.7 kgm–2 a–1) is due to the ice-dynamic imbalance and/or ablation. Also, we note that for site C the values of dM/dt and dI/dt from Table 1 give a conventionally defined effective density of 1762 kgm–3, which is greater than the density of ice as in the example of Figure 1.
Table 1. The climatic characteristics and the derived rates of the mass change, dM/dt, and associated values of the components of elevation change as described by Equation (14), together with other parameters for three selected locations (Fig. 3) on the Greenland ice sheet. Calculation of dM/dt requires determination of the accumulation-driven component, dH a CA/dt, and its associated density, ρ a, and the ice-dynamic- and ablation-driven component, dH bd/dt, with density of 900 kgm–3, as well as correction of the observed dH/dt for temperature-driven variations in firn compaction, dC T/dt, and bedrock motion, dB/dt

Once the components required for dM/dt in Equation (14) are known, the average physical density can be calculated using

Together with Equation (12), Equation (16) describes the relationship between the net firn/ice thickness change, dI/dt, and the total thickness change (|dH a CA/dt| + |dH bd/dt|) associated with the derived densities. When dH a CA/dt and dH bd/dt have the same sign, ρ avg equals ρ eff (=dM/dt/dI/dt) and the conventional method (dM/dt = ρ effdI/dt) would give an arithmetically valid mass change. However, when dH a CA/dt and dH bd/dt have opposite signs (e.g. Reference Alley, Spencer and AnandakrishnanFig. 1 and Table 1 for site C), the conventional method is not valid. Equation (16) shows the importance of separating total thickness change into firn thickness change and ice thickness change. The derived ρ avg for the three sites are summarized in Table 1, together with the corresponding values of ρ eff for comparison. The comparison shows that ρ avg is a more meaningful parameter than ρ eff, but neither ρ avg nor ρ eff can be used to convert dI/dt or dH/dt to dM/dt.
Positive values of dH bd/dt for sites A and B as shown in Table 1 indicate that the ice flow is less than required to balance the long-term average (A), which results in dynamic thickening in the same manner as negative dH bd/dt results in dynamic thinning. The distribution of accumulation-driven changes and dynamic-/ablation-driven changes of the ice sheet, and changes in those parameters with time are described by Reference ZwallyZwally and others (2011).
Conclusion
Altimetry-derived surface elevation changes, dH/dt, can be divided into the components driven by the variations in the following: short-term accumulation rate (i.e. dH a CA/dt), surface temperature (i.e. dC T/dt), ice-dynamic imbalance and ablation (i.e. dH bd/dt) and bedrock motion (i.e. dB/dt). Partitioning altimetry-derived surface elevation change allows assessment of the impacts from recent climate variations versus those from long-term ice-dynamic changes, leading to more accurate estimations of ice-sheet mass balance. Along with 900 kgm–3 for the dynamic-/ablation-driven changes, our calculated densities for the accumulation-driven changes range from 410 to 610 kgm–3, corresponding to average densities, ρ avg, ranging from 680 to 790 kgm–3. In the locations where thickness changes in the firn and ice layers are in opposite directions, the net thickness change as derived from the observed dH/dt cannot be transformed into mass change simply by using a constant average (or effective) density (i.e. a value between 300 and 900 kgm–3).
Acknowledgements
This research was supported by NASA’s ICESat Project Science funding. We thank S.F. Price and two anonymous referees for their valuable comments, which helped greatly to improve the paper.






