Introduction
The construction of a general mathematical model describing mechanical properties is a complicated problem, because all types of mechanical motions occur inside the snowpack. A snowpack consists of layers with different mechanical properties. The ice matrix of each layer is built with grains and bonds. Snow cohesion depends on the number of bonds per grain (coordination number) ik. Grains and bonds are connected in chains. The mechanical properties depend also on the crystallographic orientation of the chain crystals. Formation of the texture is also a result of gravity action. The chains belonging to a loading line parallel to the gravity vector, i.e. the crystals of the chains, can be divided for simplicity into two classes: load-bearing crystals with vertical connections (bonds) and crystals without vertical contacts. The crystals without load serve as material for load-bearing crystal growth. Surface-free energy of load-bearing crystals is higher through its deformation, and the bond radius increases through its flow under loading. Both these factors lead to evaporation of the smaller crystals and further growth of the crystals with bigger radii. Evaporation of the non-load-bearing crystals and a decrease in the coordination number leads to formation of so-called weakening zones with fibrous texture. These zones are finally fragile, and evaporation of the small crystals leads to mechanical anisotropy and decrease of rigidity. Depth-hoar crystals often form chains of load-bearing crystals (Reference SamoylyukSamoylyuk, 1992). Settling of snow can be imagined as follows: vertical bonds are shortened with increase of the diameter due to slow deformation. Collapse of snow layers occurs in the case of the fast loading when load is larger than strength. After collapse a new structure is formed in these layers.
Some weakening zones and depth-hoar zones appear inside the snowpack due to metamorphic processes and recrystallization. Depth-hoar zones are characterized by anisotropy of the connection properties: good bonding in the vertical direction and small in the horizontal direction. Avalanche sliding surfaces were observed at depth-hoar layers with thickness equal to one grain size (Reference Zhidkov, Oleynikov and SamoylovZhidkov and others, 1992). Sometimes the thickness of the layer can be up to about 0.5 m (Reference BolovBolov, 1982). Structural parameters (grain radius, normal and horizontal bond diameter and length, coordination number) are related to temperature, density and sublimation rate and can be calculated using the proposed model.
The current paper is based on a revised version of the mathematical model describing the non-uniform stratified snow cover (Reference Golubev, Guseva, Voytkovskiy and DyurgerovGolubev and Guseva, 1987; Reference Guseva and GolubevGuseva and Golubev, 1989, Reference Guseva and Golubev1990; Reference Guseva-LozinskiGuseva-Lozinski, 1997, Reference Guseva-Lozinski, Inan and Markov1998, Reference Guseva-Lozinski, Hutter, Wang and Beer1999; Reference Golubev and FrolovGolubev and Frolov, 1998). The main difference between this approach and other work is that the equations include macro- and micro-diffusion and describe ice-matrix element changes. This approach enables calculation of the structural variability due to temperature changes and to inhomogeneous snow. The structural model was extended for new snow (Reference Guseva-Lozinski, Hutter, Wang and BeerGuseva-Lozinski, 1999). The mechanical properties in relation to structural properties are the focus of the present study. A two-dimensional non-uniform snowpack is considered. The origin of the normal to snow surface axis z = 0 is defined at a depth H(t) in the soil, and the horizontal axis × is parallel to the main slope direction (Fig. 1). The snow consists of layers with different densities, temperatures and structural and mechanical properties. Detailed study of structure, texture and mechanical properties is necessary for adequate modelling. Snowpack stability depends on individual layer properties. Using average values can be misleading. Settling, and hence densification, of deposited snow increases strength. Stabilization can be defined by the concurrence of strengthening due to densification and stress increase by new snow. Avalanches often occur when the rate of the second process is too fast. Observations show (Reference VoytkovskiyVoytkovskiy, 1977) that the result of slow, small and short-time snowpack loading is deformations which can be described as elastic or viscous deformations. The model requires the following initial and boundary data: variation of the air temperature, solid precipitation, wind speed and air pressure, meteorological data of the snowstorm conditions (maximum and minimum wind speed, gust frequency), air humidity, sun radiation, the snow albedo and heat parameters, the heat parameters of thawing and melting soil and the slope geometric parameters (slope angle).
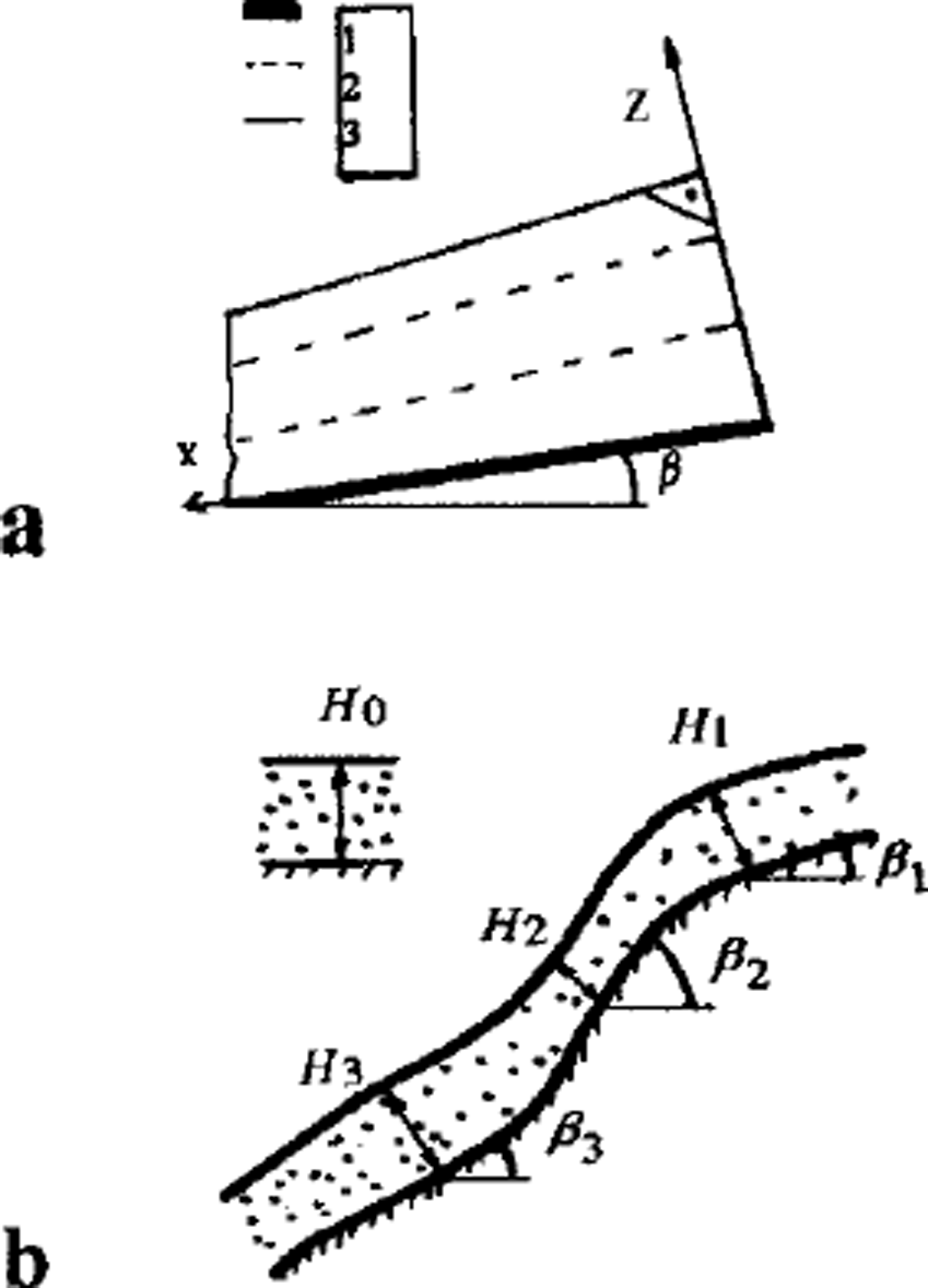
Fig. 1. Two schemes of the layered snowpack on the slope, (a) Two-dimensional axis system (x, Z). (3 is slope angle. 1. Ground-snow boundary; 2 layer boundaries; 3 snowpack surface H(t). (b) Normal sections of the snow cover. Hi(t) are snowpack thickness at the points with different slope angles Hi(t),i= 1,2,3.
Model Description
A two-dimensional layered snowpack is considered and the axes (x,z) are chosen as given in Figure 1. Snowflakes in a freshly deposited layer are transformed into ice grains by metamophic processes, and bonds form between them due to metamorphic processes (micro- and macro-diffusion) and deformation under snow loading.
The porous ice matrix can be approximated by isometric spheres with average radius r connected by cylindrical bonds of lengths ln h and diameters dn h in the horizontal (subscript "h") and normal (subscript "n") directions (Fig. 2a). The temperature field T was calculated by the heat-balance equation with windpumping (Reference AlbertAlbert, 1993) and boundary conditions (Reference Guseva-Lozinski, Inan and MarkovGuseva-Lozinski, 1998). The influence of the windpumping on the metamorphic processes was analyzed using Darcy’s law (Reference ColbeckColbeck, 1997). The rate of sublimation is defined through the processes of macro- and micro-diffusion (Reference Yosida and KingeryYosida, 1963) and convective flux (windpumping) in the pore space:
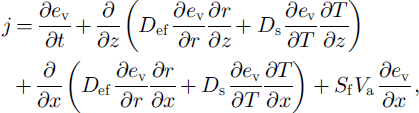
where ev is average water-vapor pressure, Def and Ds are coefficients of micro- and macro-diffusion, t is time, and j = j+ + j ― is the sum of the positive part of the mass transfer (corresponds to condensation) and negative part of the mass transfer (corresponds to evaporation) above the common sublimation/evaporation surface Sf of the grains and bonds per unit of volume. The equilibrium water-vapor density above ice-matrix elements with curvature r and with coefficient of the different surface shape F at temperature T is defined by the Magnus condition for snow crystal (Reference Golubev, Guseva, Voytkovskiy and DyurgerovGolubev and Guseva, 1987): e(T,r)=e(T)(1+F/r) based on the Clapeyron equation (Reference Hobbs and MasonHobbs and Mason, 1964; Reference ColbeckColbeck, 1980). Surface shape parameter F varies from 0 ≤ F ≤ 2 × 10–5 and enables the model to take into account the water-vapor pressure oversaturation around faceted crystals (depth hoar), dendricity and overriming (fresh snow) and rounded grains (small and wet grains) (Reference Guseva-Lozinski, Hutter, Wang and BeerGuseva-Lozinski, 1999). Using the Arrhenius relation for growth rate of the ice-matrix elements, the Darcy speed of the airflow Va and the Magnus condition, it is possible to write the conditions for redistribution of j on the structural elements and definition of average water-vapor pressure in porous space: rate of sublimation/evaporation on the surface of the grain j z , on the surface of the vertical bonds Jn and on the surface of the horizontal bonds jb as follows:
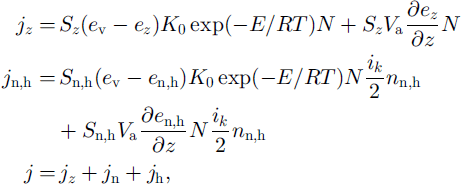
where nn
+ nh = 1, nn
and nh
being the ratio of normal and horizontal bonds, respectively, per grain, N is the average grains number per volume, ik
is a coordination number, E is activation energy, R is gas constant, K0
is the coefficient of the ice-matrix elements growth, Va
is Darcy flow due to windpumping, sublimation surface of the vertical and horizontal
![]() Snh πdn,hln,h, bonds is = sublimation surface of the grain is is the water-vapor pressure above horizontal and vertical bonds, and ez
is the water-vapor pressure above grains (Magnus relation). Here we use the hypothesis that the sublimation rate on the surface of the ice-matrix elements is the result of the difference between average water-vapor pressure in pore space and concentration above the structural elements and sublimation or condensation due to windpumping. The system of equations of the mass transfer within new snow and depth hoar and definition of the average water-vapor pressure in porous space has been described by Reference Guseva-Lozinski, Hutter, Wang and BeerGuseva-Lozinski (1999). The normal and horizontal bonds viscous-plastic flow, the condition of
Snh πdn,hln,h, bonds is = sublimation surface of the grain is is the water-vapor pressure above horizontal and vertical bonds, and ez
is the water-vapor pressure above grains (Magnus relation). Here we use the hypothesis that the sublimation rate on the surface of the ice-matrix elements is the result of the difference between average water-vapor pressure in pore space and concentration above the structural elements and sublimation or condensation due to windpumping. The system of equations of the mass transfer within new snow and depth hoar and definition of the average water-vapor pressure in porous space has been described by Reference Guseva-Lozinski, Hutter, Wang and BeerGuseva-Lozinski (1999). The normal and horizontal bonds viscous-plastic flow, the condition of
![]() strain rate, is as follows: The bond volume varies only due to sublimation or condensation. The bond-diameter variation is the result of all of the processes-sublimation, condensation, viscous flow-and can be written as:
strain rate, is as follows: The bond volume varies only due to sublimation or condensation. The bond-diameter variation is the result of all of the processes-sublimation, condensation, viscous flow-and can be written as:
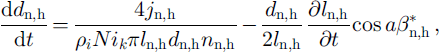
where the relative viscous-plastic deformation coefficients of a cylindrical model beneath overlying-snow constant load
![]() action can be written as εn h = [KρP
2 / ( l + | T | K h ] (Reference VoytkovskiyVoytkovskiy, 1977),
action can be written as εn h = [KρP
2 / ( l + | T | K h ] (Reference VoytkovskiyVoytkovskiy, 1977),
![]() ,
,
![]() 3, fo = sin (3 and Kp = 7.56 × KTnt. The normal relative contact section is σn h = 0.25 (ρs/ρ1)
3, fo = sin (3 and Kp = 7.56 × KTnt. The normal relative contact section is σn h = 0.25 (ρs/ρ1)
![]() where structural coefficients are knh= 0.5 dn,h/r and bnh=(2r+l) A and a are the main direction of the ice-matrix orientation, and
where structural coefficients are knh= 0.5 dn,h/r and bnh=(2r+l) A and a are the main direction of the ice-matrix orientation, and
The coordination number is
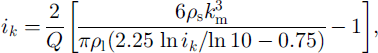
where average structural coefficients are km = 0.5(kn + kh)
![]() and The grain-diameter growth is a result of the coarse-grains growth due to the ice-matrix fine-parts sublimation and due to windpumping:
and The grain-diameter growth is a result of the coarse-grains growth due to the ice-matrix fine-parts sublimation and due to windpumping:
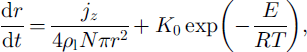
where N=3ps[4p4(1+5)] is the number of grains per unit volume. Structural coefficients vary inside snowpack and are defined for the elastic case in Reference GolubevGolubev (1982) and Reference Golubev and FrolovGolubev and Frolov (1998). Snow density can be defined as follows (Reference Yosida and KingeryYosida, 1963, Reference VoytkovskiyVoytkovskiy, 1977):
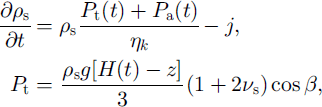
where Pa is atmospheric pressure change and Ps is overlaying snow load. The compressive viscosity coefficient ηk depends exponentially on the snow density Ps for granular snow (Reference Yosida and KingeryYosida, 1963) (100–500 kg m–3) and depends for new snow and for depth hoar as power function on ρs (Reference Endo, Ohzeki and NiwanoEndo and others, 1990; Reference Kominami, Endo, Niwano and UshiodaKominami and others, 1998). The Poisson ratio for snow is
where ratio for ice is vi, ≈ 0.36 and C = 0.25(*fc ― 2), ik ≤ 6 and C = l,ik>6. The Young’s modulus for snow and for ice is
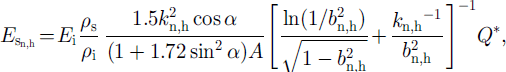
where Ei ≈ 107 kPa (Reference GolubevGolubev, 1982). The initial layer boundaries are defined by the solid-precipitation thickness. The location changes of the layer boundaries can be defined through density changes and common sublimation rate j at the layer boundaries.

where hi(t,x), Pi(t,z,x), and hi(t+Δt,x) are height and average density of the layer with number i(i≥1) at time t
![]() and is the snow-mass change through sublimation/evaporation, and At is the time interval. The snowpack thickness changes through the snow densification and by sublimation processes and can be described as follows:
and is the snow-mass change through sublimation/evaporation, and At is the time interval. The snowpack thickness changes through the snow densification and by sublimation processes and can be described as follows:
![]() where m is current layer number in the snowpack and h’(t) is the solid-precipitation height. The layer thickness decreases with time due to densification. A decreasing rate at depth z can be estimated with the relative deformation coefficients
where m is current layer number in the snowpack and h’(t) is the solid-precipitation height. The layer thickness decreases with time due to densification. A decreasing rate at depth z can be estimated with the relative deformation coefficients
![]() We assume here that the grain strength is larger than the bond strength. Slow deformation increases shear strength due to consolidation. The bonds break under loading larger than the strength limit. Using Equation (3), the current values of bond parameters can be calculated. Based on critical-strength estimations for different loading scenarios of bonds (Reference Zhidkov, Oleynikov and SamoylovZhidkov and others, 1992), the ice Young’s modulus Ein,h
and relative contact sections, the following relations can be estimated for depth-hoar zones (Fig. 2a1-b3):
We assume here that the grain strength is larger than the bond strength. Slow deformation increases shear strength due to consolidation. The bonds break under loading larger than the strength limit. Using Equation (3), the current values of bond parameters can be calculated. Based on critical-strength estimations for different loading scenarios of bonds (Reference Zhidkov, Oleynikov and SamoylovZhidkov and others, 1992), the ice Young’s modulus Ein,h
and relative contact sections, the following relations can be estimated for depth-hoar zones (Fig. 2a1-b3):
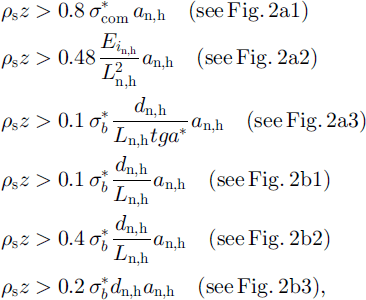
where
![]() is the limit of the ice compression strength,
is the limit of the ice compression strength,
![]() is the limit of ice shear strength (Reference Zhidkov, Oleynikov and SamoylovZhidkov and others, 1992) and Ln,h is the average length of columns without horizontal bonds ’(Fig. 2c). Figure 2a1-a3 is compression, and Figure 2bl-b3 shear loading.
is the limit of ice shear strength (Reference Zhidkov, Oleynikov and SamoylovZhidkov and others, 1992) and Ln,h is the average length of columns without horizontal bonds ’(Fig. 2c). Figure 2a1-a3 is compression, and Figure 2bl-b3 shear loading.
![]() Calculating the relative contact areas σn and using and
Calculating the relative contact areas σn and using and
![]() the moment of collapse can be estimated (Reference VoytkovskiyVoytkovskiy, 1977; Reference GolubevGolubev, 1982). The values of the parameters T,ρs,r, an,h,dn,h
and ln,h are calculated based on Equations (1–7). Calculating snow-stability parameters shows that the shear deformation is more dangerous than compression. The bond fracture is accompanied by settlement of snow and collapse of the snow layer (Fig. 2a4 and b4). Snow thickness is reduced to the length of fractured vertical bonds.
the moment of collapse can be estimated (Reference VoytkovskiyVoytkovskiy, 1977; Reference GolubevGolubev, 1982). The values of the parameters T,ρs,r, an,h,dn,h
and ln,h are calculated based on Equations (1–7). Calculating snow-stability parameters shows that the shear deformation is more dangerous than compression. The bond fracture is accompanied by settlement of snow and collapse of the snow layer (Fig. 2a4 and b4). Snow thickness is reduced to the length of fractured vertical bonds.
Deformation due to loading changes as a result of windpumping was considered (Reference VoytkovskiyVoytkovskiy, 1977):
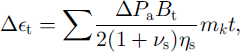
where Δ∊t is the deformation in windy conditions, APa is windpumping loading, Bt is the creep function, mk is the gust frequency, Vs is the shear viscosity coefficient and Vs is the Poisson ratio. The structure anisotropy in vertical and horizontal directions defines the thermomechanical properties of the snow. Sufficient mechanical anisotropy is observed within freshly deposited snow and depth-hoar layers. The ice matrix formed by fresh-snow grains is characterized by a chaotic structure. The curvature radius is larger in the horizontal than in the vertical direction. The metamorphic processes lead to increased normal bond diameters and reduced horizontal bond diameters. Further structural evolution leads to formation of the fibrous structure and depth hoar. An important feature of the depth-hoar layer and freshly deposited snow is an irregular grain-surface shape which accelerates mass transfer due to metamorphism. The equations of this case of mass transfer are defined in Reference Guseva-Lozinski, Hutter, Wang and BeerGuseva-Lozinski (1999). The structural coefficients of the columns X(z) (ratio of normal and horizontal bond diameter) and ζ(z) (ratio of normal and horizontal contact sections) are changed in the interior snowpack and calculated with the conditions for an, h and dn h, and may be used as anisotropy coefficients.
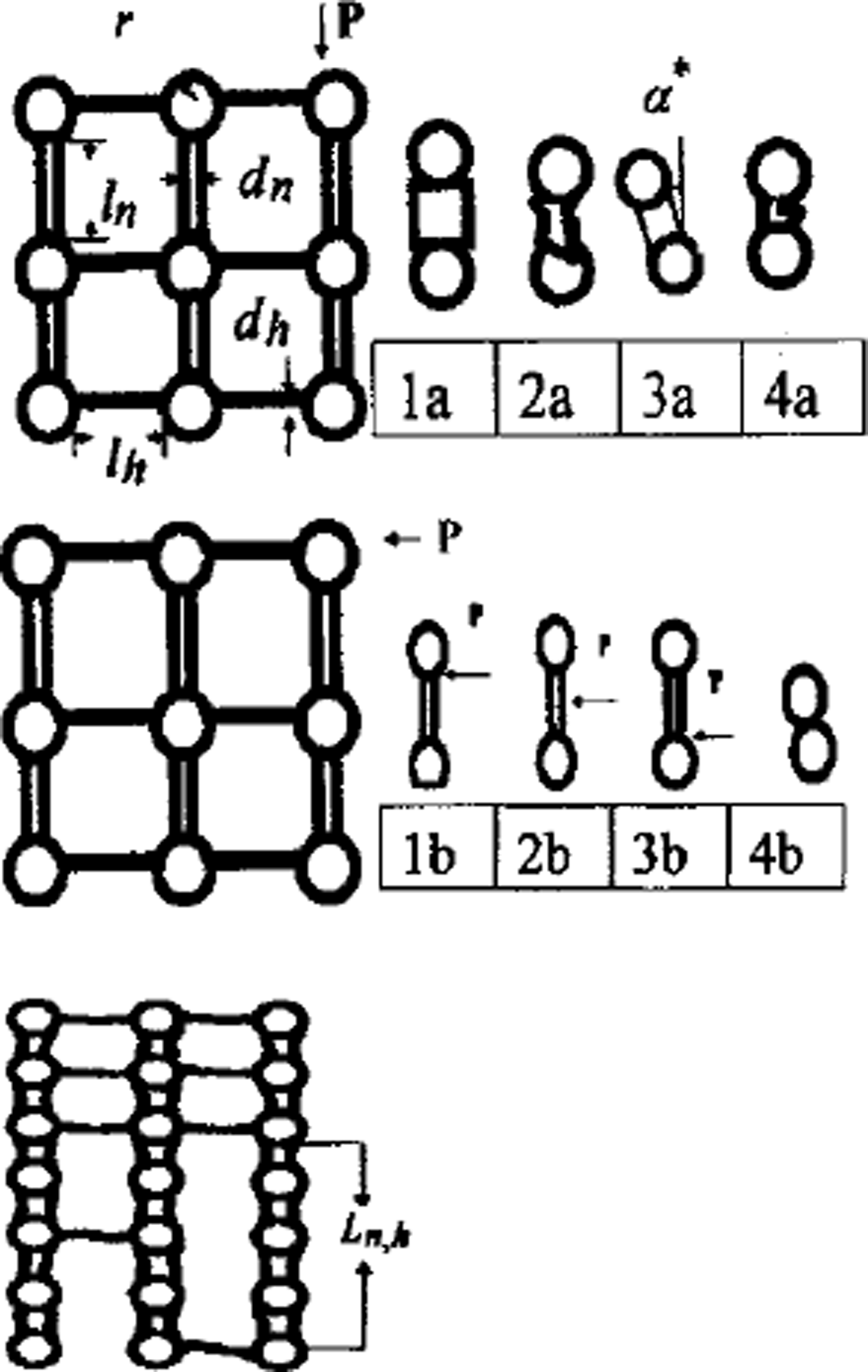
Fig. 2. Different variants of loading, (top, a) Vertical direction: la. viscoelastic deformation; 2a. compression; 3a. shear deformation; 4a. collapse, (middle, b) Horizontal direction: lb-3b. different variants of shear deformation; 4b. collapse. (bottom, c) Depth-hoar layer structure: P is the load; ln, lh are bond lengths; dn, dh are bond diameters; r is the grain radius. ln h is a common length of vertical bond chain, without horizontal bonds due to evaporation.
Depth hoar is often an important feature of the snowpack, and can be described in our model with the help of the structural-parameters variation and approximating heat and mass fluxes. The normal and horizontal bond diameters increase through the densification of snow and flow of the ice material. Anisotropic changes in normal and horizontal directions result from the flow under constant load and from evaporation of the bonds. For the snowpack-stability problem it is very important to know the location and thickness of the critical layers inside a snowpack. Calculating the structural and mechanical parameters in combination with the depth of critical layers makes it possible to estimate the avalanche volume.
Numerical Examples
Temperature, density, structural parameters and typical strength values within a snowpack were calculated using a mathematical model. A numerical finite-difference method has been used for simulations. For the calculation by this model the following initial data are necessary: air temperature, precipitation parameters, wind velocity and impulse parameters, air humidity, albedo, solar radiation, heat parameters and the initial density of the snow and soil. The meteorological parameters were updated every 12 hours. The data collected during 24 days in east Siberia (I) and during 16 days in central Asia (II) (Reference Golubev, Guseva, Voytkovskiy and DyurgerovGolubev and Guseva, 1987) were used for the present simulations and computations. The meteorological data ― air temperature, precipitation, layers and snow stratigraphy ― are shown in Figure 3a-c). Density, snow thickness and grain radii (initial, measured and calculated after 16 and 24 days) are given inTable 1 (cf Reference Golubev, Guseva, Voytkovskiy and DyurgerovGolubev and Guseva, 1987). The measured temperature fields (Fig. 3d) and measured thickness changes (Fig. 3e) during the calculation period were compared with calculated temperature field and thickness. As a result of snow metamorphism, the vertical orientation of crystals and the layers with low strength slowly appear. Formation of the depth-hoar horizons is connected with the strong mass transfer at the layer boundaries and the snow sublimation, with the column-structure formation and with formation of friable layers in the interior of the snowpack.
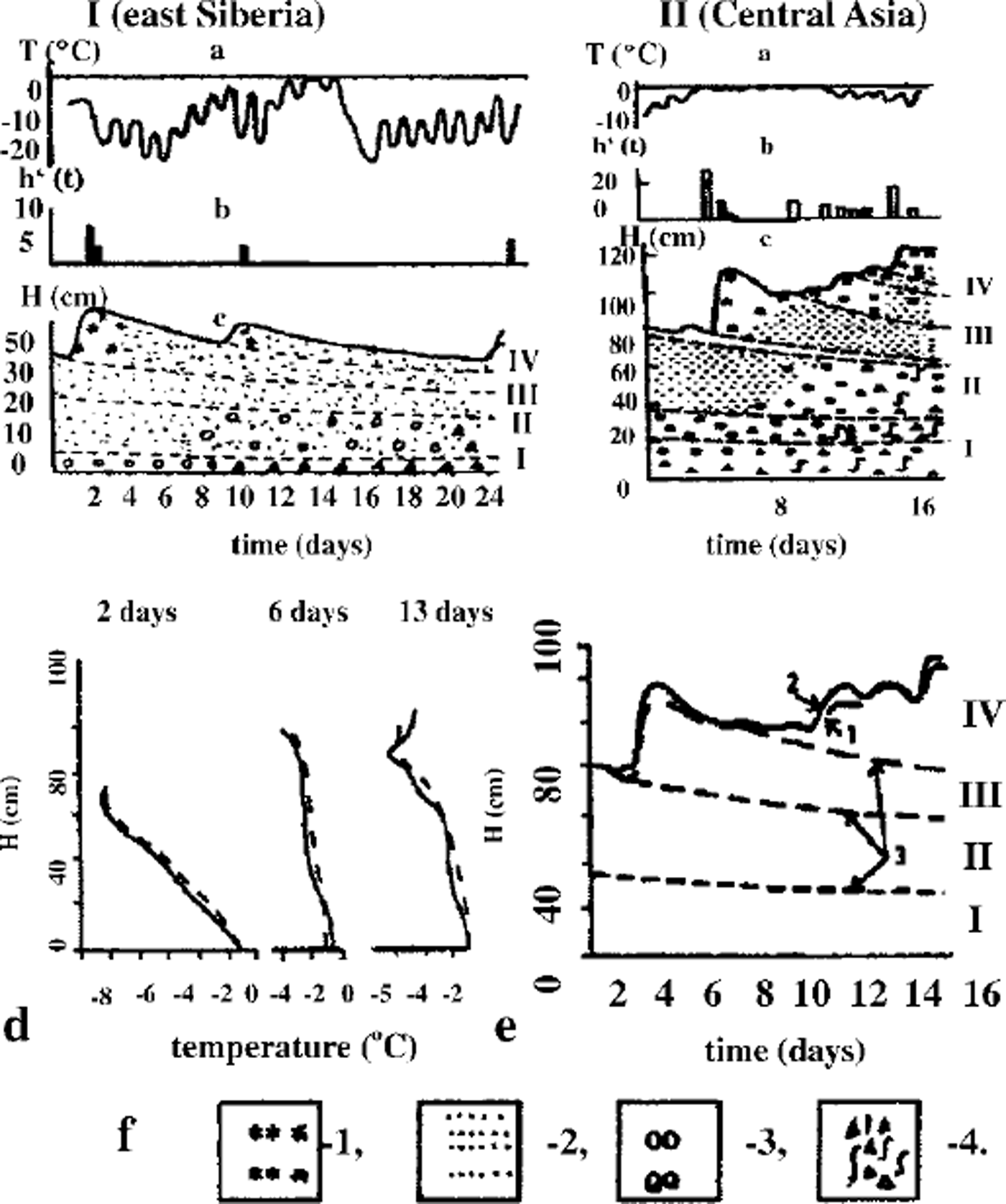
Fig. 3. Initial data collected (Reference Golubev, Guseva, Voytkovskiy and DyurgerovGolubev and Guseva, 1987) in (I) Udokan, east Siberia (October-November), and (IT) Chatkalskij, central Asia (February), (a) Air temperature; ( b) precipitation; ( c) snow depth and stratigraphy; Tis temperature, His snow thickness, h’(t) is precipitation, tis time in days, and I-IVare snowpack layers (see (c) and (e)); (d) Temperature distribution of the snow cover and ground (computed and observed); ( e) computed data of the snow depth compared to observed data; arrows indicate I observed data; 2 computed data; 3 boundary layers, (f) 1. Fresh snow; 2. fine grainedsnow; 3. coarse-grained snow; 4. depth hoar.
Table 1. Thickness (m), density (kgm–3) and grain radius (mm)
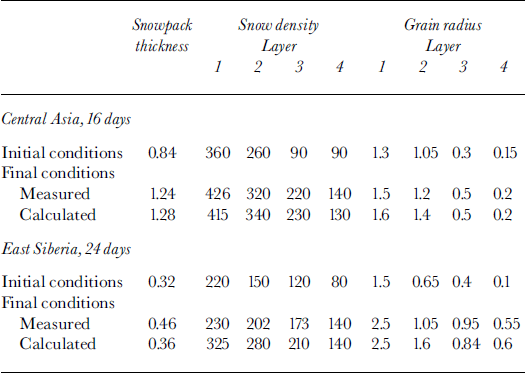
Computing the strength distribution inside the snowpack and assuming lower strength limits allows the snowpack stability to be estimated. The initial bond diameters dn,h = 2bn,hr and bond lengths ln,h = 2(kn,h–1)r were determined for different grain radii: 0.15 mm ≤ r ≤ 2.5 mm (according to the observations shown inTable 1 (Reference Guseva and GolubevGuseva and Golubev, 1989), for coefficients bn,h,kn,h: 0.05 ≤ δnh ≤ 0.25, kn,h6 ≈ 1.05 Snowpack thickness is ≤ 1.2 m The variation in average daily air temperature shown in Figure 3 and temperature in the upper snow layers is gradT ≤ 5°C m–1, due to the difference between daytime and nighttime temperatures. Snow-density variation is 90 kg m–3 <ρs< 450 kg m–3. Relative contact surface interval was calculated as 0.0004 ≤ σnh ≤ 0.024. Observations give the measured data of the compression strength: 0.12 ≤ n,h 6 ≤ 18kPa (Reference Golubev, Guseva, Voytkovskiy and DyurgerovGolubev and Guseva, 1987). The large spread in data can be explained by spatial inhomogeneity of the snowpack and slope morphology. The calculation periods for the real examples were 24 days (I) and 16 days (II). Different scenarios were calculated with initial conditions based on real examples I and II. Temperature distribution computed and observed is shown in Figure 3d for real example II. The depth changes during 16 days are shown in Figure 3e. The measured data and the calculated results are in fairly good agreement (see Fig. 3d and e). Figure 4 shows the calculated temperature isotherms for the different points of slope, β1 = 0° and β3 = 45°. The temperature fields are different due to different snow thickness. Figure 5 illustrates the mass transfer within the snowpack due to condensation and evaporation. The water-vapor concentration in porous space is shown in Figure 5a. Figure 5b and c show the density distributions of mass-transfer flux as the sum of sublimation and evaporation during 16 days for different snowpack thicknesses. The calculations show that at the layer boundaries and soil-snow boundary the mass transfer can reach essential values. The observations confirmed these results. Figure 6 illustrates the mass transfer inside the snowpack due to recrystallization. At the boundaries of each layer (contact of grains with different grain radius and structure parameters) and at the snow-ground boundary the mass-transfer process is essential (Fig. 6a). The difference between horizontal and vertical bonds is sufficient at these zones within the snowpack. The bond diameters are changed because of sublimation/ condensation processes in windless and windy conditions. Windy conditions accelerate the increase in normal bond diameters and the decrease in horizontal bond diameters. This process depends on the temperature, air moisture, windy densification and gust parameters. In Figure 6a two profiles of the normal and horizontal bond diameters are shown, with and without windpumping The influence of windpumping on structural and other parameters, temperature and strength is essential near the surface. The increase in bond diameters through windpumping leads to greater hardening of the ice-matrix elements and the formation of depth-hoar layers. This anisotropic trend was estimated by calculating coefficient × (Fig. 6b). Snowstorms and windy weather change the structural parameters within the upper part of snowpack through windpumping and windy densification. This changes the temperature and moisture distribution within the snowpack. The change in temperature and temperature gradient causes mass-transfer variation in the snowpack. Wind densification also intensifies heat and mass transfer in the lower snow layers. The snowstorm conditions were simulated using structural data fromTable 1 for central Asia. The difference in windpumping-influence depth between calculated data (Fig. 6) and those in Reference ColbeckColbeck (1997) can be explained by differences in initial density distribution, air temperature andwind rates. Decrease in horizontal bond diameters due to evaporation of the smaller structural elements leads to fracture of these bonds beneath overlying snow at the slope. The calculation of the example with initial conditions from Table 1, and based on the real example during 456 hours with weather and structural conditions (Fig. 3a), indicates that some layers of the interior snowpack failed (Fig. 7). The failure estimations of these layers were computed using Equation (7). We assumed that all bonds in these layers collapsed. The layer collapses and the thickness is reduced to the length of failed bonds.
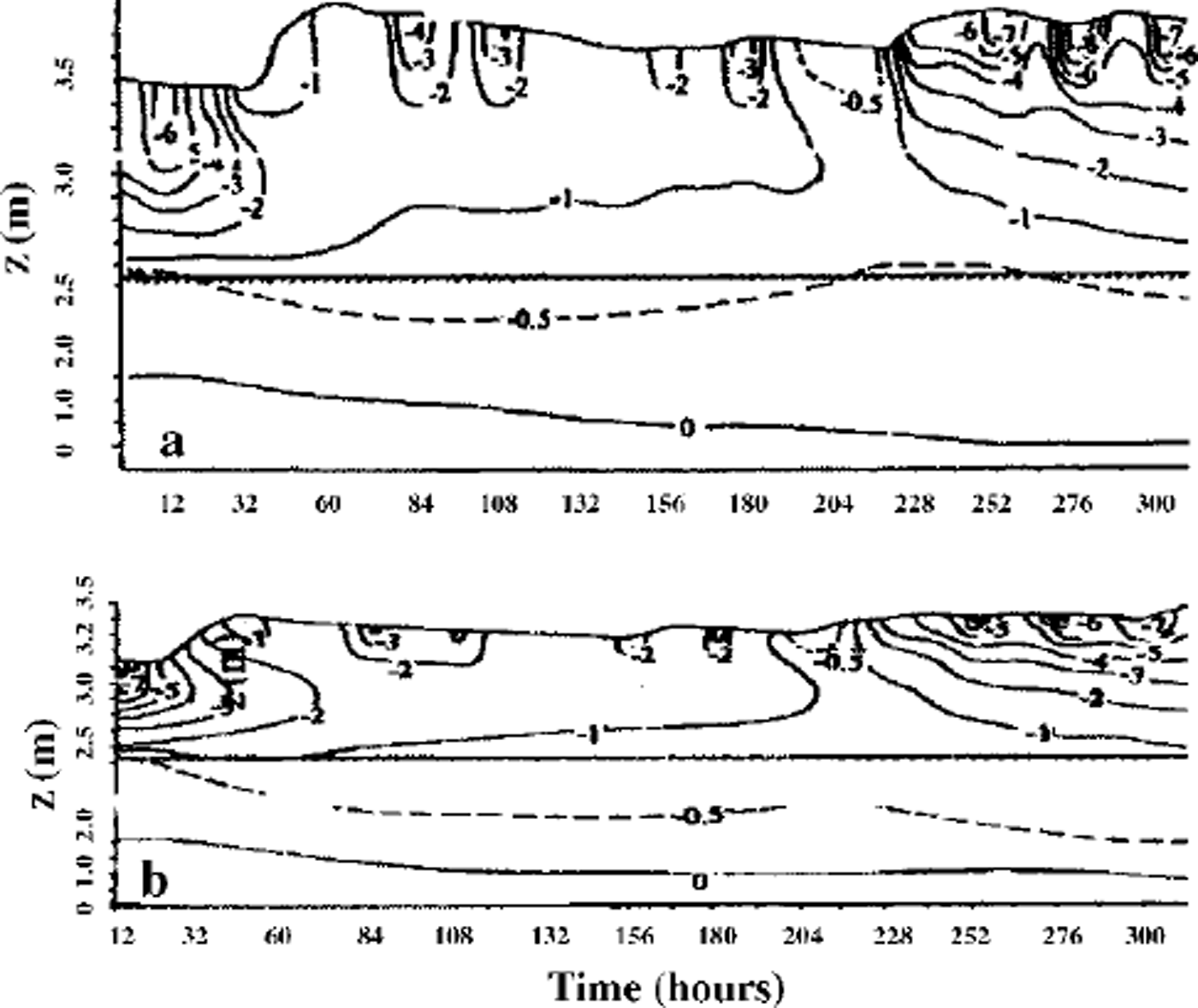
Fig. 4. Calculating isotherm fields for slope angle β1(x)=0°
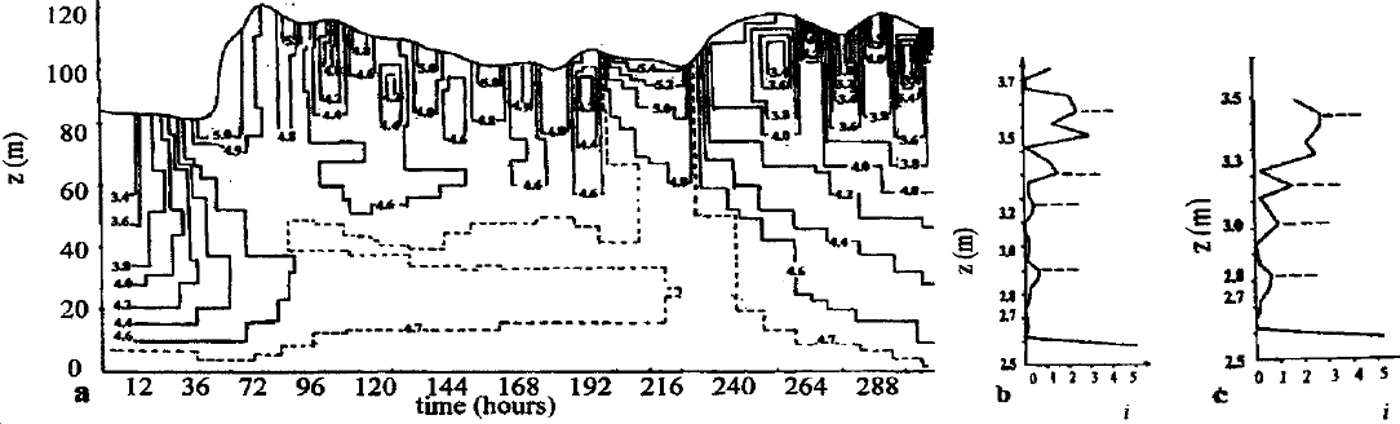
Fig. 5. Mass-transfer field within snowpack. (a) Water-vapor concentration field, (b) Density of mass-transfer flux (i = jx l0–4 kgm–2 hȡ1 ) during 14 days for slope point with angle β1=0° (see Fig. lb), (c) Density of mass-transfer flux (i = jx l0–4 kg m–2 hȡ1 ) during 14 days for slope point with angle β3 = 45° (see Fig. lb).
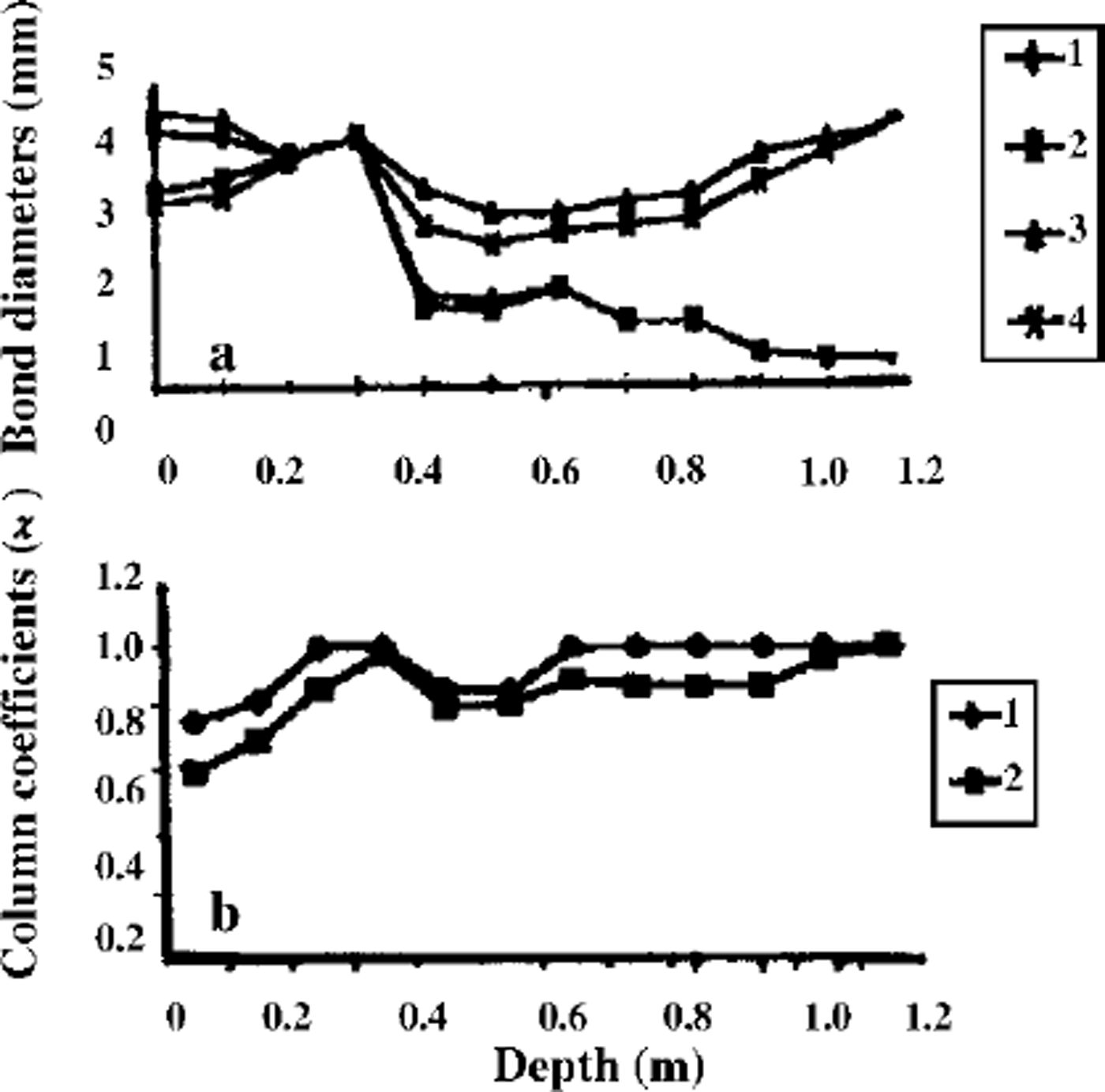
Fig. 6. Vertical and horizontal bond diameters in windless and windy conditions, (a) 1. dn;2 dh;3. dn;4. dh;J, 2 windless conditions; 3,4. windy conditions, (b) Column coefficients. 1. Xfor windless conditions; 2. xfor windy conditions.
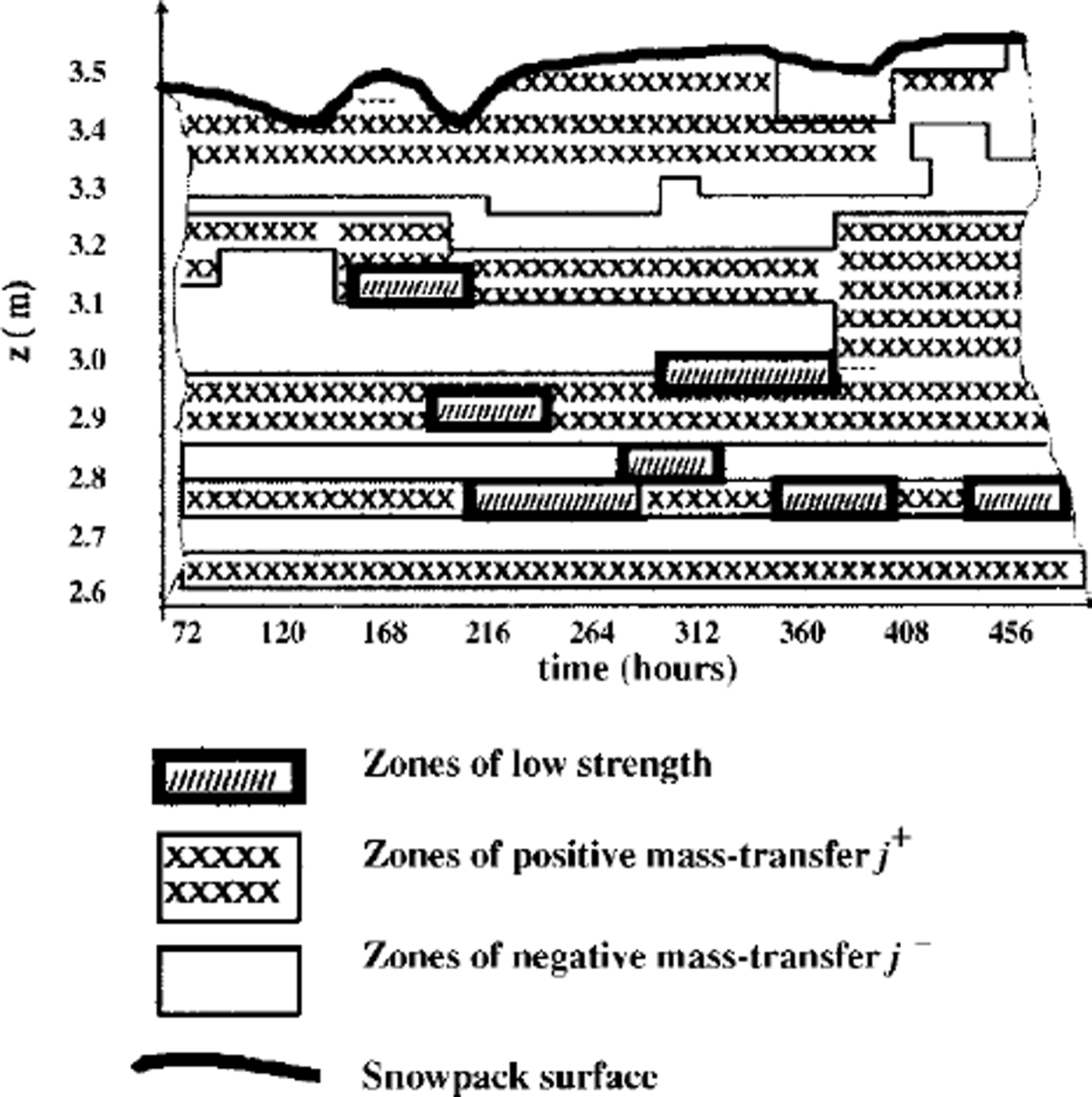
Fig. 7. The mass-transfer field with zones of low strengths inside of snowpack. Calculation time was 456 hours.
Conclusion
It is necessary to know layer boundary locations inside the snowpack because they can be potential avalanche sliding surfaces. Computing of the snow properties may be useful for avalanche forecasting. The mathematical and numerical heat- and mass-transfer model has been developed and may be used for avalanche prediction and monitoring snowpack stability, to estimate the time and position of depth-hoar zones formation and to calculate the snow strength in different snowpack layers and its variation by metamorphic processes.










