Introduction
Contrary to perennial ice pack covering the central Arctic Ocean, seasonal sea ice is relatively thin and has lower mechanical strength, and is therefore easily fragmented into separate floes. Whereas compact ice cover can be successfully modeled as a continuous medium (with various versions of a viscous-plastic or, recently, elasto-brittle rheology), at ice concentrations A < 1 the ‘macroscopic’, large-scale dynamics of ice is a complex, emergent result of ‘microscopic’ processes taking place at a floe level. Ice cover composed of separate floes constitutes an example of a very complex granular medium, composed of particles - ice floes - interacting with each other and with the surrounding ‘interstitial’ fluids (air and water) via a number of mechanisms. One of the most crucial (and computationally challenging) properties of that granular material is its very strong poly-dispersity. The observed floe-size distributions (FSD) are heavy-tailed, typically of power-law type (although other distributions (e.g. from the Weibull family) have also been proposed) with an exponent a < 2 (e.g. Reference Toyota, Takatsuji and NakayamaToyota and others, 2006, Reference Toyota, Haas and Tamura2011; Reference Steer, Worby and HeilSteer and others, 2008; Reference HermanHerman, 2010). In combination with a floe-size-dependent response to the external forcing, this strong variability of floe sizes contributes to the complex character of sea-ice dynamics, typical for seasonal ice and the marginal ice zone (MIZ). Selected aspects of that behavior have recently been numerically analyzed by Reference HermanHerman (2011, Reference Herman2012), in studies that concentrated on floe-cluster formation and collision patterns in sea ice.
In this work, the simple hard-disk model developed by Reference HermanHerman (2011, Reference Herman2012) is reformulated in a more general, easily extendable form, and its simplistic, computationally inefficient collision scheme is replaced with a more realistic floe/floe interaction model, based on Hertzian contact mechanics. As previously, sea ice is modeled as a two-dimensional (2-D) granular material composed of disk-shaped, inelastic ‘particles’ (floes) with a power-law size distribution, moving on the sea surface under a prescribed external forcing. Numerically, the model is based on the LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) library, and allows systems with thousands of particles within a model domain subjected to various types of deformation (convergence, shear, etc.) to be simulated.
This paper concentrates on patterns of forces (force networks) between ice floes, and the corresponding internal stress in ice subject to selected types of external forcing: pure convergence without wind; constant wind forcing at a constant ice concentration, without large-scale strain; and a simplified MIZ with constant wind forcing at an acute angle to the ice edge. The results are analyzed in the context of phenomena known from other types of polydisperse granular materials. They provide interesting clues for formulating models parameterizing internal stress in fragmented ice cover.
Molecular-Dynamics Sea-Ice Model
Let us consider an ensemble of N disk-shaped ice floes with a constant density,
p
, and with variable thickness, hi
, and radii, ri
, for i
= 1, . . . , N. The motion of the floes on the sea surface (assumed 2-D) is influenced by (1) the external body and surface forces and (2) the floe/floe interaction forces. In the following,
![]() and
and
![]() denote density of the surface and body forces, measured in N mr2 and Nmr3, respectively. The floe/floe interaction force,
denote density of the surface and body forces, measured in N mr2 and Nmr3, respectively. The floe/floe interaction force,
![]() , results from inelastic collisions of the floes. For two floes, i and j,
, results from inelastic collisions of the floes. For two floes, i and j,
![]() is nonzero if and only if those two floes are in contact. Let
is nonzero if and only if those two floes are in contact. Let
![]() denote the set of all floes in contact with floe i at a certain time instant, t. It is useful to express the force between i andj as a sum of two components, normal and tangential to the plane of contact, denoted as
denote the set of all floes in contact with floe i at a certain time instant, t. It is useful to express the force between i andj as a sum of two components, normal and tangential to the plane of contact, denoted as
![]() and
and
![]() , respectively.
, respectively.
![]() contributes to the translational motion of floes i and j, and
contributes to the translational motion of floes i and j, and
![]() to their rotation.
to their rotation.
Momentum equations for ice floes
The general form of the linear momentum equation of the ith floe is (e.g. Reference LeppärantaLepparanta, 2005):
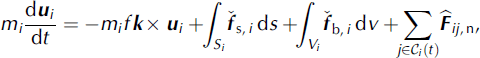
where
![]() is the mass of the floe,
u
i
is the velocity of its mass center, t is time, f is the Coriolis parameter,
k
is a unit vector pointing vertically upward and Si and Vi are the surface and volume of the floe. Analogously, the angular momentum equation can be written as
is the mass of the floe,
u
i
is the velocity of its mass center, t is time, f is the Coriolis parameter,
k
is a unit vector pointing vertically upward and Si and Vi are the surface and volume of the floe. Analogously, the angular momentum equation can be written as
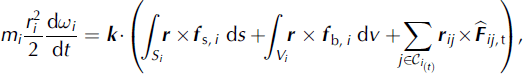
where wi denotes the angular velocity of floe i, r the distance from the floe’s center and r ij a vector pointing from its center to the contact point with floe j.
External forcing acting on the floes
In this work it is assumed that there are no external body forces
![]() and that four terms contribute to the total surface forcing,
and that four terms contribute to the total surface forcing,
![]() :
:
The atmospheric and oceanic skin drag, τ
ha,i
and τhw,i, act on the upper and lower surface of the floe, respectively (with surface area of both equal to πi
2
). The atmospheric body drag, τva, i, acts on the floe’s edges above the waterline and, in the case of deformed ice, on the slopes of ridges. Here we assume that the vertical area exposed to τvai
equals πrihf
i
, where
![]() is the floe’s freeboard and ρw
is water density. Analogously, the oceanic body drag, τνw, i, acts on the floe’s edges below the waterline and on the slopes of keels, and the area exposed to it equals π
ri
(
hi
-
hfi).
is the floe’s freeboard and ρw
is water density. Analogously, the oceanic body drag, τνw, i, acts on the floe’s edges below the waterline and on the slopes of keels, and the area exposed to it equals π
ri
(
hi
-
hfi).
The terms on the right-hand side of Eqn (3) are calculated as
where ρa denotes the air density, u a and u w are the wind and current velocities, respectively, and C ha, C hw, C va and C vw are drag coefficients at the horizontal and vertical surfaces of the floe.
Thus, the final form of Eqns (1) and (2) is (see also Reference LeppärantaLepparanta, 2005):
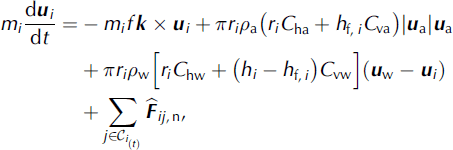
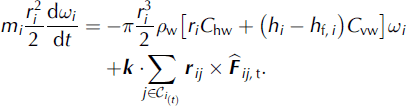
As analyzed by Reference HermanHerman (2011, Reference Herman2012) (for a simplified case without the Coriolis force and without rotational motion of the floes), the response of the floes to the forcing is size-dependent, with larger floes generally having larger equilibrium velocity directed at wider angles to the wind, and reacting more slowly to changes in forcing. In situations with wide, heavy-tailed floe-size distributions, this fact is responsible for a number of important phenomena, including formation of force networks at concentrations below the jamming transition, discussed in this work.
Floe/floe contact mechanics
Each of the normal and tangential forces,
![]() , and
, and
![]() in Eqns (6) and (7) is a sum of two terms:
in Eqns (6) and (7) is a sum of two terms:
The two normal forces are the Hertzian contact force
![]() and the damping force
and the damping force
![]() . Analogously, the components of the tangential force are the shear force
. Analogously, the components of the tangential force are the shear force
![]() and the damping force
and the damping force
![]() . According to Hertzian mechanics, the forces between the interacting objects depend on the distance, 8, between their edges: the forces equal zero for δ ≤ 0 and increase proportionally to δ ≤ 9 for 8 < 0. Details of the Hertzian model in a general context are given by, for example, Reference Brilliantov, Spahn, Hertzsch and PoschelBrilliantov and others (1996), Reference Zhang and MakseZhang and Makse (2005), Reference SchwagerSchwager (2007) and Reference ZhouZhou (2011). In sea-ice studies, (elements of) this model were used, for example, by Reference Hopkins and ThorndikeHopkins and Thorndike (2006) and Reference Fortt and SchulsonFortt and Schulson (2011). From the point of view of this study, the Hertzian contact model has two advantages. Firstly, it is suitable for polydisperse systems and, secondly, the coefficients in the formulations of the terms of Eqn (8) are functions of well-defined material properties of the particles (in this case, sea ice). The material properties of sea ice used in the simulations were obtained by Reference SchulsonSchulson (1999).
. According to Hertzian mechanics, the forces between the interacting objects depend on the distance, 8, between their edges: the forces equal zero for δ ≤ 0 and increase proportionally to δ ≤ 9 for 8 < 0. Details of the Hertzian model in a general context are given by, for example, Reference Brilliantov, Spahn, Hertzsch and PoschelBrilliantov and others (1996), Reference Zhang and MakseZhang and Makse (2005), Reference SchwagerSchwager (2007) and Reference ZhouZhou (2011). In sea-ice studies, (elements of) this model were used, for example, by Reference Hopkins and ThorndikeHopkins and Thorndike (2006) and Reference Fortt and SchulsonFortt and Schulson (2011). From the point of view of this study, the Hertzian contact model has two advantages. Firstly, it is suitable for polydisperse systems and, secondly, the coefficients in the formulations of the terms of Eqn (8) are functions of well-defined material properties of the particles (in this case, sea ice). The material properties of sea ice used in the simulations were obtained by Reference SchulsonSchulson (1999).
The numerical model
Replacement of the hard-disk approach used by Reference HermanHerman (2011, Reference Herman2012) by the more advanced collision model described at the start of this section has some very important (predominantly positive) consequences for the numerical implementation of the model. Whereas hard-disk algorithms progress from one collision to the next, which makes them extremely computationally expensive in situations with high collision rates, the present approach allows the use of a constant time-step, Δt, limited by the characteristic collision duration in the analyzed system. Thus, the model run times are, firstly, predictable and, secondly, to a large degree independent of the details of a particular model configuration.
The numerical model has been built based on the LAMMPS library (Reference PlimptonPlimpton, 1995; http://lammps.sandia. gov/), one of the classical molecular dynamics programs, designed for large systems of particles interacting through a variety of short- or long-range forces. The code is highly parallel, based on neighbor lists and effective spatial decomposition techniques. For the purpose of this work, LAMMPS has been extended to disk-shaped particles in 2-D domains. For all N particles, the Newton equations of motion, Eqns (6) and (7), are solved by means of the velocity-Verlet integrator.
A list of the model parameters used in the simulations is given in Table 1.
Table 1. Physical and numerical model parameters used in the simulations
Contact and Force Networks
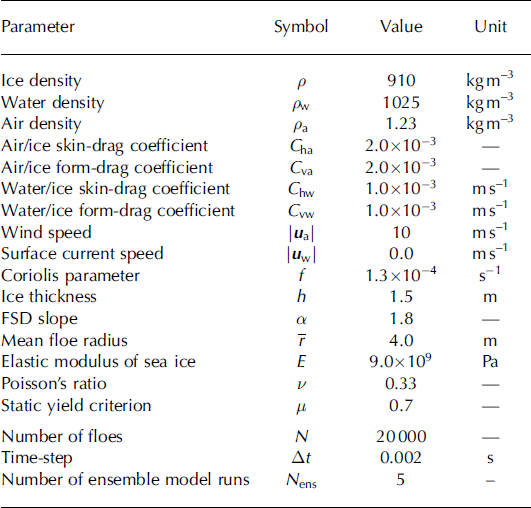
Global, large-scale properties of granular materials can be characterized by a number of measures. From the point of view of this work, two very useful properties are the contact fabric tensor and the stress tensor. The contact fabric tensor, R, is defined as an average vector outer product of unit normal vectors at contact between particles within a given domain (Reference Madadi, Tsoungui, Latzel and LudingMadadi and others, 2004; Reference Zhang, Majmudar, Tordesillas and BehringerZhang and others, 2010; Reference Bi, Zhang, Chakraborty and BehringerBi and others, 2011; Reference Shaebani, Madadi, Luding and WolfShaebani and others, 2012). According to the formulation used by Reference Zhang, Majmudar, Tordesillas and BehringerZhang and others (2010), suitable for disk-shaped particles:
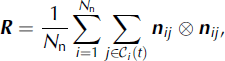
where n ij = r ij/| r ij | is a unit normal vector pointing from the center of disk i to the contact point with disk j and N n is the number of floes with at least two contacts (called ‘non-rattler grains’). The fraction of non-rattler grains is denoted fnr = N/N Reference Bi, Zhang, Chakraborty and BehringerBi and others (2011) showed that f nr controls phase transitions in sheared granular materials. The average contact number per particle, ηc, and the measure of anisotropy of the contact network, ηa, can be obtained from the eigenvalues of R , λ 1 and λ2, as ηc = λ1 + λ2 and λ2, as ηc = λ1 + λ2.
Analogously, the stress tensor, σ, is defined as:
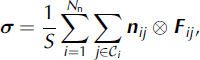
where S denotes the surface area of the system and F ij is the sum of terms in Eqn (8). The pressure, p, and shear stress, τ, can be obtained from the principal stresses, σ 1 and σ 2, as p=(σ1+σ2)/2 and σ1=σ2.
Whereas the interpretation and usage of the stress tensor, σ, are well established in numerical modeling of sea ice, the meaning of tensor R requires some explanation. In granular materials subject to external stresses, grains form (generally inhomogeneous) contact networks and the external load is carried by so-called force chains: elongated, filament-like structures built of linearly arranged grains touching their neighbors. The response of a granular material to a particular type of deformation (shear, compression, etc.) depends on the statistical measures of the force network; ηc and ηa are among the most basic measures, describing its stability and anisotropy. For example, a regular ‘mesh’ of identical, densely packed disk-shaped particles has ηc = 6 (each particle has six neighbors arranged around its perimeter) and ηa = 0 (there is no asymmetry in the structure of the contact network). Simple stability arguments show that ηc ≥ 3 is necessary for a granular material to be able to resist stress (to stabilize the position of a given grain, it has to be ‘held in place’ by at least three neighbors). The values of ηa > 0 indicate that the force chains are arranged in a preferable direction, and that the ‘stiffness’, or strength, of the material along that direction is higher than in other directions.
Modeling Results
Jamming phase transition in pure convergence
Before we proceed to more complex situations, it is useful to analyze the time evolution of a system of floes subjected to pure convergence, without wind. As we will see below, this scenario allows us to define two clearly separated regimes, or states, of sea ice.
Figure 1a shows the evolution of the internal pressure, p, with increasing ice concentration, A. Initially, floe/floe collisions are sporadic, and the corresponding levels of internal stress are close to zero. Increasing A leads to decreasing floe/floe distances and higher collision rates. The relationship between p and A is approximately exponential, until a certain limiting value of A, denoted AJ, is reached, marking the onset of a rapid, hyperexponential increase of pressure. As in other granular systems (Reference Pica Ciamarra, Nicodemi and ConiglioPica Ciamarra and others, 2010), the exact numerical value of AJ depends on the geometrical and material properties of the particles (in this case, exponent a of the FSD, which determines the packing efficiency of floes on the sea surface, and the elastic and damping coefficients that influence the repulsive force between interacting floes), as well as on the path along which the system is driven towards the jammed state. However, in the analyzed cases the value of A J was found to be relatively stable, between 0.918 and 0.921. It is worth noting that, due to the high packing efficiency of floes with wide size distributions, AJ is higher than typically obtained in monodisperse granular materials.
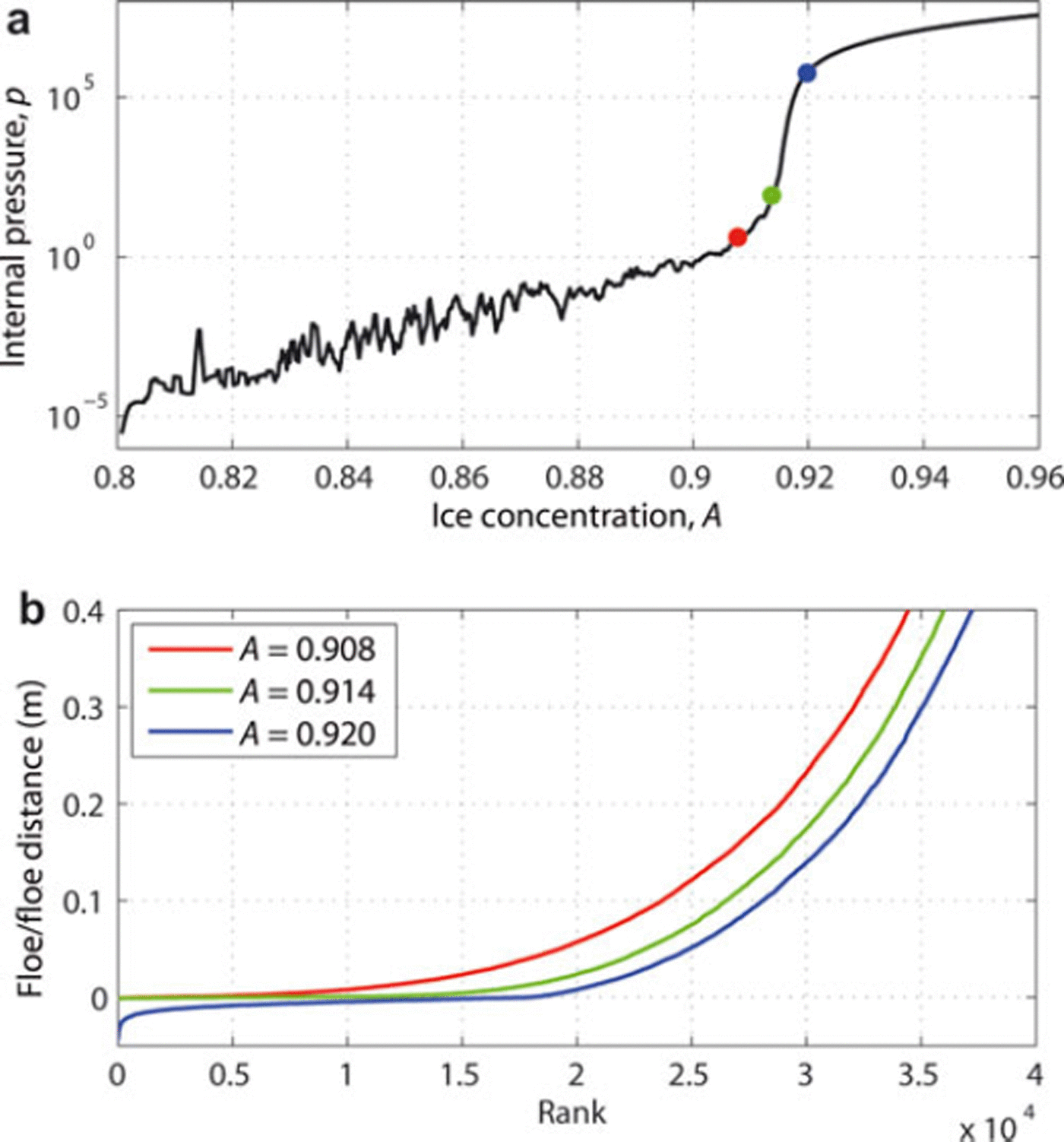
Fig. 1. Jamming transition in sea ice under pure convergence for dA/dt = 0.04 h–1: (a) evolution of pressure, p(A); (b) rank-order distribution of floe/floe distances, 6, below and above AJ, in the three situations marked with dots in (a).
Qualitative differences between the states below and above AJ manifest themselves in marked differences in properties of the networks of contact forces between the floes. Before the onset of jamming, there is still enough free space that the repulsive forces generated during collisions make it impossible for permanent floe/floe contact to develop. Snapshots of the unjammed system show forces only between pairs of floes undergoing a collision at that particular time instant (Fig. 2a). Accordingly, floe/floe distances tend to be small, but larger than zero (Fig. 1b), the mean contact number η c ≈ 1 (binary collisions) and the non-rattler fraction f nr ≈ 0 (Fig. 3). When the system approaches AJ, formation of ‘clusters’ of floes with larger numbers of neighbors (Fig. 2b) leads to increasing p, η c and fnr. At AJ, the force network percolates the whole system (Fig. 2c), the distances between a large number of neighboring floes drop to zero (Fig. 1b) and r] c exceeds 3, which is the minimum value necessary to stabilize the positions of the floes (the number of neighbors of individual floes is roughly proportional to their perimeters). Obviously, under pure convergence η a and τ remain close to zero (not shown).

Fig. 2. Simulated distribution of instantaneous forces between ice floes under pure convergence, at A equal to (a) 0.908, (b) 0.914 and (c) 0.920, i.e. in situations corresponding to those marked with dots in Figure 1. For each floe i, a line is drawn from its center to the center of floe j=Ci(t). For clarity the plots show only fragments of the modeled system.
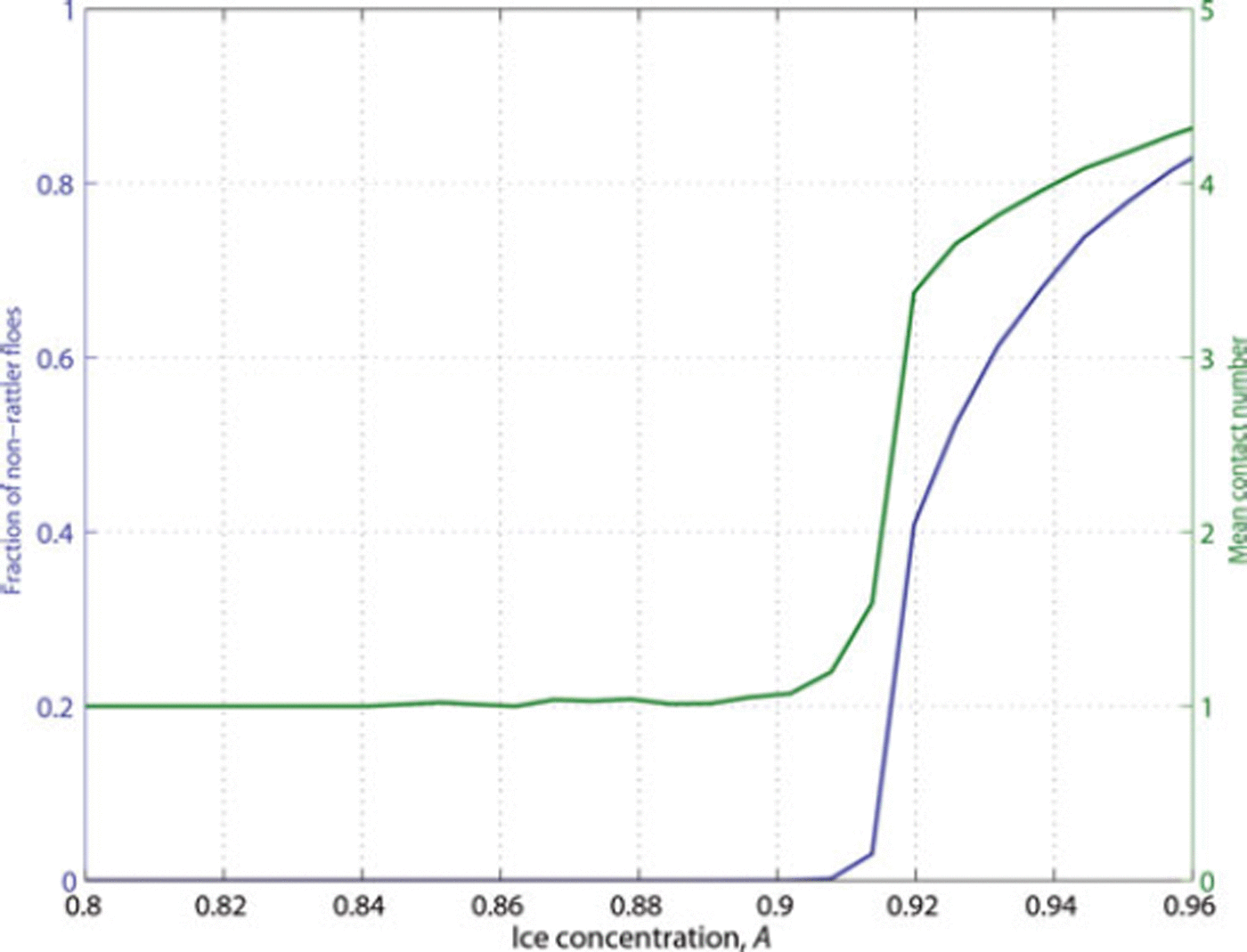
Fig. 3. Evolution of the mean contact number, η c, and the fraction of non-rattler floes, fnr, with ice concentration, A, during the pure-convergence simulation.
The jamming transition thus separates two very different regimes. Below AJ, in the unjammed state, floe/floe collisions are the dominant source of the internal stress. Moreover, because the floes have some space to move independently of their neighbors, the size-dependent response of individual floes to external forcing plays an important role in the macroscopic behavior of sea ice (Reference HermanHerman, 2011, Reference Herman2012). Above AJ, owing to the existence of a system-size force network, the ice possesses a certain stiffness, or robustness, and can resist certain levels of stress without undergoing irreversible deformation. (Of course, the results become unrealistic at some A 3> AJ, when the load exceeds the ice strength and the floes break, raft on top of each other, etc.)
It is worth noting that even in the jammed state, the fraction of force-bearing floes, fnr, is still much lower than 1 (Fig. 3). The percolated force network has an openwork structure, with patches of unjammed (usually relatively small) floes surviving among force-bearing floes up to A far above AJ (Fig. 2c). The consequences of this force-network property on point measurements of stress in the ice are briefly discussed in the final section.
Force networks under uniform wind
In order to illustrate the role of the size-dependent response of the ice floes to external forcing, let us analyze a simple case of ice under a uniform wind with ua=10ms1 and a constant ice concentration, A (varied between model runs). The simulations presented below were performed within square domains with periodic boundaries. Tests with other types of boundary conditions and in domains of different sizes showed that the results were not sensitive to the formulation of the boundary conditions.
Snapshots of the system in a quasi-equilibrium state for two selected values of A (Fig. 4) show that wind-forced sea ice has features resembling those present in the transitional phase preceding the jamming transition in the case analyzed above (Fig. 2b). Although the force networks do not percolate the entire model domain, ‘locally jammed’ subregions develop with above-average density of the contact and force networks. The similarity manifests itself in the values of pressure (cf. Figs 5a and 1a) and r] c (Figs 5b and 3). However, in many ways the wind-forced scenarios are different from the pure-convergence case. Importantly, with decreasing A and increasing role of the size-dependent response of individual floes, the force and contact networks become more localized and more asymmetric. For A<∼0.84, characteristic bands of densely packed floes develop, with higher-than-average p and rj c, separated by regions of locally lower ice concentration and sporadic, binary collisions (Fig. 4a). Contrary to the convergence case, the system has significant values of the shear stress, r, and anisotropy, ?] a (Fig. 5), which increases with decreasing A (from almost zero at A = AJ). Thus, wind-forced sea ice possesses some features resembling the shear-jammed states in 2-D granular materials, described by Reference Zhang, Majmudar, Tordesillas and BehringerZhang and others (2010) and Reference Bi, Zhang, Chakraborty and BehringerBi and others (2011).

Fig. 4. Simulated distribution of instantaneous forces between ice floes subject to a constant wind with uax = 10ms_1 and uay = 0, at A equal to (a) 0.82 and (b) 0.90. For clarity, the plots show only fragments of the modeled system.

Fig. 5. Statistical measures of the force and contact networks in simulations with constant wind: (a) pressure, p, and shear stress, r; (b) mean contact number, rj c; and (c) anisotropy measure, ηa.
Force networks in a marginal ice zone
Finally, a set of simulations representing a simplified MIZ was performed, assuming that the floes along the lower boundary of the model domain, representing the fast-ice edge, are stationary (‘frozen’). Periodic boundary conditions were applied to the left and right boundaries. As previously, the wind velocity ua=10ms1 in all simulations; the wind direction relative to the ice edge was kept constant in each individual model run, but varied between simulations. All simulations were performed until a quasi-stationary state was reached.
The modeled across-ice-edge (y-direction) profiles of along-ice-edge ice velocity, ux(y), are similar to those produced by other models (Reference FelthamFeltham, 2005). At first, ice velocity changes smoothly across the width of the MIZ, but this stage is short-lived. The final velocity profile is characterized by a narrow region of strong velocity gradients, separating stationary ice adjacent to the model boundary from the outer zone, moving with an approximately constant speed, dependent on the alongshore wind velocity (Fig. 6). It should be noted that the motionless inner zone is not limited to the floes arbitrarily declared as ‘frozen’, but extends into the MIZ and comprises a strip of jammed floes.
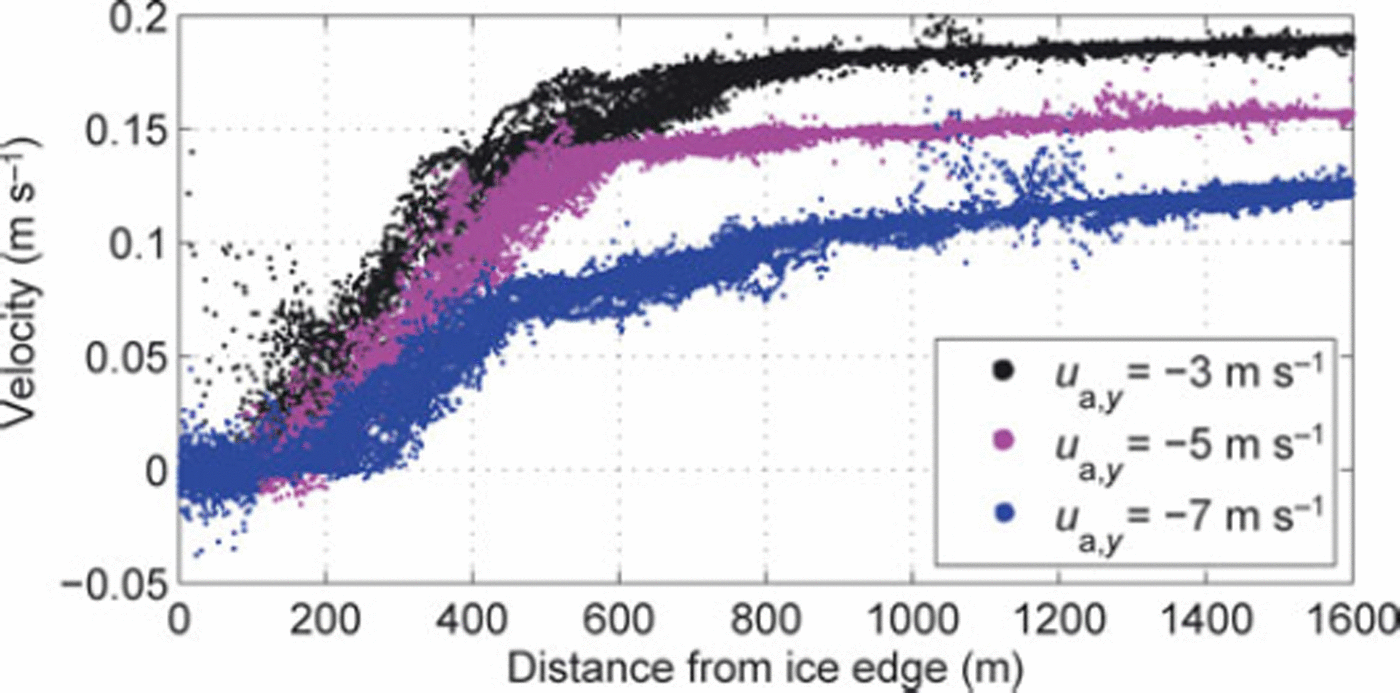
Fig. 6. Along-ice-edge ice velocity of individual floes, u, x(y), simulated with three different wind directions (in all cases, ua=10ms and ua,y denotes the cross-shore component of u a).
Probably one of the most striking features of the model behavior is the erratic character of the internal stress. Although many general, global characteristics of the modeled MIZ remain stable in time, the area-averaged stress undergoes irregular changes, with uneven cycles of stress build-up and sudden drops (Fig. 7), corresponding to localized jamming events. Unloading of jams can also be seen in Figure 6: during local rearrangements of floes some of them (usually smaller ones) acquire speeds larger than the equilibrium speed corresponding to their position within the MIZ. Importantly, as shown in Figure 7b, although the changes of p and τ are correlated (with a correlation coefficient of 0.68), their instantaneous ratio varies considerably from close to 1 up to ∼12.
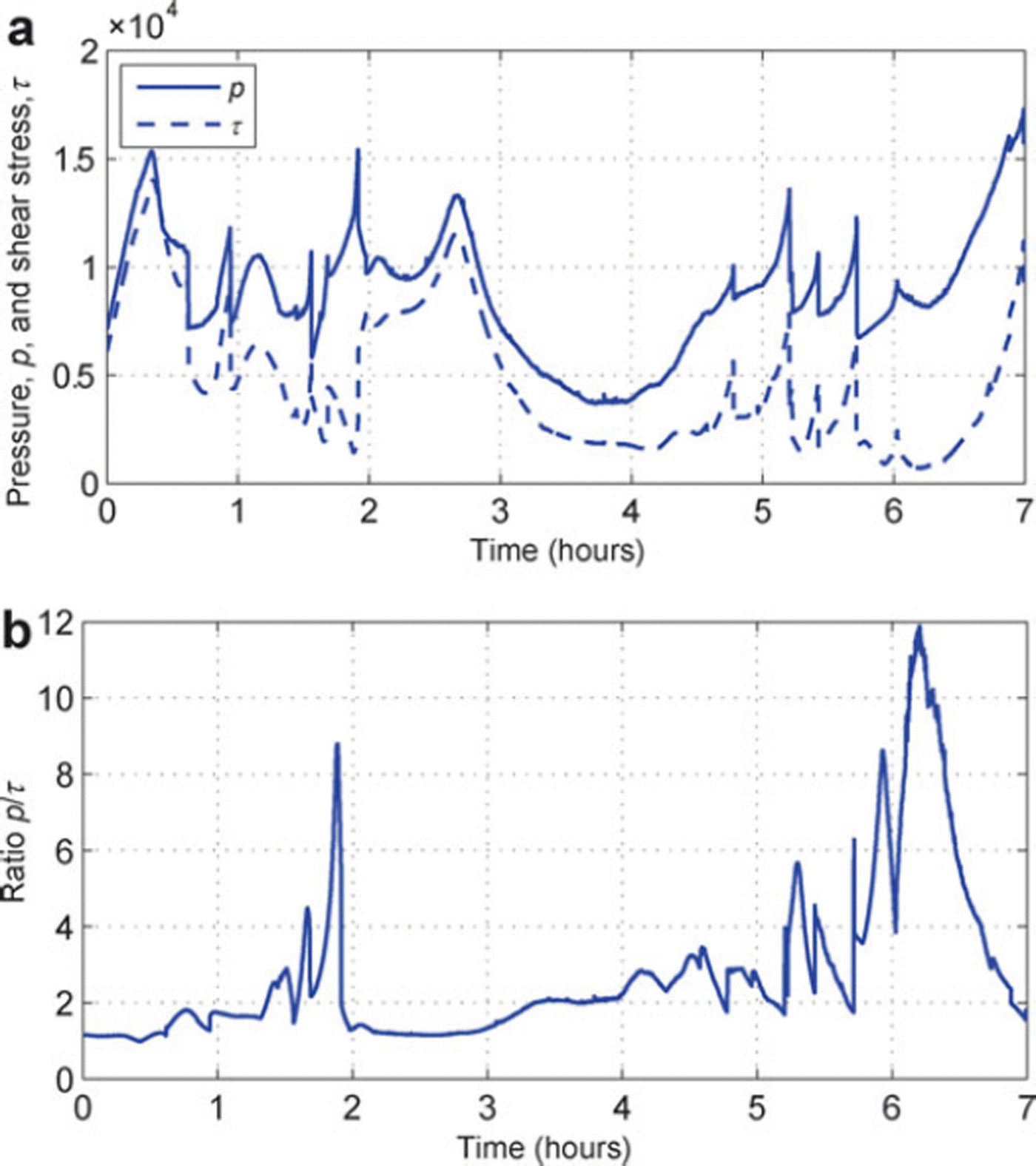
Fig. 7. (a) Fragments of simulated time series of pressure, p, and shear stress, r, and (b) their ratio, p/r, in the MIZ under stationary wind forcing (ua=10ms1 and uay=5ms)
Interestingly, the pressure levels, although more than two orders of magnitude higher than in the simple wind-forced cases analyzed above, still remain within the range corresponding to the transitional regime just below AJ (Figs 7 and 1a). Also, independently of the wind direction, nc=1.6 statistical properties of the contact networks remain relatively stable in all analyzed cases. Importantly, they are not sensitive to details of the model configuration. In particular, changes in the material properties of the ice (provided that they remain within reasonable limits) influence the model behavior in the initial phase of the simulations, but their significance is very limited after a dynamic equilibrium is reached under a specified forcing.
Finally, it is worth noticing that the MIZ simulations described above were initialized with floes having random positions and sizes drawn from a single, prescribed FSD (Table 1), whereas in real-world MIZs the average floe size and the shape parameters of the FSD depend on the distance from the ice edge (e.g. Reference Lu, Li, Zhang and DongLu and others, 2008; Reference Toyota, Haas and TamuraToyota and others, 2011). In the idealized cases analyzed here, if the simulations are carried out for a sufficiently long time, the largest/smallest floes tend to migrate towards the inner/outer sections of the MIZ, suggesting the existence of an inherent sorting mechanism transferring largest floes to regions of lower average flow velocities (although I do not suggest that a similar mechanism is responsible for the observed changes of the FSD properties across MIZs).
Discussion and Conclusions
One of the most important conclusions from this work concerns the irregular, ‘unpredictable’ character of stress in fragmented sea ice. The simulations show that even in idealized situations with constant forcing, internal stress has very high spatial and temporal variability. Moreover, this variability manifests itself at various spatial scales, from individual floes up to much larger sub-regions in the ice cover. Due to the openwork nature of force networks in sea ice, even a compact ice cover consists of force-bearing and ‘free’ floes with very different stress levels. Lower ice concentrations favor formation of patches of relatively high stress among more loosely packed floes. In MIZ simulations, even the domain-averaged stress undergoes erratic fluctuations with high magnitude. This aspect of the modeling results is in agreement with the results of point measurements of stress in sea ice, which demonstrate low correlation between stress measured at neighboring locations (e.g. Reference Richter-Menge, McNutt, Overland and KwokRichter-Menge and others, 2002).
Another important aspect of the results presented in this study is that, if we allow for a size-dependent response of ice floes to the forcing, the system maintains a certain level of internal stress, even under uniform forcing. This behavior is qualitatively different from that predicted by the existing collisional rheology models (Reference Shen, Hibler and LeppärantaShen and others, 1984, Reference Shen, Hibler and Leppäranta1986; Reference Lu, Larsen and TrydeLu and others, 1989). Due to unrealistic assumptions that all ice floes are uniformly distributed on the sea surface, and that they react to the forcing in the same way, those models predict nonzero internal stress in sea ice only if the forcing is spatially nonuniform, i.e. under macroscopic strain of the floe field. In view of deficiencies of existing collisionalrheology parameterizations, the model formulated here provides a valuable starting point for formulating more reliable rheology models, suitable for fragmented sea ice with variable concentrations.
Acknowledgements
This work was supported by European Union research grant No. POIG.01.01.02-22-011/09-00 (‘SatBaltic’). I am grateful to the two anonymous reviewers for their insightful and valuable comments and suggestions on the first version of the manuscript.









